Java并发包源码学习系列:阻塞队列实现之PriorityBlockingQueue源码解析
系列传送门:
- Java并发包源码学习系列:AbstractQueuedSynchronizer
- Java并发包源码学习系列:CLH同步队列及同步资源获取与释放
- Java并发包源码学习系列:AQS共享式与独占式获取与释放资源的区别
- Java并发包源码学习系列:ReentrantLock可重入独占锁详解
- Java并发包源码学习系列:ReentrantReadWriteLock读写锁解析
- Java并发包源码学习系列:详解Condition条件队列、signal和await
- Java并发包源码学习系列:挂起与唤醒线程LockSupport工具类
- Java并发包源码学习系列:JDK1.8的ConcurrentHashMap源码解析
- Java并发包源码学习系列:阻塞队列BlockingQueue及实现原理分析
- Java并发包源码学习系列:阻塞队列实现之ArrayBlockingQueue源码解析
- Java并发包源码学习系列:阻塞队列实现之LinkedBlockingQueue源码解析
PriorityBlockingQueue概述
PriorityBlockingQueue是一个支持优先级的无界阻塞队列,基于数组的二叉堆,其实就是线程安全的PriorityQueue。
指定排序规则有两种方式:
- 传入PriorityBlockingQueue中的元素实现Comparable接口,自定义
compareTo方法。 - 初始化PriorityBlockingQueue时,指定构造参数
Comparator,自定义compare方法来对元素进行排序。
需要注意的是如果两个对象的优先级相同,此队列并不保证它们之间的顺序。
PriorityBlocking可以传入一个初始容量,其实也就是底层数组的最小容量,之后会使用tryGrow扩容。
类图结构及重要字段
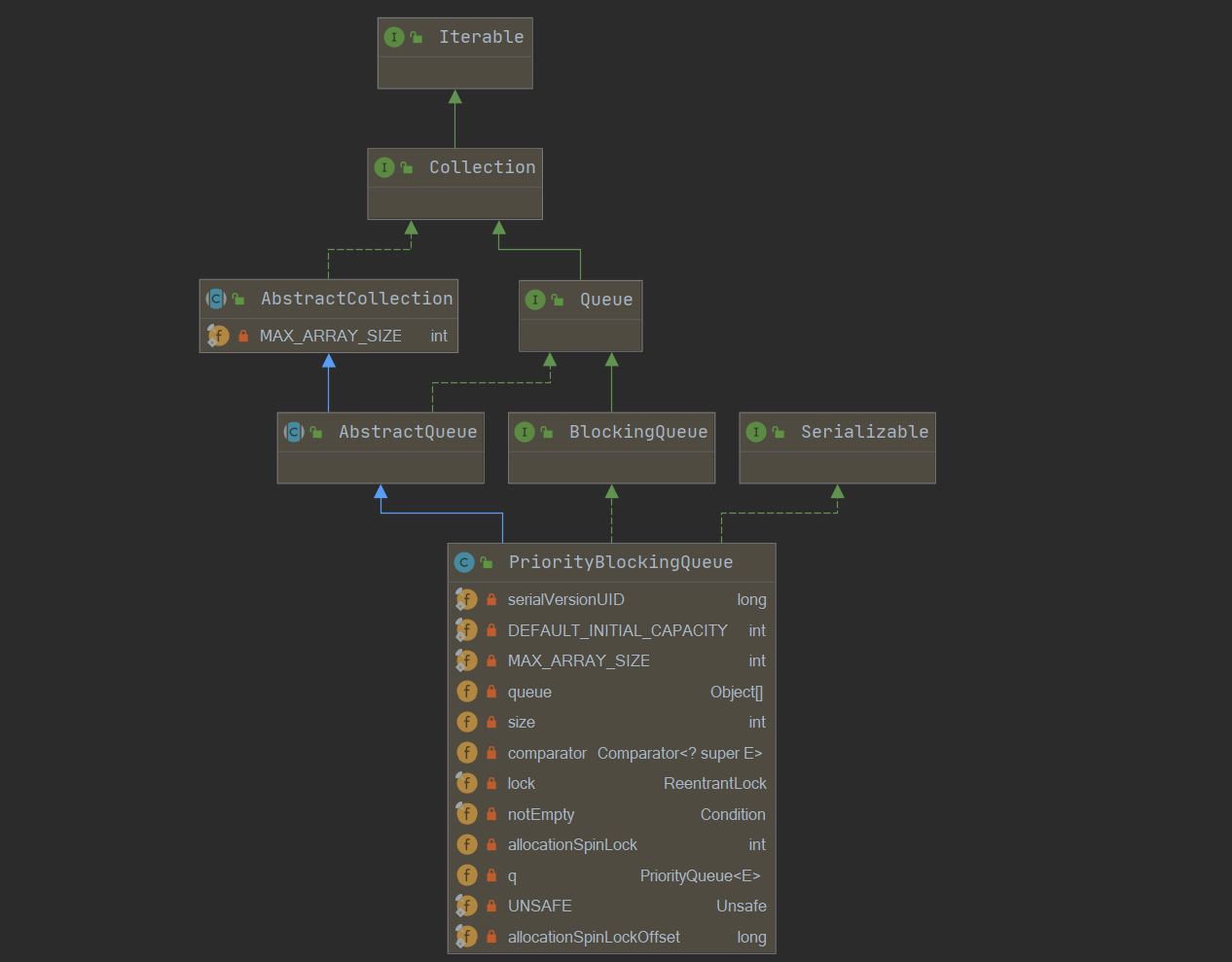
public class PriorityBlockingQueue<E> extends AbstractQueue<E>
implements BlockingQueue<E>, java.io.Serializable {
private static final long serialVersionUID = 5595510919245408276L;
/**
* 默认的容量为 11
*/
private static final int DEFAULT_INITIAL_CAPACITY = 11;
/**
* 数组的最大容量
*/
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
/**
* 平衡二叉堆 实现 优先级队列, 底层用数组结构存储二叉堆
* 假设一个n为数组中的索引,数组是从索引0开始存储元素的,因此
* queue[n]的左儿子存在queue[2*n+1]位置,右儿子存在queue[2*(n+1)]位置
*
* 根据比较器排序,如果没有指定比较器,则按照元素自然顺序排序。
* 默认是小根堆,第一个元素是堆中最小元素
*
*/
private transient Object[] queue;
/**
* 优先级队列中元素个数
*/
private transient int size;
/**
* 比较器,如果按照自然序排序,那么此属性可设置为 null
*/
private transient Comparator<? super E> comparator;
/**
* 所有需要保证线程安全的操作都要先获取这把锁
*/
private final ReentrantLock lock;
/**
* 队列空的时候,条件队列存放阻塞线程,为什么没有队列满呢?原因在于它是无界队列
*/
private final Condition notEmpty;
/**
* 用于CAS操作,后面会看到,这个字段用于扩容时
*/
private transient volatile int allocationSpinLock;
/**
* 只用于序列化和反序列化
*/
private PriorityQueue<E> q;
}
什么是二叉堆
这边安利一个数据结构的可视化网站:数据结构可视化网站
二叉堆是完全二叉树,除了最后一层,其他节点都是满的,且最后一层节点从左到右排列,如下:
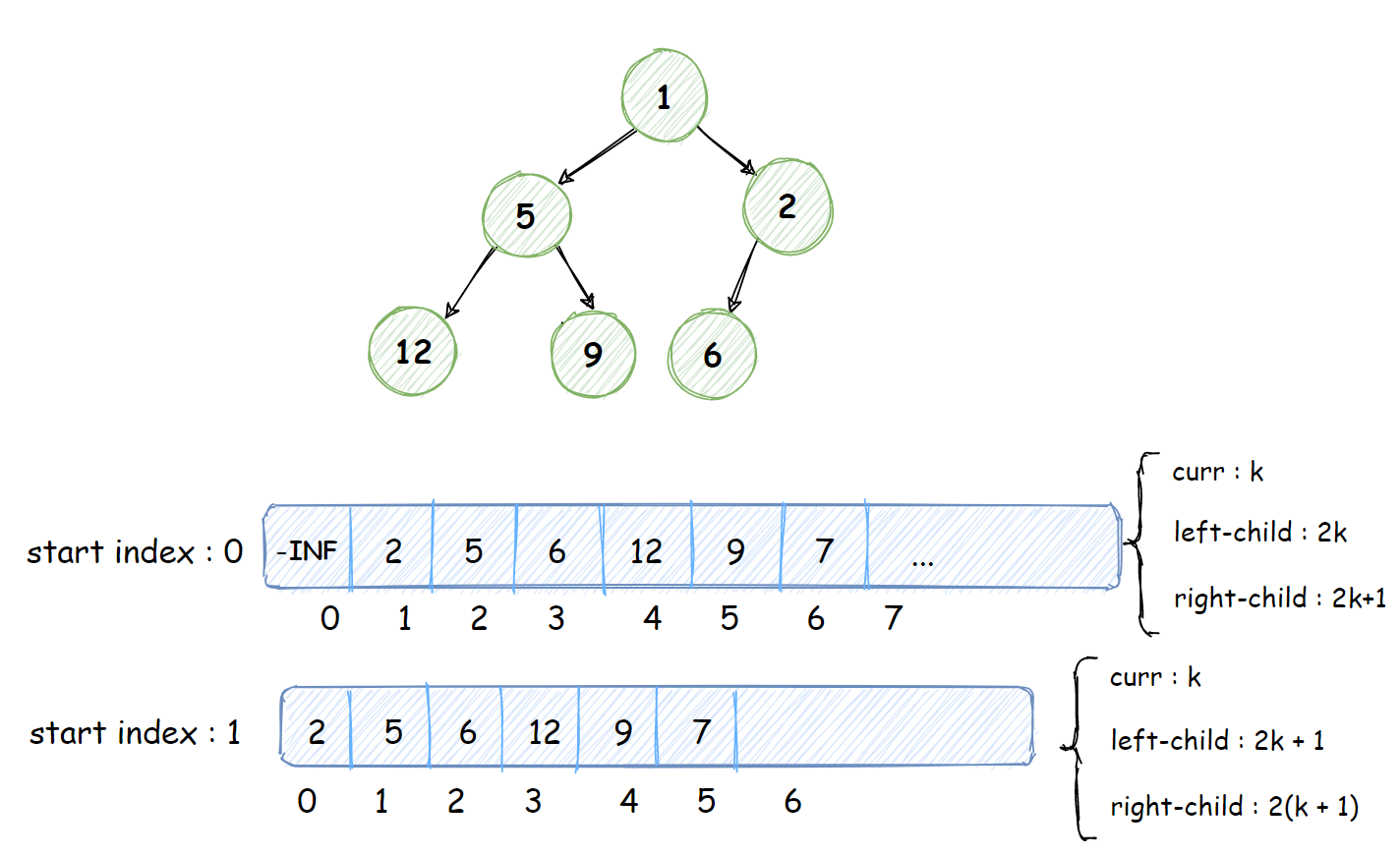
二叉堆分为大根堆和小根堆,一般来说都是小根堆,任意一个节点都小于它的左右子节点的值,根节点就是堆中的最小的值。
堆可以使用数组存储,数组的下标可以从0开始,也可以从1开始,各有好处,当然JDK中堆的实现是从0开始的哦。
- 如果从索引为1的位置开始存储元素,第k个节点的左右子节点的下标:(2k, 2k + 1),父节点的坐标可以很容易求:
floor(k / 2),floor表示下取整。 - 如果从0开始,第k个节点的左右子节点的下标:(2k + 1, 2k + 2),父节点的坐标也可以很容易求:
floor((k - 1) / 2),floor表示下取整。
我之前手写堆的时候,都是使用的第一种方式,我就提一嘴第一种的思路,使用第一种思路介绍一下小根堆的几个基本操作,之后我们会详细分析JDK中的实现,也就是第二种。
堆的基本操作
堆中最重要核心的两个操作便是如何将元素向上调整or向下调整。
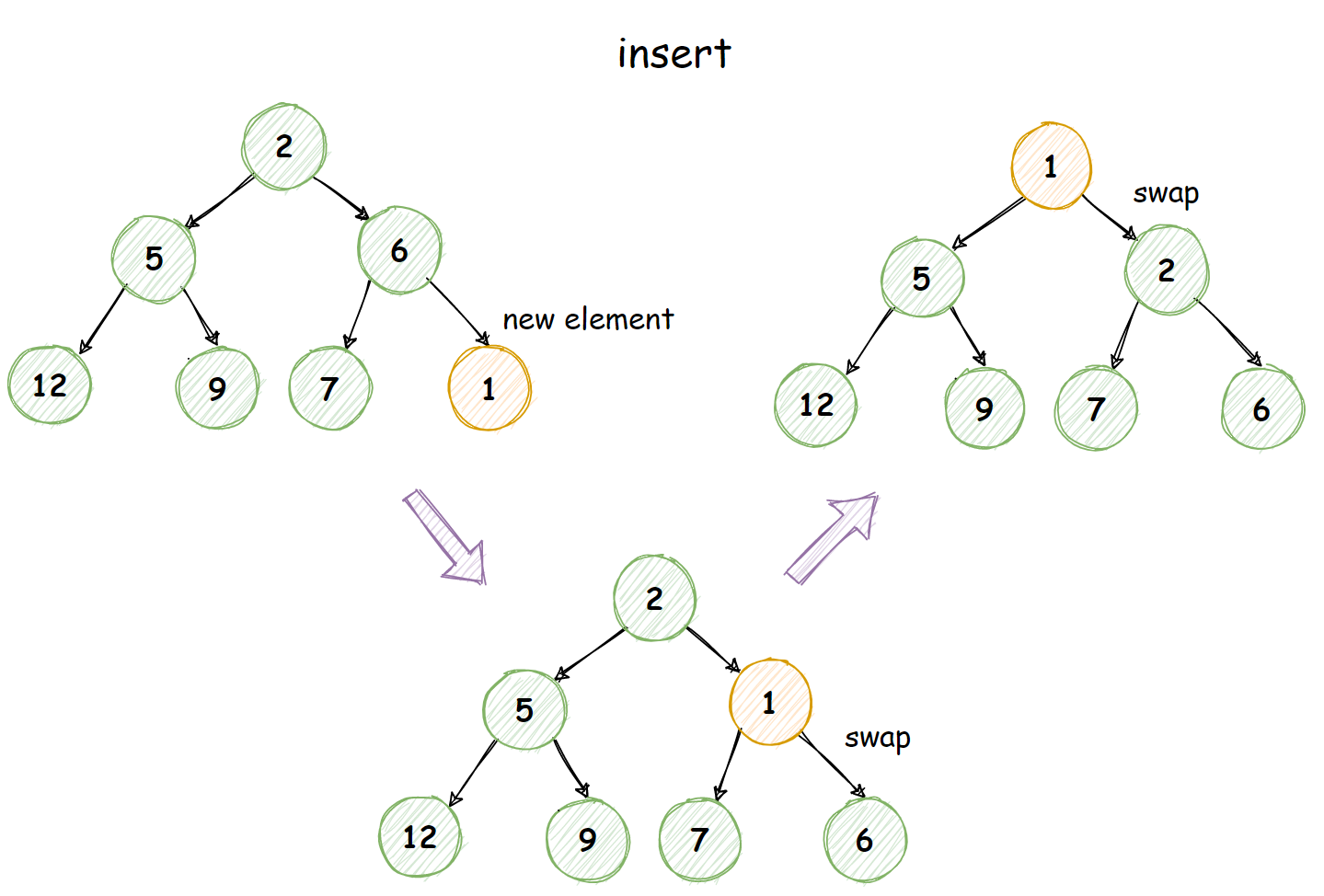
向上调整void up(int u)
以插入操作为例,二话不说,直接在数组末尾插上元素,接着再一一向上层比较,比较的原则的就是:我们只需要比较当前这个数是不是比它的父节点小,如果比它小,就进行交换,否则则停止交换。
思路非常简单,你可以思考一下其合理性:我们想,如果我们每次插入数据的时候,都做一次向上调整的操作,我们一定能够保证,每次都是在一个符合条件的二叉堆上插入数,对吧。那这样的话,本身就满足任何一个父节点必定比其子节点小的条件,如果待调整节点更小,那他必然也小于另一个子节点,由于我们一直迭代做,最后一定会满足条件。
// 向上调整 u 是当前的索引
private void up (int u) {
// 如果发现当前的节点比父节点小
while (u / 2 > 0 && h[u / 2] > h[u]) {
// 就和父节点交换一下
heap_swap(u / 2, u);
u /= 2;
}
}
这边也给出插入一个元素x的伪代码:
void insert(int x){
size ++; // 最后一个元素指针
heap[size] = x; // 赋值
up(size); // 向上调整
}
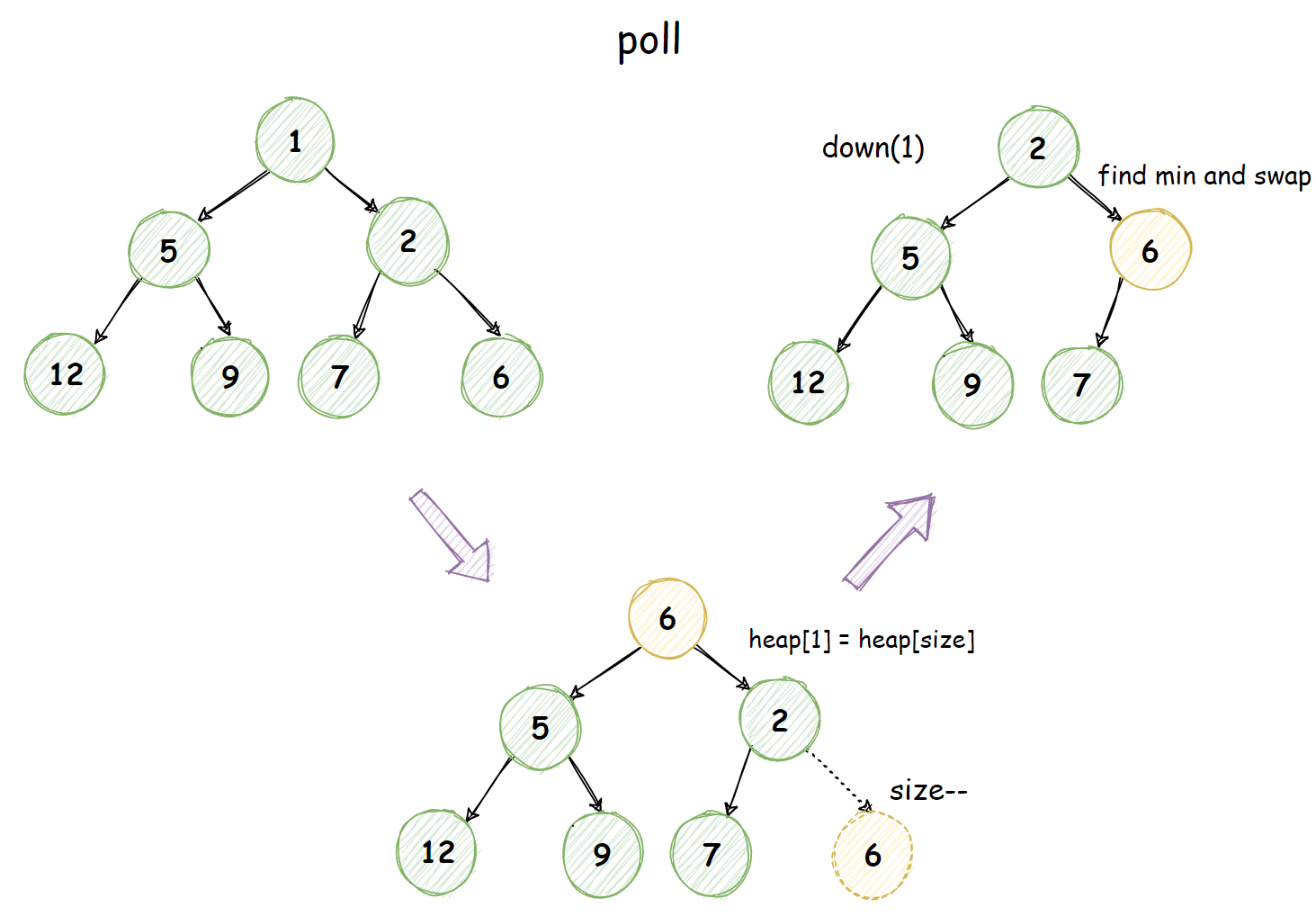
向下调整void down(int u)
为什么需要向下调整呢,以删除操作为例,我们知道,要在数组头部删除一个元素且保证后面元素的顺序是比较麻烦的,我们通常在遇到删除堆顶的时候,直接将数组的最后一个元素heap[size--]将heap[0]覆盖,接着执行down(0),自上而下地执行调整操作。
调整的规则也比较简单,其实就是判断当前元素和左右孩子的大小关系,和最小的那个交换,递归地去调整,直到无法交换为止。
// 向下调整
private void down (int u) {
int t = u;
if (u * 2 <= size && h[u * 2] < h[t]) t = u * 2; // 判断左儿子是否存在, 且如果左儿子比它小,就更新坐标
if (u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) t = u * 2 + 1; // 同理
if (u != t) { // 如果需要交换
heap_swap(u, t);// 交换一下
down(t); // 继续做这个操作
}
}
这边给出删除小根堆中的最小值的伪代码:
int poll(){
int res = heap[1]; // 堆顶是最小值
heap[1] = heap[size--]; // 直接将最后一个元素覆盖堆顶,并size-1
down(1); // 执行向下调整
return res;
}
我们希望删除第k个元素或者更新第k个元素都是比较简便的:
// 删除位置为k的元素
void removeAt(int k){
heap[k] = heap[size --];
// 分别做一次向下操作和向上操作,其中一个判断必定只会执行一次
down(k);
up(k);
}
// 更新位置为k的元素为x
void updateAt(int k, int x){
heap[k] = x;
down(k);
up(k);
}
到这里,我就用简略代码简单地介绍了二叉堆的核心操作,我们待会会看到其实源码的思想不变,但是考虑的东西会更多一些,如果到这里你能够完全明白,源码的实现其实也就不难啦。
构造器
// 使用默认的容量11
public PriorityBlockingQueue() {
this(DEFAULT_INITIAL_CAPACITY, null);
}
// 指定容量大小
public PriorityBlockingQueue(int initialCapacity) {
this(initialCapacity, null);
}
// 指定容量和比较器
public PriorityBlockingQueue(int initialCapacity,
Comparator<? super E> comparator) {
if (initialCapacity < 1)
throw new IllegalArgumentException();
this.lock = new ReentrantLock();
this.notEmpty = lock.newCondition();
this.comparator = comparator;
this.queue = new Object[initialCapacity];
}
// 传入集合
public PriorityBlockingQueue(Collection<? extends E> c) {
this.lock = new ReentrantLock();
this.notEmpty = lock.newCondition();
boolean heapify = true; // true if not known to be in heap order
boolean screen = true; // true if must screen for nulls
if (c instanceof SortedSet<?>) {
SortedSet<? extends E> ss = (SortedSet<? extends E>) c;
this.comparator = (Comparator<? super E>) ss.comparator();
heapify = false;
}
else if (c instanceof PriorityBlockingQueue<?>) {
PriorityBlockingQueue<? extends E> pq =
(PriorityBlockingQueue<? extends E>) c;
this.comparator = (Comparator<? super E>) pq.comparator();
screen = false;
if (pq.getClass() == PriorityBlockingQueue.class) // exact match
heapify = false;
}
Object[] a = c.toArray();
int n = a.length;
// If c.toArray incorrectly doesn't return Object[], copy it.
if (a.getClass() != Object[].class)
a = Arrays.copyOf(a, n, Object[].class);
if (screen && (n == 1 || this.comparator != null)) {
for (int i = 0; i < n; ++i)
if (a[i] == null)
throw new NullPointerException();
}
this.queue = a;
this.size = n;
// 需要堆化,后面说明该方法
if (heapify)
heapify();
}
接下来我将会把一些核心组件方法都拎出来分析一下,他们很有可能会在后面的操作方法中被频繁调用,所以接下来很重要哦。
扩容方法tryGrow
我们说了,PriorityBlockingQueue是无界的队列,传入的capacity也不是最终的容量,它和我们之前学习的许多集合一样,有动态扩容的机制,我们先来瞅一瞅:
private void tryGrow(Object[] array, int oldCap) {
// 释放锁的操作
lock.unlock(); // must release and then re-acquire main lock
Object[] newArray = null;
// CAS 操作将allocationSpinLock变为1, 如果已经是1了,就跳到下面
if (allocationSpinLock == 0 &&
UNSAFE.compareAndSwapInt(this, allocationSpinLockOffset,
0, 1)) {
try {
// 节点个数<64 new = old + old + 2
// 节点个数>=64 new = old + old / 2
int newCap = oldCap + ((oldCap < 64) ?
(oldCap + 2) : // 希望节点数较小的时候,增长快一点
(oldCap >> 1));
// 扩容之后越界了
if (newCap - MAX_ARRAY_SIZE > 0) { // possible overflow
int minCap = oldCap + 1;
if (minCap < 0 || minCap > MAX_ARRAY_SIZE)
throw new OutOfMemoryError();
newCap = MAX_ARRAY_SIZE;
}
//queue != array 的情况 其他线程已经为queue分配了其他的空间
if (newCap > oldCap && queue == array)
// 分配一个加大容量的数组
newArray = new Object[newCap];
} finally {
allocationSpinLock = 0;
}
}
// 可能是其他线程在进行扩容操作
if (newArray == null) // back off if another thread is allocating
Thread.yield();
// 重新获取锁
lock.lock();
// 复制元素
if (newArray != null && queue == array) {
queue = newArray;
System.arraycopy(array, 0, newArray, 0, oldCap);
}
}
可以发现的是,在动态扩容之前,将lock释放,表明这个方法一定是在获取锁之后才被调用的。
为啥在扩容之前先释放锁,并使用CAS控制只有一个线程可以扩容成功呢?
扩容是需要时间的,如果在整个扩容期间一直持有锁的话,其他线程在这时是不能进行出队和入队操作的,这大大降低了并发性能。
spinlock锁使用CAS控制只有一个线程可以进行扩容,失败的线程执行
Thread.yield()让出CPU,目的是让扩容的线程优先调用lock.lock()优先获取锁,但是这得不到保证,因此需要后面的判断。另外自旋锁变量allocationSpinLock在扩容结束后重置为0,并没有使用UNSAFE方法的CAS进行设置是因为:
- 同时只可能有一个线程获取到该锁。
- allocationSpinLock是volatile修饰。
源码中向上调整和向下调整实现
准确地说,源码中应该是调整 + 插入,不断调整,找到插入的位置,给该位置赋值。但,如果你理解了前面的调整思想,相信你会很快理解源码中的实现。
siftUpComparable
将x插入到堆中,注意这里是不断和父节点比较,最终找到插入位置。
// 将x插入到堆中,注意这里是不断和父节点比较,最终找到插入位置
private static <T> void siftUpComparable(int k, T x, Object[] array) {
// 如果不传入Comparable的实现,这里会强转失败,抛出异常
Comparable<? super T> key = (Comparable<? super T>) x;
while (k > 0) {
//a[k]的父节点位置
int parent = (k - 1) >>> 1;
Object e = array[parent];
// 如果比父节点大就不用交换了
if (key.compareTo((T) e) >= 0)
break;
// 将父元素移下来
array[k] = e;
// k向上移
k = parent;
}
// 退出循环后,k的位置就是待插入的位置
array[k] = key;
}
siftDownComparable
移除k位置的元素,并调整二叉堆,具体思想就是,一般通过向下调整找到覆盖位置,用x覆盖即可,x一般可以从队尾获取。
// 这里的k就是当前空缺的位置,x就是覆盖元素比如我们之前说的队尾元素
private static <T> void siftDownComparable(int k, T x, Object[] array,
int n) {
if (n > 0) {
Comparable<? super T> key = (Comparable<? super T>)x;
// 二叉堆有一个性质,最后一层叶子最多 占 1 / 2
int half = n >>> 1; // loop while a non-leaf
// 循环非叶子节点
while (k < half) {
// 左孩子
int child = (k << 1) + 1; // assume left child is least
Object c = array[child];
// 右孩子
int right = child + 1;
// 始终用左孩子c表示最小的数
if (right < n &&
((Comparable<? super T>) c).compareTo((T) array[right]) > 0)
// 这里如果右孩子小,更新child = right
c = array[child = right];
// 如果当前的k比左孩子还要小,那就不必交换了,待在那正好!
if (key.compareTo((T) c) <= 0)
break;
// 小的数向上移,k向下更新
array[k] = c;
k = child;
}
// 退出循环时,一定找到了x覆盖的位置,覆盖即可
array[k] = key;
}
}
你看看,理解了调整的思想之后,看起代码来是不是就相对轻松很多啦?
heapify建堆or堆化
heapify方法可以使节点任意放置的二叉树,在O(N)的时间复杂度内转变为二叉堆,具体做法是,从最后一层非叶子节点自底向上执行down操作。
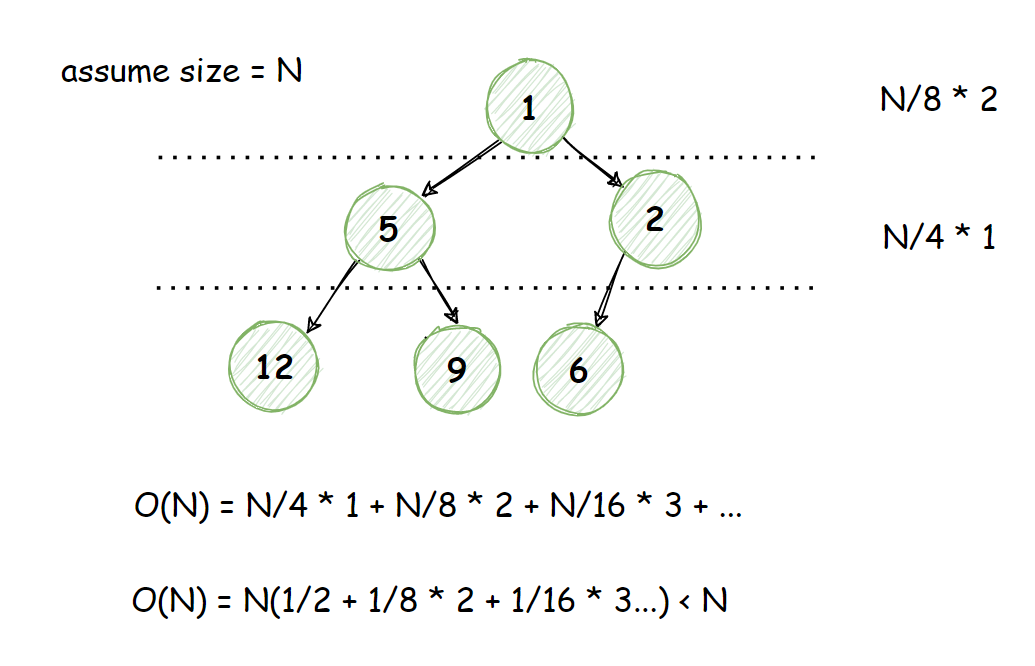
private void heapify() {
Object[] array = queue;
int n = size;
int half = (n >>> 1) - 1; // 最后一层非叶子层
// 两种排序规则下, 自底向上 地执行 siftdown操作
Comparator<? super E> cmp = comparator;
if (cmp == null) {
for (int i = half; i >= 0; i--)
siftDownComparable(i, (E) array[i], array, n);
}
else {
for (int i = half; i >= 0; i--)
siftDownUsingComparator(i, (E) array[i], array, n, cmp);
}
}
put非阻塞式插入
put方法是非阻塞的,但是操作时需要获取独占锁,如果插入元素后超过了当前的容量,会调用tryGrow进行动态扩容,接着从插入元素位置进行向上调整,插入成功后,唤醒正在阻塞的读线程。
public void put(E e) {
offer(e); // 无界队列,插入操作不需要阻塞哦
}
public boolean offer(E e) {
if (e == null)
throw new NullPointerException();
final ReentrantLock lock = this.lock;
lock.lock();
int n, cap;
Object[] array;
// 当前队列中的元素个数 >= 数组的容量
while ((n = size) >= (cap = (array = queue).length))
// 动态扩容
tryGrow(array, cap);
try {
Comparator<? super E> cmp = comparator;
// 下面这个if else根据是否传入比较器选择对应的方法,大差不差
if (cmp == null)
siftUpComparable(n, e, array);
else
siftUpUsingComparator(n, e, array, cmp);
size = n + 1;
// 唤醒正在阻塞的读线程
notEmpty.signal();
} finally {
lock.unlock();
}
return true;
}
take阻塞式获取
take方法是阻塞式的,如果队列为空,则当前线程阻塞在notEmpty维护的条件队列中。
public E take() throws InterruptedException {
final ReentrantLock lock = this.lock;
// 获取锁
lock.lockInterruptibly();
E result;
try {
// 出队
while ( (result = dequeue()) == null)
notEmpty.await();
} finally {
lock.unlock();
}
return result;
}
// 出队逻辑
private E dequeue() {
int n = size - 1;
if (n < 0)
return null;
else {
Object[] array = queue;
// 保存队头的值,也就是返回这个值
E result = (E) array[0];
// 准备将队尾的值 覆盖第一个
E x = (E) array[n];
array[n] = null;
Comparator<? super E> cmp = comparator;
if (cmp == null)
siftDownComparable(0, x, array, n);
else
siftDownUsingComparator(0, x, array, n, cmp);
size = n;
return result;
}
}
remove移除指定元素
public boolean remove(Object o) {
final ReentrantLock lock = this.lock;
lock.lock();
try {
// 找到匹配元素下标
int i = indexOf(o);
if (i == -1)
return false;
// 移除该下标的元素
removeAt(i);
return true;
} finally {
lock.unlock();
}
}
// 遍历底层数组, 找到匹配元素的下标
private int indexOf(Object o) {
if (o != null) {
Object[] array = queue;
int n = size;
for (int i = 0; i < n; i++)
if (o.equals(array[i]))
return i;
}
return -1;
}
// 移除下标为i的元素
private void removeAt(int i) {
Object[] array = queue;
int n = size - 1;
if (n == i) // removed last element
array[i] = null;
else {
// 老套路了,让队尾的元素覆盖这里
E moved = (E) array[n];
array[n] = null;
Comparator<? super E> cmp = comparator;
// 向下调整
if (cmp == null)
siftDownComparable(i, moved, array, n);
else
siftDownUsingComparator(i, moved, array, n, cmp);
// 向下调整没成功,向上调整
if (array[i] == moved) {
if (cmp == null)
siftUpComparable(i, moved, array);
else
siftUpUsingComparator(i, moved, array, cmp);
}
// 这也是惯用做法,上下分别做一次调整
}
size = n;
}
总结
PriorityBlockingQueue是一个支持优先级的无界阻塞队列,基于数组的二叉堆,其实就是线程安全的PriorityQueue。
内部使用一个独占锁来同时控制只有一个线程执行入队和出队操作,只是用notEmpty条件变量来控制读线程的阻塞,因为无界队列中入队操作是不会阻塞的。
指定排序规则有两种方式:
- 传入PriorityBlockingQueue中的元素实现Comparable接口,自定义
compareTo方法。 - 初始化PriorityBlockingQueue时,指定构造参数
Comparator,自定义compare方法来对元素进行排序。
底层数组是可动态扩容的:先释放锁,保证扩容操作和读操作可以同时进行,提高吞吐量,接着通过CAS自旋保证扩容操作的并发安全,如果原容量为old_c,扩容后容量为new_c,满足:
if (old_c < 64)
new_c = 2 * old_c + 2
else
new_c = 1.5 * old_c
heapify方法可以使节点任意放置的二叉树,在O(N)的时间复杂度内转变为二叉堆,具体做法是,从最后一层非叶子节点自底向上执行down操作。
参考阅读
-
《Java并发编程的艺术》
-
《Java并发编程之美》


