如果矩阵A满足以下性质,我们称其为分形排序矩阵:
(1)矩阵A中的元素从小到大或从大到小都是不规则的;
(2)矩阵A中的元素的顺序是自相似的;
(3)矩阵A可以通过迭代生成,并且可以通过无限迭代生成无限矩阵。
分形:通常被定义为"一个粗糙或零碎的几何形状,可以分成数个部分,且每一部分都(至少近似地)是整体缩小后的形状",即具有自相似的性质。
分形实例:

我们可以看到罗马花椰菜一小簇是整个花簇的一个分支,而在不同尺度下它们具有自相似的外形。换句话说,较小的分支通过放大适当的比例后可以得到一个与整体几乎完全一致的花簇。
自相似性,如果一个物体自我相似,表示它和它本身的一部分完全或是几乎相似。
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
假设我们有个2×2的矩阵A1=[4,2;1,3],通过一次迭代,生成4×4的矩阵A2,如下图:
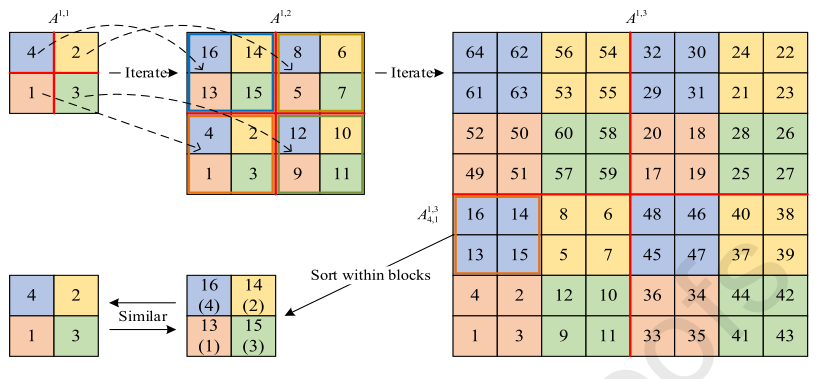
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | clear all;close all;E=cell(1,5); % 生成一个1×5阶的置空的单元数组A1=[4 2;1 3]; % 初始化A1E{1}=A1;tic % 用来保存当前时间for k=2:5 % 通过迭代生成Ak q=k-1; % 上一次迭代的矩阵的阶数 mn=size(E{q}); % 上一次迭代的矩阵的维数 % ones(size(A)) 创建与A维数相同的全1阵 % 2^3表示2的3次方 B1=(A1(1,1)-1)*(2^(2*(k-1)))*ones(mn)+E{q}; B2=(A1(1,2)-1)*(2^(2*(k-1)))*ones(mn)+E{q}; B3=(A1(2,1)-1)*(2^(2*(k-1)))*ones(mn)+E{q}; B4=(A1(2,2)-1)*(2^(2*(k-1)))*ones(mn)+E{q}; E{k}=[B1,B2;B3,B4];endtoc % 记录程序完成时间 |
执行结果如下:
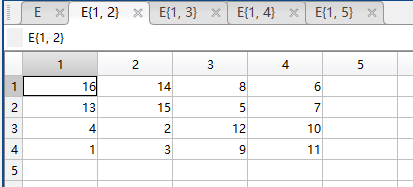
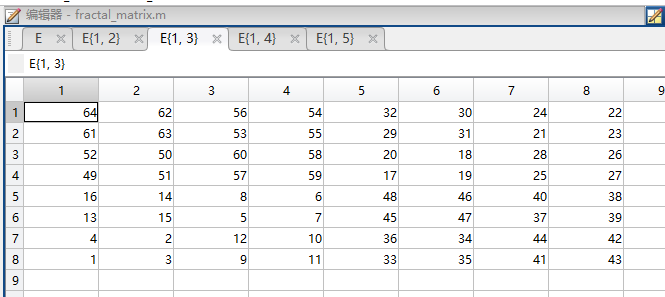




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:基于图像分类模型对图像进行分类
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 25岁的心里话
· 闲置电脑爆改个人服务器(超详细) #公网映射 #Vmware虚拟网络编辑器
· 零经验选手,Compose 一天开发一款小游戏!
· 因为Apifox不支持离线,我果断选择了Apipost!
· 通过 API 将Deepseek响应流式内容输出到前端