python 算法 day11 图 词梯
图
顶点 vertex:是图的基础部分
边 edge:如果一个边连接两个点,则表示两者具有联系,边可以是单向的也可以是双向的,如果一个图中的边都是单向的,我们就说这个图是有向图
权重 weight:一个顶点到另一个顶点的“代价”,可以给边赋权
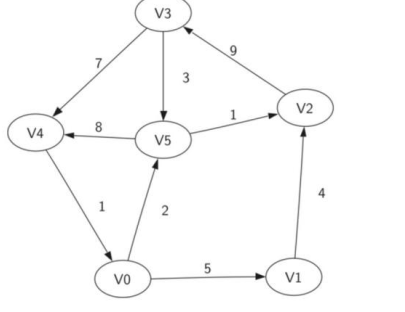
路径 path:由边依次连接起来的顶点序列
圈 cycle:有向图里的圈是首尾顶点相同的路径
邻接矩阵
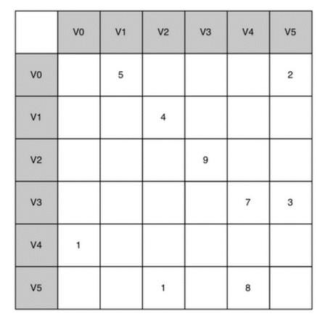
用邻接矩阵表示图的优点是简单,很容易看出节点之间的联系状态,然而会有大量的矩阵分量是空的
邻接表
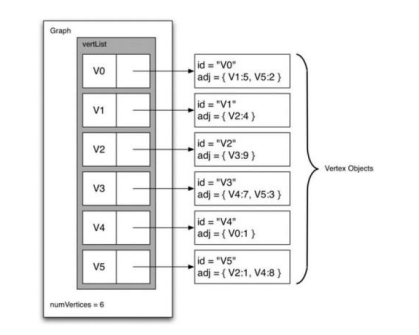
一个更高效的方法是使用邻接表,我们采用维护一个包含所有顶点的主列表,再关联一个与自身有边连接的所以顶点的列表,我们采用字典来实现顶点类,字典中的key对应连接的顶点标示,value对应与自身连接的点的权重
class Vertex: def __init__(self,key): self.id = key self.connectedTo = {} def addNeighbor(self,nbr,weight=0): self.connectedTo[nbr] = weight #添加邻居节点以及权重 def __str__(self): return str(self.id) + 'connectedTo:'+str([x.id for x in self.connectedTo]) def getConnections(self): return self.connectedTo.keys() #返回所有连接的邻居节点 def getId(self): return self.id def getWeight(self,nbr): return self.connectedTo[nbr]
图的类是把刚才的顶点类和顶点重新构造成一个字典
class Graph: def __init__(self): self.vertList = {} self.numVertices = 0 def addVertex(self,key): self.numVertices = self.numVertices + 1 newVertex = Vertex(key) self.vertList[key] = newVertex 将顶点作为一个对象储存在字典中 每一个顶点标示和对应的对象存放在字典中 return newVertex def getVertex(self,n): if n in self.vertList: return self.vertList[n] else: return None def __contains__(self, item): 重载in return item in self.vertList def addEdge(self,f,t,cost=0): if f not in self.vertList: nv = self.addVertex(f) 增加边 首先判断两个节点是否在图中 if t not in self.vertList: nv = self.addVertex(t) self.vertList[f].addNeighbor(self.vertList[t],cost) def getVertices(self): return self.vertList.keys() def __iter__(self): return iter(self.vertList.values())
词梯问题
- 以图的形式描绘出单词间的关系
- 利用广度优先搜索(BFS)的图算法找到一条从开始单词到目标单词的最短路径
首先解决如何将大量单词组成的集合转变成图,我们先假设我们有一个单词列表,其中的单词都一样长,我们可以为列表里的每个单词在图中创建一个顶点,而为将这些单词连接起来,我们可以将列表中的每个词与所有其他单词比较,当我们比较的时候,我们要看到单词中有多少字母是不同的,如果两个词中只有一个字母不同,我们就可以在图中创建一条连接他们的边 算法复杂度是O(n2)
优化方法:假设我们有非常多的桶,每个桶外都贴有一个四字字母的单词标签,并且标签上有且只有一个字母被通配符-代替
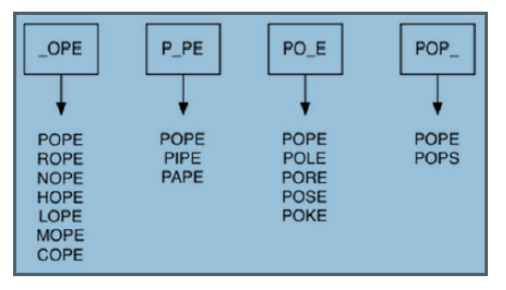
我们可以通过一个字典来实现 桶上的标签作为一个key值 value对应桶里单词的列表
from pythonds.graphs import Graph def buildGraph(wordFile): d = {} g = Graph() w_file = open(wordFile,'r') 这里文件每行只有一个单词 for line in w_file: word = line[:-1] 去除行结尾的回车字符 for i in range(len(word)): bucket = word[:i]+'_'+word[i+1:] 将第i个字符去除作为通配符 if bucket in d: d[bucket].append(word) else: d[bucket] = [word] for bucket in d.keys(): for word1 in d[bucket]: for word2 in d[bucket]: if word1 !=word2: g.addEdge(word1,word2)
实现广度优先搜索(BFS)
已知一个图G和它的一个起始节点s,广度优先搜索(BFS)通过搜索图中的边来找到图G中所有和s有路径相连的顶点,其显著特点是在搜索达到距离k+1的顶点之前,BFS会找全部距离为k的顶点 为了追踪这一过程,会给每一个搜索过的顶点染成灰色 每一个顶点在被构建时都初始化为白色,当完全搜索完一个层级的节点时 它会被染成黑色,这意味着一旦一个节点染成黑色,它就没有邻近的白色节点,而另一方面,如果一个顶点被标示成了灰色,这就意味这附近还可能存在为探索的顶点等待被探索
节点类中还需添加三个新的实例变量:距离 父顶点和颜色
对于起始节点 设置0和None 随后起始节点加入一个队列中,下一步便是系统地搜索队首顶点,这个过程通过迭代遍历队首顶点的邻接列表来完成,每检查邻接表中的一个顶点,便会维护这个顶点的颜色变量:
- 新的未探索的顶点nbr 标记成灰色
- nbr的父顶点被设置成当前节点currentVert
- nbr的距离被设置成当前节点的距离+1
- nbr被加入队尾,这一操作使得直到nbr在当前顶点的邻接列表中所有节点被搜索完后,才能进行下一层次的探索操作
def bfs(g,start): start.setDistance(0) start.setPred = None vertQueue = Queue() vertQueue.enqueue(start) while (vertQueue.size()>0): 直到队列中没有元素 currentVert = vertQueue.dequeue() for nbr in currentVert.getConnections(): if(nbr.getColor()=='white'): nbr.setColor('gray') nbr.setDistance(currentVert.getDistance()+1) nbr.setPred(currentVert) vertQueue.enqueue(nbr) 每次标记完节点 再把下一层节点 为白色的加入队列 直到最后没有元素
对BFS的分析:
当while循环被执行时,图的顶点集合|v|的每个顶点最多被访问一次,因而while循环拥有O(V)的复杂度 while中的for循环语句,对于图的边集|E|中的每一条边至多会被执行一次,这是因为每个顶点只会最多被出队一次,对于从顶点u到顶点v的边,只有当顶点u出队的时候我们才会检查,所以每条边最多被检查一次 算法复杂度为O(V+E)



