python 算法 day9 二叉堆
为了使堆操作高效运行,我们将利用二叉树的操作复杂度为对数级这一性质来实现堆操作。同时使堆操作的复杂度始终保持在对数水平上,就必须保持二叉树的平衡,平衡二叉树树根左右子树有着相同的数量节点。完全二叉树,指每个内部节点都有两个子节点,最多可有一个节点列外。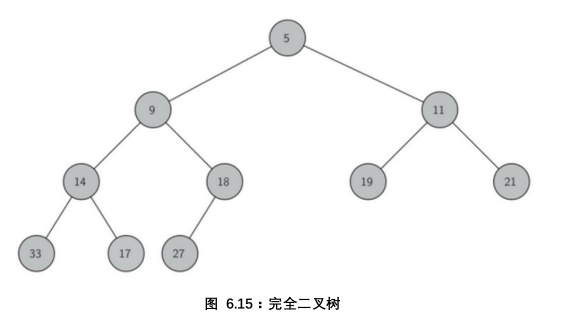
完全树的另一个特性,我们可以用单个列表来实现完全树而不需要使用节点,如果节点在列表中的位置为p,那么其左子节点的位置为2p 右子节点位置为2p+1
堆次序:
指堆中任意一个节点x,其父节点p中的key均小于或等于x中的key 兄弟节点没有要求

实现一个二叉堆:可以采用一个列表来保存堆数据,构造函数初始化仅仅需要初始化一个列表和一个currentSize来跟踪记录当前堆的大小
class BinHeap: def __init__(self): self.heapList = [0] self.currentSize = 0 def percUp(self,i): #使新节点上浮到正确位置 while i//2 > 0: if self.heapList[i] < self.heapList[i//2]: tmp = self.heapList[i//2] self.heapList[i//2] = self.heapList[i] self.heapList[i] = tmp i = i//2 def insert(self, k): self.heapList.append(k) self.currentSize = self.currentSize + 1 self.percUp(self.currentSize) def percDowm(self,i): #替换节点下沉 while (i * 2)<= self.currentSize: mc = self.minChild(i) if self.heapList[i]>self.heapList[mc]: tmp = self.heapList[i] self.heapList[i] = self.heapList[mc] self.heapList[mc] = tmp i = mc def minChild(self,i): if i*2+1 >self.currentSize: return i*2 else: if self.heapList[i*2] < self.heapList[i*2+1]: return i*2 else: return i*2+1 def delMin(self): #比较容易移走最小项 但移走根节点数据后如何恢复堆结构和堆次序比较困难
retval = self.heapList[1]
self.heapList[1] = self.heapList[self.currentSize]
self.heapList.pop()
self.currentSize = self.currentSize -1
self.percDowm(1)
return retval
def buildHeap(self,alist):
i = len(alist)//2
self.currentSize =len(alist)
self.heapList = [0] +alist[:]
while(i>0):
self.percDowm(i)
i = i -1
.如何恢复堆结构和堆次序:首先用最后一个节点来代替根节点,移走最后一个节点维持了堆结构的性质,简单替换 但很可能破坏堆次序
第二步 用新替换的节点来下沉恢复堆次序二叉堆的最后一个方法buildHeap是从无序表中生成一个堆,如果采用insert方法,复杂度是onlogn,多次调用insert是把数据一个个放进来,而buildheap是把整个列表中的所有元素全部放进来,再挑几个下沉在on复杂度下生成二叉堆,因为二叉堆只保证父子间的顺序,并不保证兄弟间的大小。
二叉搜索树
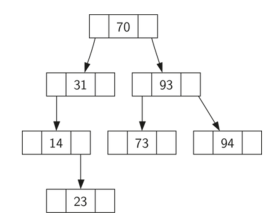
一个二叉搜索树,如果左子树的键值Key都小于父节点,而右子树中键值Key都大于父节点,我们将这种树称为BST搜索树
所有左子树的键值都小于右子树的键值
实现二叉搜索树,使用节点和引用方法
用put方法创建二叉搜索树BST,先检查树是否已经有根节点,如果没有,put将根据传入的参数创建一个新的TreeNode并把它作为树的根节点,作为子树的根,如果一个根节点已经到位,我们就调用它自己进行递归 用_put方法来搜索树:
首先,从树的根开始搜索,比较新的键值,如果新的键值小于当前根的值,搜索左子树,如果大于,就搜索右子树
当无左子树或右子树时,我们发现的位置就是安装新节点的位置
向树添加一个新的节点,在上一步发现插入对象的位置创建一个新的TreeNode。
def put(self,key,val): if self.root: self._put(key,val,self.root) else: self.root = TreeNode(key,val) self.size = self.size+1 def _put(self,key,val,currentNode): if key<currentNode.key: if currentNode.hasleftChild(): self._put(key,val,currentNode.leftChild) 遍历递归到最下方没有子节点的位置 else: currentNode.leftChild = TreeNode(key,val,parent=currentNode) else: if currentNode.hasrightChild(): self._put(key,val,currentNode.rightChild) else: currentNode.rightChild = TreeNode(key,val,parent=currentNode)
树被构建后,接下来就是给定键实现对值的检索,get采用递归的搜索子树,直到发现匹配的值就返回
def get(self,key): if self.root: res = self._get(key,self.root) if res: return res.payload else: return None else: return None def _get(self,key,currentNode): if not currentNode: return None elif currentNode.key ==key: return currentNode elif key <currentNode.key: return self._get(key,currentNode.leftChild) else: return self._get(key,currentNode.rightChild)
一些小TIPs
__contains__()方法 从而能够实用操作符 in
__setitem__()方法 重载[]为操作符
__getitem__()方法 可以使我们像访问字典一样调用
def __getitem__(self, item): return self.get(item) def __contains__(self, key): if self._get(key,self.root): return True else: return False def __setitem__(self, key, value): self.put(key,value)
删除方法:我们可以使用get方法去找到需要删除的树节点,一旦找到我们需要删除的键的节点,有三种情况:
1、要删除的节点没有子树 只需要父节点对此节点的引用指向None
2、要删除的节点只有一个子节点
如果当前节点有左子节点,我们只需要更新当前节点的左子节点指向当前节点的父节点引用,然后将父节点对当前节点的引用更新到当前节点的左子节点
如果当前节点有右子节点,我们只需要更新当前节点的右子节点指向当前节点的父节点引用,然后将父节点对当前节点的引用更新到当前节点的右子节点
如果当前节点为根节点(没有父节点)则只需更换键
3、要删除的节点有两个子节点
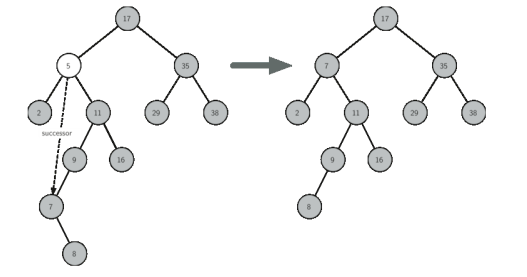
如果有两个子节点,我们不能简单的选其中一个提升至父节点的位置,这就需要寻找一个节点,用来替代一个计划删除的节点,还需要保持现有的 左右子树以及二叉搜索树的关系
符合该要求的是比要删节点大的第一个值 即在右子树上寻找最左子树 比如上图比5大的第一个值是7,我们通过寻找该节点,保证其没有一个以上的子节点,然后将其移动到删除节点处 并保证保证原有子树的位置
def spliceOut(self): if self.isLeaf(): if self.isLeftChild(): self.parent.leftChild = None else: self.parent.rightChild = None elif self.hasAnyChildren(): if self.hasLeftChild(): if self.isLeftChild(): self.parent.leftChild = self.leftChild else: self.parent.rightChild = self.leftChild self.leftChild.parent = self.parent else: self.parent.rightChild = self.leftChild self.leftChild.parent = self.parent else: if self.isLeftChild(): self.parent.leftChild = self.rightChild else: self.parent.rightChild = self.rightChild self.rightChild.parent = self.parent def findSuccessor(self): succ = None if self.hasRightChild(): succ = self.rightChild.findMin() else: if self.parent: if self.isLeftChild(): succ = self.parent else: self.parent.rightChild = None succ = self.parent.findSuccessor() self.parent.rightChild = self return succ def findMin(self): current = self while current.hasleftChild(): current = current.leftChild return current
找到继任者的函数findSuccessor() 需要考虑三种情况:
1、如果节点有右子节点,那么继任者是右子树中最小的键
2、如果节点没有右子节点,是其父节点的左子节点 ,则父节点是继任者
3、如果节点是其父节点的右子节点,而本身无右子节点,那么该节点的继任者是其父结点的继任者 不包括这个节点(因为父节点还有左子节点)
另外第三种情况移动继任者时 我们还需要再分割的节点处保持正确的顺序
findmin函数就不断对左子树进行循环取最小值
使用迭代器 重写__iter__()方法 采用yield记录函数目前运行的状态
完整代码
class BinarySearchTree: def __init__(self): self.root = None self.size = 0 def length(self): return self.size def __len__(self): return self.size def put(self,key,val): if self.root: self._put(key,val,self.root) else: self.root = TreeNode(key,val) self.size = self.size+1 def _put(self,key,val,currentNode): if key<currentNode.key: if currentNode.hasleftChild(): self._put(key,val,currentNode.leftChild) else: currentNode.leftChild = TreeNode(key,val,parent=currentNode) else: if currentNode.hasrightChild(): self._put(key,val,currentNode.rightChild) else: currentNode.rightChild = TreeNode(key,val,parent=currentNode) def __setitem__(self, key, value): self.put(key,value) def get(self,key): if self.root: res = self._get(key,self.root) if res: return res.payload else: return None else: return None def _get(self,key,currentNode): if not currentNode: return None elif currentNode.key ==key: return currentNode elif key <currentNode.key: return self._get(key,currentNode.leftChild) else: return self._get(key,currentNode.rightChild) def __getitem__(self, item): return self.get(item) def __contains__(self, key): if self._get(key,self.root): return True else: return False def delete(self,key): if self.size >1: nodeToRemove = self._get(key,self.root) if nodeToRemove: self.remove(nodeToRemove) self.size =self.size -1 else: raise KeyError("key not in tree") elif self.size==1 and self.root.key ==key: self.root = None self.size = self.size -1 else: raise KeyError("key not in tree") def __delitem__(self, key): self.delete(key) def spliceOut(self): if self.isLeaf(): if self.isLeftChild(): self.parent.leftChild = None else: self.parent.rightChild = None elif self.hasAnyChildren(): if self.hasLeftChild(): if self.isLeftChild(): self.parent.leftChild = self.leftChild else: self.parent.rightChild = self.leftChild self.leftChild.parent = self.parent else: self.parent.rightChild = self.leftChild self.leftChild.parent = self.parent else: if self.isLeftChild(): self.parent.leftChild = self.rightChild else: self.parent.rightChild = self.rightChild self.rightChild.parent = self.parent def __iter__(self): if self: if self.hasleftChild(): for elem in self.leftChild: yield elem yield self.key if self.hasrightChild(): for elem in self.rightChild: yield elem def findSuccessor(self): succ = None if self.hasrightChild(): succ = self.rightChild.findMin() else: if self.parent: if self.isLeftChild(): succ = self.parent else: self.parent.rightChild = None succ = self.parent.findSuccessor() self.parent.rightChild = self return succ def findMin(self): current = self while current.hasleftChild(): current = current.leftChild return current def remove(self,currentNode): if currentNode.isLeaf(): if currentNode ==currentNode.parent.leftChild: currentNode.parent.leftChild =None else: currentNode.parent.rightChild =None elif currentNode.hasBothChildren(): succ = currentNode.findSuccessor() succ.spliceOut() currentNode.key = succ.payload else: if currentNode.hasLeftChild(): if currentNode.isLeftChild(): currentNode.leftChild.parent = currentNode.parent currentNode.parent.leftChild = currentNode.leftChild elif currentNode.isRightChild(): currentNode.leftChild.parent = currentNode.parent currentNode.parent.rightChild = currentNode.leftChild else: currentNode.replaceNodeData(currentNode.leftChild.key, currentNode.leftChild.payload, currentNode.leftChild.leftChild, currentNode.leftChild.rightChild ) else: if currentNode.isLeftChild(): currentNode.rightChild.parent = currentNode.parent currentNode.parent.leftChild = currentNode.rightChild elif currentNode.isRightChild(): currentNode.rightChild.parent = currentNode.parent currentNode.parent.rightChild = currentNode.rightChild else: currentNode.replaceNodeData(currentNode.rightChild.key, currentNode.rightChild.payload, currentNode.rightChild.leftChild, currentNode.rightChild.rightChild ) class TreeNode: def __init__(self,key,val,left=None,right =None,parent =None): self.key = key self.payload = val self.leftChild=left self.rightChild = right self.parent = parent def replaceNodeData(self,key,value,lc,rc): self.key=key self.payload = value self.leftChild = lc self.rightChild = rc if self.hasleftChild(): self.leftChild.parent = self if self.hasrightChild(): self.rightChild.parent = self def hasleftChild(self): return self.leftChild def hasrightChild(self): return self.rightChild def isLeftChild(self): return self.parent and self.parent.leftChild ==self def isRightChild(self): return self.parent and self.parent.rightChild ==self def isRoot(self): return not self.parent def isLeaf(self): return not (self.rightChild or self.leftChild) def hasAnyChildren(self): return self.rightChild or self.leftChild def hasBothChildren(self): return self.rightChild and self.leftChild mytree = BinarySearchTree() mytree[3]="red" mytree[4]="blue" mytree[6]="yellow" mytree[2]="at" print(mytree.root.key) print(mytree.root.hasleftChild().key) print(mytree[2])
搜索树分析
如果键是以随机顺序加到树中的,那么当节点的数目为n时,树的高度大概会在log2n