python 算法 day6 搜索

排序与搜索

搜索的算法过程就是在一些项的集合中找到一个特定的项，搜索过程中会根据此项是否存在来给出回答True 或者False.

顺序搜索

从列表的第一项开始，我们按照初始顺序从一项移动到下一项，直到我们遍历所有的数据项。

def sequeueSearch(alist,item):
    pos = 0
    found = false
    while pos<len(alist) and not found:
        if alist[pos] == item:
            found = True
        else:
            pos = pos + 1
        return found

 

一个无序列表顺序搜索的复杂度是O（n）

如果我们假设一个列表是按递增顺序构建的  如果搜寻50这个数据 找到54比50大还没有找到 就直接可以立刻停止

def OrdersequeueSearch(alist, item):
    pos = 0
    found = false
    stop = false
    while pos < len(alist) and not found and not stop:
        if alist[pos] == item:
            found = True
        else:
            if alist[pos]>item:
                stop = True
            pos = pos + 1
        return found

 

二分法搜索

在有序列表中 我们可以直接拿出中间项来进行比较

 

def binarySearch(alist,item):
    first = 0
    last = len(alist) - 1
    found = False
    while first <= last and not found:
        print(alist)
        midpoint = (first+last)//2
        if alist[midpoint]==item:
            found =True
        else:
            if alist[midpoint]>item:
                last = midpoint-1
            else:
                first = midpoint +1
    return found

 

 分而治之的思想  用递归来实现  使用切片

def binaryDISearch(alist,item):
    if len(alist) == 0:
        return False
    else:
        midpoint = len(alist)//2
        if alist[midpoint]>item:
            binaryDISearch(alist[:midpoint],item)
        else:
            binaryDISearch(alist[midpoint+1:],item)

 

 

 散列

散列基于它的搜索算法时间复杂度为O(1) 

散列表是一种数据的集合，其中每个数据都通过特定的方式进行存储方便以后的查找，散列表中每一个位置叫做槽，能够存放一个数据项，并以从0开始递增的整数命名。 

某个数据项与在散列表中存储它的槽之间的映射叫做散列函数

第一个散列函数求余，简单地将将要存储的数据项与散列表的大小相除(h(item)=item%11)，返回余数作为这个数据项的散列值

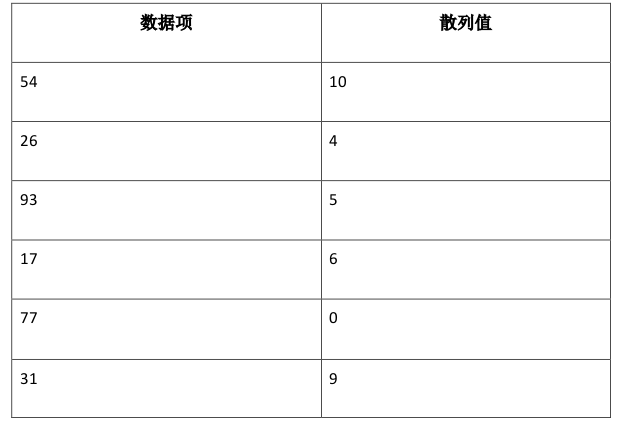
一旦求出了散列值，我们可以将每一个数据项插入到散列表中制定的位置

另外我们可以看到11个槽中的6个被占据 我们把槽被占据的比例叫做负载因子 在这个例子中 负载因子 = 数据项的个数/散列表的大小

它仅能在每一个数据项在散列表中占有不同的槽的情况下才能正常运作，不然的话会引起冲突

散列函数

对于给定一个数据项，一个散列函数可以将每一个数据项都映射到不同的槽中，那么这样的散列函数叫做完美散列函数

如果给定任意一组数据项，就没有一个系统化的方法来构造完美散列函数

 折叠法创造散列函数的基本步骤：

首先将数据分成相同长度的片段（可能最后一个片段长度不等），接着将这些片段相加，再求余得到其散列值

列如：电话号码436-555-4601，我们可以分成5段（43,65,55,46,01），然后相加得到，假设散列表有11个槽  我们就需要将和进行求余

（43+64+55+46+01）%11 = 10

创建散列函数的数值方法平方取中法

首先将数据取平方，然后取平方数的某一部分 列如数据项是44， 44的平方是1936，接着取出中间的两位数93，在进行求余计算

 

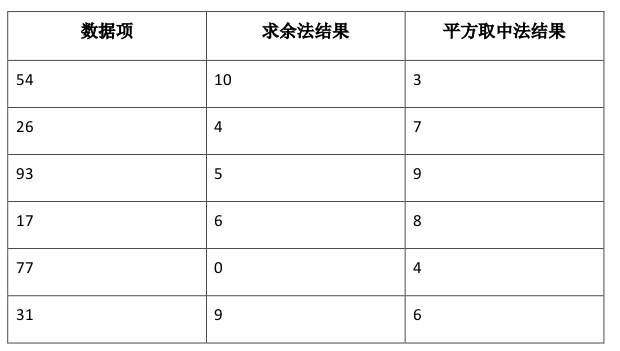
散列函数可以采用很多种方法，但必须足够高效。

 冲突解决方法

当两个数据散列到相同的槽中，我们必须用一种系统化的方法将第二个数据放到散列表中，这个过程叫做冲突解决

 一种简单的方法就是搜索散列表并寻找一个空的槽来存放这个冲突的数据，从发生冲突位置开始顺序向下继续寻找，直到我们遇到第一个空的槽，注意到我们可能需要来循环实现覆盖整个散列表，这种冲突解决方法叫做开放地址，它试图在散列表中去寻找下一个空的槽，通过系统地向后搜素每一个槽，我们将这种实现开放地址的技术叫做线性探测。

 

 

0	1	2	3	4	5	6	7	8	9	10
77				26	93	17			31	54
44									20
55

 

 

 

 利用线性探测解决冲突

如果我们寻找20，现在散列值是9,但是槽9现在存放的是31。这时我们不能单地返回假,因为我们知道这可能存在冲突。现在我们需要进行线性搜索,从槽10开始,直到我们找到数据20或者找到一个空槽。

 

线性探测的缺点：数据会在表中聚集，这意味着同一槽产生了许多冲突时 ，周边的一系列槽都会被线性探测填充，这将会对正在被填入的新数据产生影响

 

一种解决集中问题的方法 我们不再按顺序寻找空缺的槽，而是跳过一些槽，更加平均分配出现冲突的数据，

二次探测法：我们不是每次在冲突中选择跳过固定个数的槽,而是使用一个再散列函数使每次跳过槽的数量会依次增加1,3,5,7,9

 

 我们通过运用两个列表来创造一个散列表类来实现映射的数据结构

其中的一个称为slot槽 用来存储秘钥，另一个平行列表称作data 用来存储数据值

class HashTable:
    def __init__(self):
        self.size = 11
        self.slots = [None] * self.size
        self.data = [None] * self.size
    def put(self,key,data):
        hashvalue = self.hashfunction(key,len(self.slots))
        if self.slots[hashvalue] ==None:
            self.slots[hashvalue] = key
            self.data[hashvalue] = data
        else:
            if self.slots[hashvalue] == key:
                self.data[hashvalue] = data
            else:
                nextslot = self.rehash(hashvalue,len(self.slots))
                while self.slots[nextslot] !=None and self.slots[nextslot]!=key:
                    nextslot = self.rehash(nextslot,len(self.slots))
                if self.slots[nextslot] ==None:
                    self.slots[nextslot]=key
                    self.data[nextslot]=data
                else:
                    self.data[nextslot]=data
    def hashfunction(self,key,size):  #采用取余的方法
        return key%size

    def rehash(self,oldhash,size):
        return (oldhash+1)%size  #解决冲突 采用+1的线性探测
    def get(self,key):
        startslot = self.hashfunction(key,len(self.slots))
        data = None
        stop = False
        found = False
        position = startslot
        while self.slots[position] != None and not found and not stop:
            if self.slots[position]==key:
                found = True
                data = self.data[position]
            else:
                position = self.rehash(position,len(self.slots))
                if position == startslot:
                    stop = True
        return data
    def __getitem__(self, key):#重载__getitem__和__setitem__允许[]对字典进行访问
        return self.get(key)
    def __setitem__(self, key, value):
        self.key =key
        self.data =value
H = HashTable()
H[54] = "cat"
print(H.data)