SAS学习 day2

双变量分析

中心极限定理：

n个随机变量相互独立，并且服从同一个分布

 

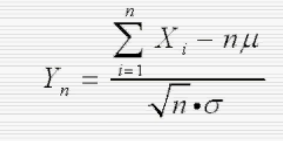
当N趋近无穷大时服从标准正态分布

应用：对一个任意的总体，在重复多次（样本量相同）抽取，且每次抽取的样本量足够大时，其抽样的均值近似服从正态分布

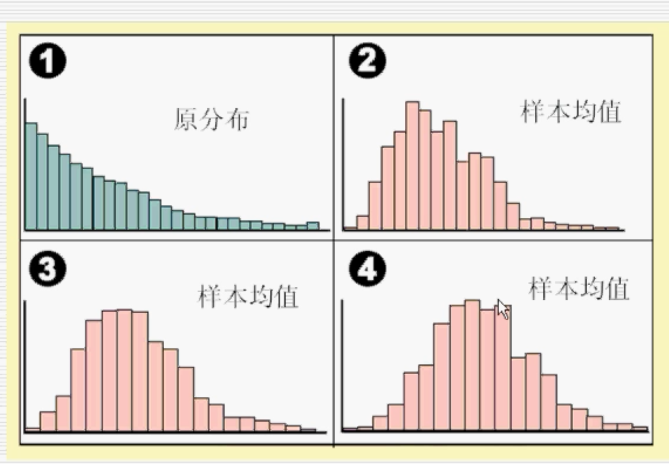
s为每个样本对应的标准差

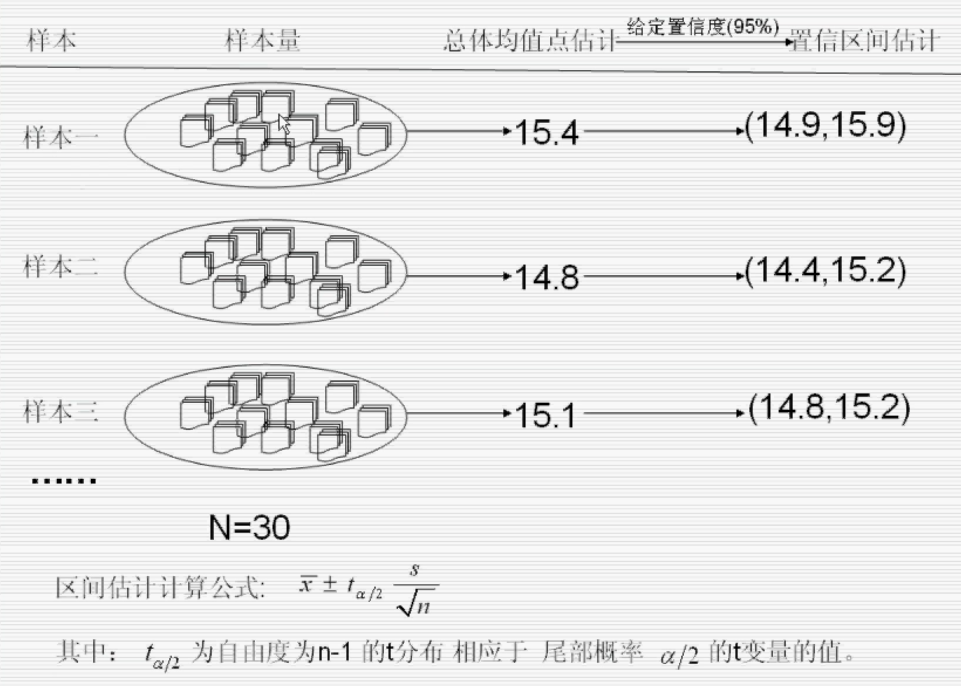
95%的置信区间：在100个类似的区间估计中，大约有95个区间能套住总体均值

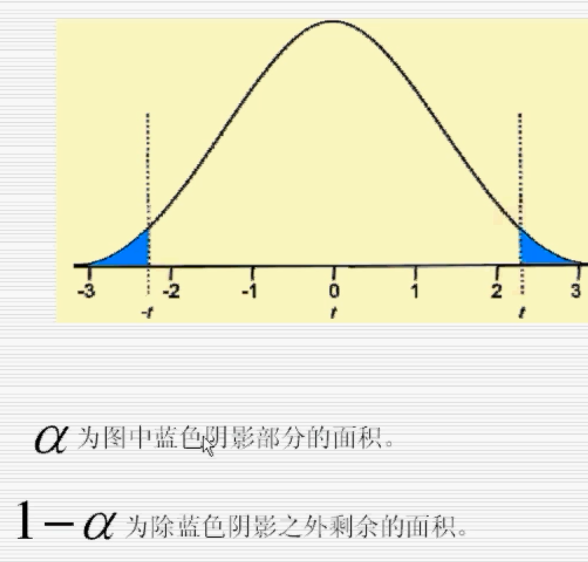
 置信度95%    alpha = 0.05 样本量越大 置信区间越小

如果固定置信区间长度，样本量越大，置信度就越大

 给定置信度，置信区间并不是唯一的 上面的概率仅是双尾概率相等时对应的置信区间

 

proc means data = Double.b_rise n mean stderr clm;   #clm置信区间
var weight;
title"95% 置信区间";
run;

 

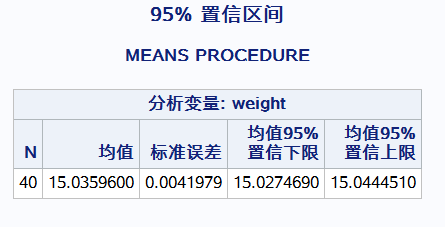
这个均值是总体均值的一个点估计 标准误差 ：s/根号下n

假设检验

设总体X服从某一分布，但是分布完全未知或部分未知，对未知总体分布所做的假设称为统计假设

参数假设 ： 已知分布，但未知分布中的参数（均值、方差）

非参数假设：未知分布或分布特征

原假设（零假设）（H0）：一般是一个保守假设，其动机是要在现实样本数据中寻找证据来推翻此假设，目的是要以比较大的可能性接受备选假设

备选假设（H1）：是原假设的对立假设

假设检验的基本思想：

　　1、反证法：首先假设H0成立，然后去寻找证据去推翻H0，并给出推翻H0所犯错误的概率

　　2、小概率原理：如果我们有足够大的概率接受备选假设，我们也可以拒绝原假设

状态	检验结果
	拒绝H0	不能拒绝H0
H0为真	第一类错误	正确
H1为真	正确	第二类错误

几点注意

1、零假设和备选假设在客观上只有一个正确，这是确定的，没有概率可言，之所以犯错误，是因为我们所面对的数据是样本而不是总体

2、第一类错误：在零假设正确时拒绝，如果小概率事件发生，于是相信数据拒绝零假设

3、P_value:拒绝零假设所犯的第一类错误 p值大 不能拒绝原假设  p值小 拒绝原假设

假设总体均值等于15 对weight进行p检验  

 

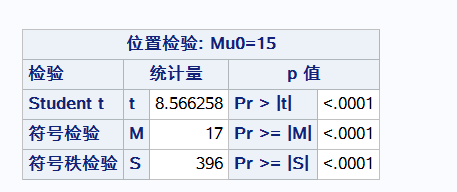
 不能肯定wight的均值等于15  犯错误概率小于0.05