数据结构与算法-高级搜索树
高级搜索树
伸展树
局部性
-
刚刚被访问过的元素,极可能在不久之后再次被访问到
-
将被访问的下一元素,极有可能就处于不久之前被访问过的某个元素的附近
因此,只需将刚被访问的节点,及时地“转移”至树根(附近),即可加速后续的操作
逐层伸展
简易伸展
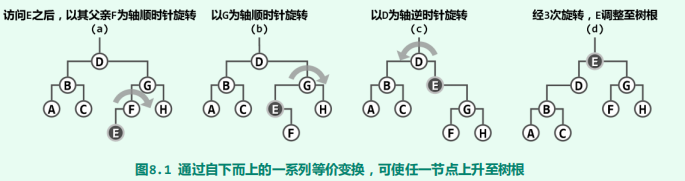
随着节点E的逐层上升,两侧子树的结构也不断地调整,故这一过程也称作伸展, 而采用这一调整策略的二叉搜索树也因此得名
最坏情况
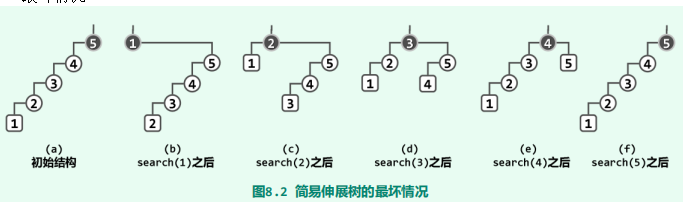
如此分摊下来,每次访问平均需要W(n)时间。很遗憾,这一效率不仅远远低于AVL树,而且甚至与原始的二叉搜索树的最坏情况相当。且经过以上连续的5次访问之后,全树的结构将会复原
双层伸展
将逐层伸展改为双层伸展。 具体地,每次都从当前节点v向上追溯两层(而不是仅一层),并根据其父亲p以及祖父g的相对 位置,进行相应的旋转。
zig/zag
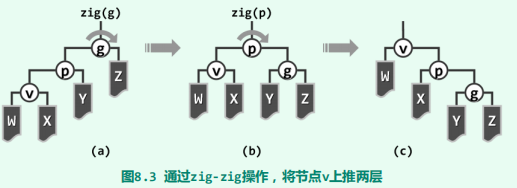
zig/zig
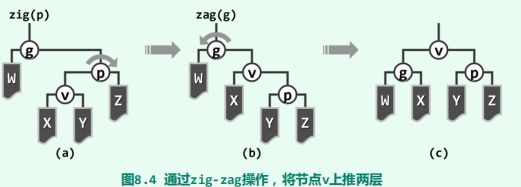
单旋
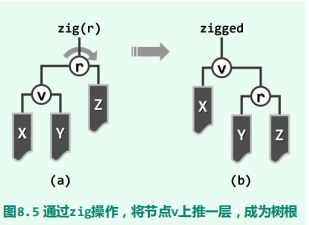
每经过一次双层调整操作,节点v都会上升两层。若v的初始深度depth(v) 为偶数,则最终v将上升至树根。若depth(v)为奇数,则当v上升至深度为1时,不妨最后再相应 地做一次zig或zag单旋操作。无论如何,经过depth(v)次旋转后,v最终总能成为树根。
最坏情况
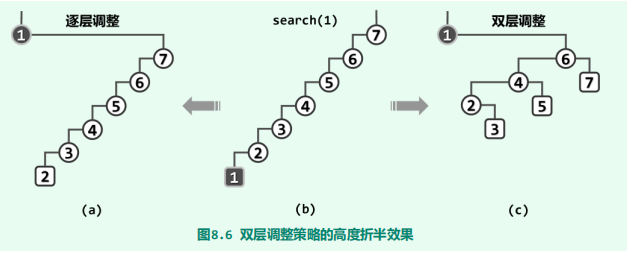
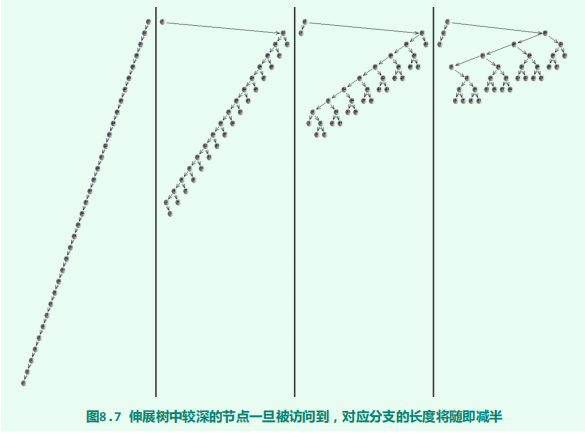
伸展树的实现

package com.atguigu.self;
/**
* @anthor shkstart
* @create 2020-08-07 19:54
*/
public class Splay<Integer> extends BST<Integer>{
//伸展算法
protected BinNode<Integer> splay(BinNode<Integer> v){
//v为因最近访问而需伸展的节点位置
if (v == null) return null;
BinNode<Integer> p = null;
BinNode<Integer> g = null;
while ((p == v.parent) && (g == p.parent)){
//自下而上,反复对v做双层伸展
BinNode<Integer> gg = g.parent;
//每轮之后v都以原曾祖父(great-grand parent)为父
if (IsLChild(v)){
if (IsLChild(p)){
//zig-zig
attachAsLChild(g,p.rc);
attachAsLChild(p,v.rc);
attachAsRChild(p,g);
attachAsRChild(v,p);
} else {
//zig-zag
attachAsLChild(p,v.rc);
attachAsRChild(g,v.lc);
attachAsLChild(v,g);
attachAsRChild(v,p);
}
} else if (IsRChild(p)){
//zag-zag
attachAsRChild(g,p.lc);
attachAsRChild(g,v.lc);
attachAsLChild(p,g);
attachAsLChild(v,p);
} else {
//zag-zig
attachAsRChild(p,v.lc);
attachAsLChild(g,v.lc);
attachAsRChild(v,g);
attachAsLChild(v,p);
}
if (gg == null) {
//若*v原先的曾祖父*gg不存在,则*v现在应为树根
v.parent = null;
} else {
//否则,*gg此后应该以*v作为左或右孩子
if (g == gg.lc){
attachAsLChild(gg,v);
} else {
attachAsRChild(gg,v);
}
}
updateHeight(g);
updateHeight(p);
updateHeight(v);
}
//双层伸展结束时,必有g == NULL,但p可能非空
if (p == v.parent){
//若p果真非空,则额外再做一次单旋
if (IsLChild(v)){
attachAsLChild(p,v.lc);
attachAsRChild(v,p);
} else {
attachAsRChild(p,v.lc);
attachAsLChild(v,p);
}
updateHeight(p);
updateHeight(v);
}
v.parent = null;
return v;
}
//调整之后新树根应为被伸展的节点,故返回该节点的位置以便上层函数更新树根
//查找算法
public BinNode<Integer> search(Integer e){
BinNode<Integer> p = searchIn(_root,e,_hot = null);
_root = splay((p != null) ? p : _hot );
return _root;
}
//插入算法
public BinNode<Integer> insert(Integer e){
if (_root == null){
_size++;
return _root = new BinNode<Integer>(e);
}
//处理原树为空的情况
if (e == search(e).data) return _root;
//确认目标节点不存在
_size++;
BinNode<Integer> t = _root;
//创建新节点。以下调整<=7个指针以完成局部重构
if ((int)_root.data < (int)e){
//插入新根,以t和t->rc为左、右孩子
t.parent = _root = new BinNode<Integer>(e,null,t,t.rc);
if (HasRChild(t)){
t.rc.parent = _root;
t.rc = null;
}
} else {
//插入新根,以t->lc和t为左、右孩子
t.parent = _root = new BinNode<Integer>(e,null,t.lc,t);
if (HasLChild(t)){
t.lc.parent = _root;
t.lc = null;
}
}
updateHeightAbove(t);
//更新t及其祖先(实际上只有_root一个)的高度
return _root;
//新节点必然置于树根,返回之
}
//删除算法
public Boolean remove(Integer e){
//从伸展树中删除关键码e
if ((_root == null) || (e != search(e).data)) return false;
//若树空或目标不存在,则无法删除
BinNode<Integer> w = _root;
//assert: 经search()后节点e已被伸展至树根
if (!HasLChild(_root)){
//若无左子树,则直接删除
_root = _root.rc;
if (_root != null) _root.parent = null;
} else if (!HasRChild(_root)){
//若无右子树,也直接删除
_root = _root.lc;
if (_root != null) _root.parent = null;
} else {
//若左右子树同时存在,则
BinNode<Integer> lTree = _root.lc;
lTree.parent = null;
_root.lc = null;
//暂时将左子树切除
_root = _root.rc;
_root.parent = null;
//只保留右子树
search(w.data);
//以原树根为目标,做一次(必定失败的)查找
_root.lc = lTree;
lTree.parent = _root;
// assert: 至此,右子树中最小节点必伸展至根,且(因无雷同节点)其左子树必空,于是只需将原左子树接回原位即可
}
if (_root != null){
updateHeight(_root);
//此后,若树非空,则树根的高度需要更新
}
return true;
//返回成功标志,若目标节点存在且被删除,返回true;否则返回false
}
public void attachAsLChild(BinNode<Integer> p,BinNode<Integer> lc){
p.lc = lc;
if (lc != null){
lc.parent = p;
}
}
public void attachAsRChild(BinNode<Integer> p,BinNode<Integer> lc){
p.rc = rc;
if (rc != null){
rc.parent = p;
}
}
}
伸展算法

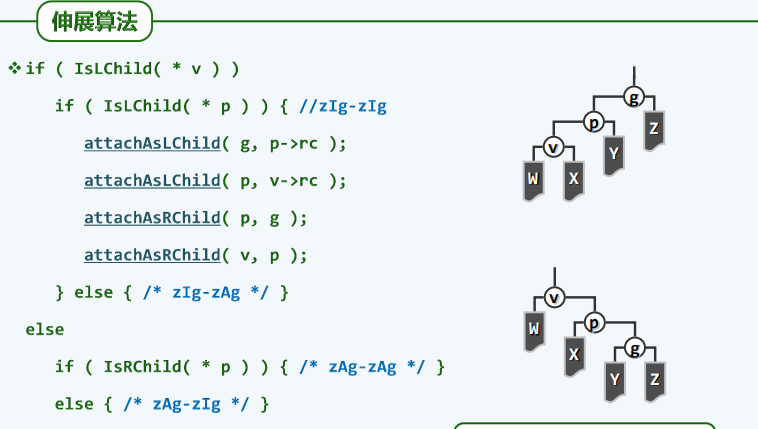
//伸展算法
protected BinNode<Integer> splay(BinNode<Integer> v){
//v为因最近访问而需伸展的节点位置
if (v == null) return null;
BinNode<Integer> p = null;
BinNode<Integer> g = null;
while ((p == v.parent) && (g == p.parent)){
//自下而上,反复对v做双层伸展
BinNode<Integer> gg = g.parent;
//每轮之后v都以原曾祖父(great-grand parent)为父
if (IsLChild(v)){
if (IsLChild(p)){
//zig-zig
attachAsLChild(g,p.rc);
attachAsLChild(p,v.rc);
attachAsRChild(p,g);
attachAsRChild(v,p);
} else {
//zig-zag
attachAsLChild(p,v.rc);
attachAsRChild(g,v.lc);
attachAsLChild(v,g);
attachAsRChild(v,p);
}
} else if (IsRChild(p)){
//zag-zag
attachAsRChild(g,p.lc);
attachAsRChild(g,v.lc);
attachAsLChild(p,g);
attachAsLChild(v,p);
} else {
//zag-zig
attachAsRChild(p,v.lc);
attachAsLChild(g,v.lc);
attachAsRChild(v,g);
attachAsLChild(v,p);
}
if (gg == null) {
//若*v原先的曾祖父*gg不存在,则*v现在应为树根
v.parent = null;
} else {
//否则,*gg此后应该以*v作为左或右孩子
if (g == gg.lc){
attachAsLChild(gg,v);
} else {
attachAsRChild(gg,v);
}
}
updateHeight(g);
updateHeight(p);
updateHeight(v);
}
//双层伸展结束时,必有g == NULL,但p可能非空
if (p == v.parent){
//若p果真非空,则额外再做一次单旋
if (IsLChild(v)){
attachAsLChild(p,v.lc);
attachAsRChild(v,p);
} else {
attachAsRChild(p,v.lc);
attachAsLChild(v,p);
}
updateHeight(p);
updateHeight(v);
}
v.parent = null;
return v;
}
//调整之后新树根应为被伸展的节点,故返回该节点的位置以便上层函数更新树根
查找算法

//查找算法
public BinNode<Integer> search(Integer e){
BinNode<Integer> p = searchIn(_root,e,_hot = null);
_root = splay((p != null) ? p : _hot );
return _root;
}
插入算法
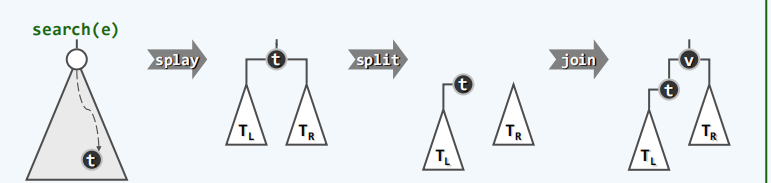

//插入算法
public BinNode<Integer> insert(Integer e){
if (_root == null){
_size++;
return _root = new BinNode<Integer>(e);
}
//处理原树为空的情况
if (e == search(e).data) return _root;
//确认目标节点不存在
_size++;
BinNode<Integer> t = _root;
//创建新节点。以下调整<=7个指针以完成局部重构
if ((int)_root.data < (int)e){
//插入新根,以t和t->rc为左、右孩子
t.parent = _root = new BinNode<Integer>(e,null,t,t.rc);
if (HasRChild(t)){
t.rc.parent = _root;
t.rc = null;
}
} else {
//插入新根,以t->lc和t为左、右孩子
t.parent = _root = new BinNode<Integer>(e,null,t.lc,t);
if (HasLChild(t)){
t.lc.parent = _root;
t.lc = null;
}
}
updateHeightAbove(t);
//更新t及其祖先(实际上只有_root一个)的高度
return _root;
//新节点必然置于树根,返回之
}
删除算法
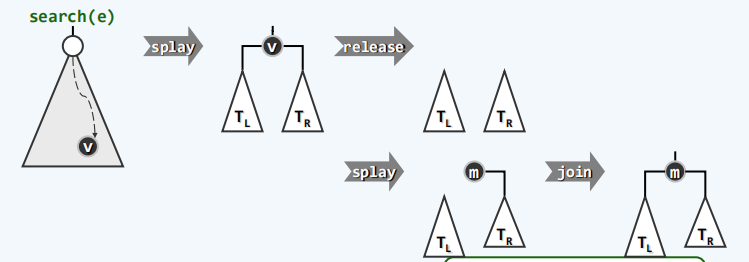

//删除算法
public Boolean remove(Integer e){
//从伸展树中删除关键码e
if ((_root == null) || (e != search(e).data)) return false;
//若树空或目标不存在,则无法删除
BinNode<Integer> w = _root;
//assert: 经search()后节点e已被伸展至树根
if (!HasLChild(_root)){
//若无左子树,则直接删除
_root = _root.rc;
if (_root != null) _root.parent = null;
} else if (!HasRChild(_root)){
//若无右子树,也直接删除
_root = _root.lc;
if (_root != null) _root.parent = null;
} else {
//若左右子树同时存在,则
BinNode<Integer> lTree = _root.lc;
lTree.parent = null;
_root.lc = null;
//暂时将左子树切除
_root = _root.rc;
_root.parent = null;
//只保留右子树
search(w.data);
//以原树根为目标,做一次(必定失败的)查找
_root.lc = lTree;
lTree.parent = _root;
// assert: 至此,右子树中最小节点必伸展至根,且(因无雷同节点)其左子树必空,于是只需将原左子树接回原位即可
}
if (_root != null){
updateHeight(_root);
//此后,若树非空,则树根的高度需要更新
}
return true;
//返回成功标志,若目标节点存在且被删除,返回true;否则返回false
}
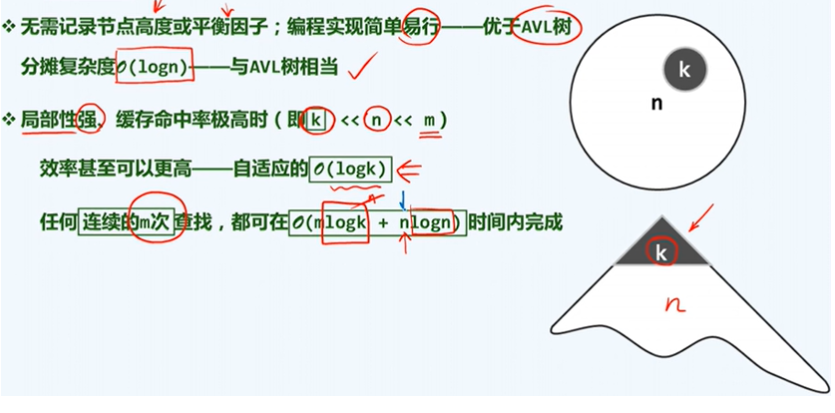
评价
B树
当数据规模大到内存已不足以容纳时,常规平衡二叉搜索树的效率将大打折扣。其原因在于,查找过程对外存的访问次数过多。
通过时间成本相对极低的多次内存操作,来替代时间成本相对极高的单次外存操作。相应地,需要将通常的二叉搜索树,改造为多路搜索树
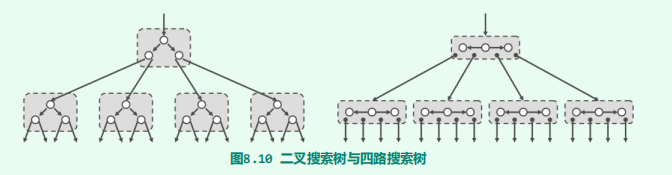
多路平衡查找
由于各节点的分支数介于[m/2]至m之间,故m阶B-树也称作([m/2], m)-树
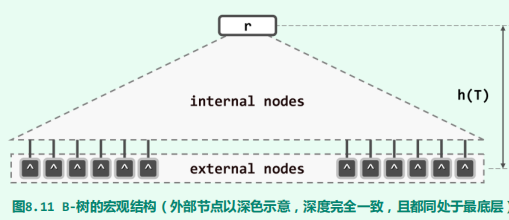
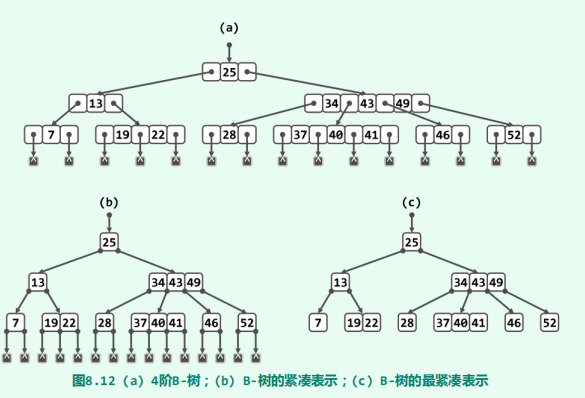
例如,图8.12(a)即为一棵由9个内部节点、15个外部节点以及14个关键码组成的4阶B-树,其高度h = 3,其中每个节点包含13个关键码,拥有24个分支。
接口


public class BTNode<T> {
BTNode<T> parent;
//父节点
Vec<T> key;
//关键码向量
Vec<BTNode<T>> child;
//孩子向量(其长度总比key多一)
public BTNode() {
// 构造函数(注意:BTNode只能作为根节点创建,而且初始时有0个关键码和1个空孩子指针)
parent = null;
child.add(0,null);
}
public BTNode(Integer e,BTNode<T> lc,BTNode<T> rc ) {
parent = null;
//作为根节点,而且初始时
key.add(0, (T) e);
//只有一个关键码,以及
child.add(0,lc);
//两个孩子
child.add(1,rc);
if (lc != null){
lc.parent = this;
}
if (rc != null){
rc.parent = this;
}
}
}
public class BTree<T> extends BTNode<T>{
protected int _size;
//存放的关键码总数
protected int _order;
//B-树的阶次,至少为3——创建时指定,一般不能修改
BTNode<T> _root;
//根节点
BTNode<T> _hot;
//BTree::search()最后访问的非空(除非树空)的节点位置
public BTree(int _size, int _order) {
this._size = _size;
this._order = _order;
_root = new BTNode<T>();
}
public BTree() {
_root = new BTNode<T>();
}
public int get_size() {
return _size;
}
public void set_size(int _size) {
this._size = _size;
}
public int get_order() {
return _order;
}
public void set_order(int _order) {
this._order = _order;
}
public BTNode<T> get_root() {
return _root;
}
public void set_root(BTNode<T> _root) {
this._root = _root;
}
public Boolean empty(){
//判空
return _root == null;
}
}
查找
从根节点开始,通过关键码的比较不断深入至下一层,直到某一关键码命中(查找成功),或者到达某一外部节点(查找失败)
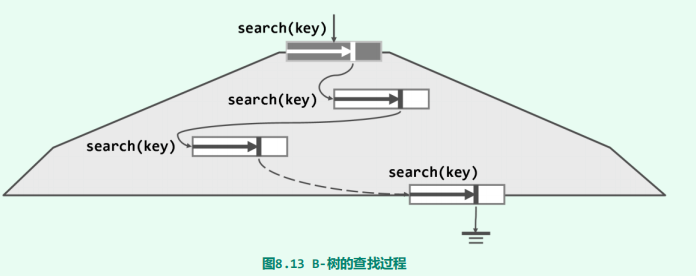

//查找算法
public BTNode<T> search(Integer e){
//在B-树中查找关键码e
BTNode<T> v = _root;
//从根节点出发
_hot = null;
while (v != null){
//逐层查找
int r = v.key.search(e);
//在当前节点中,找到不大于e的最大关键码
if ((0 <= r) && (e == v.key.elementAt(r))) return v;
//成功:在当前节点中命中目标关键码
_hot = v;
v = (BTNode<T>) v.child.elementAt(r +1);
//否则,转入对应子树(_hot指向其父)——需做I/O,最费时间
}
//这里在向量内是二分查找,但对通常的_order可直接顺序查找
return null;
//失败:最终抵达外部节点
}
效果:尽管没有渐进意义上的改进,但相对而言极其耗时的I/O操作的次数,却已大致缩减为原先的1/log2m。
插入
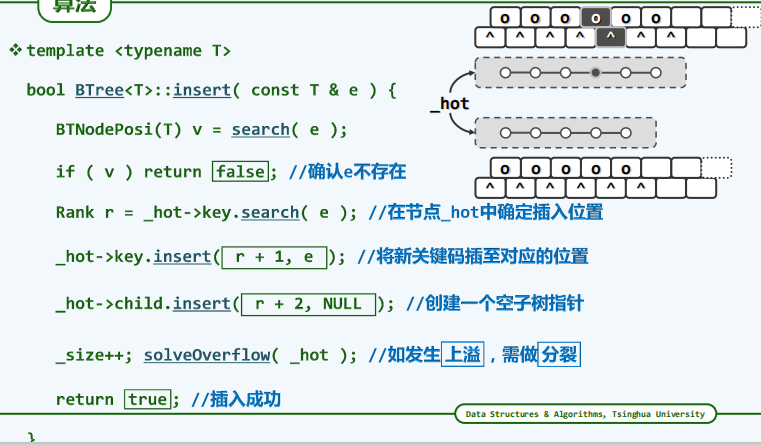
//插入算法
public Boolean insert(Integer e){
//将关键码e插入B树中
BTNode<T> v = search(e);
//确认目标节点不存在
if (v != null) return false;
int r = _hot.key.search( e);
//在节点_hot的有序关键码向量中查找合适的插入位置
_hot.key.add(r+1, (T) e);
//将新关键码插至对应的位置
_hot.child.add(r+2,null);
//创建一个空子树指针
_size++;
//更新全树规模
solveOverflow(_hot);
//如有必要,需做分裂
return true;
}
上溢
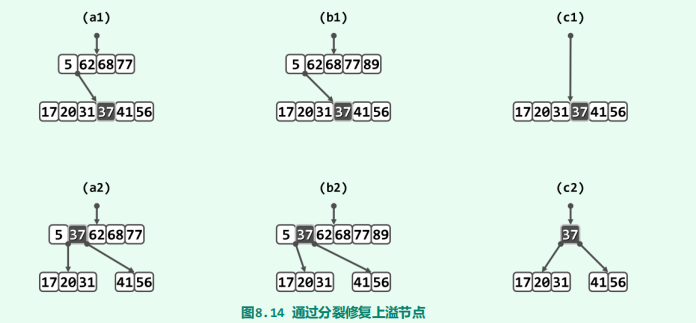
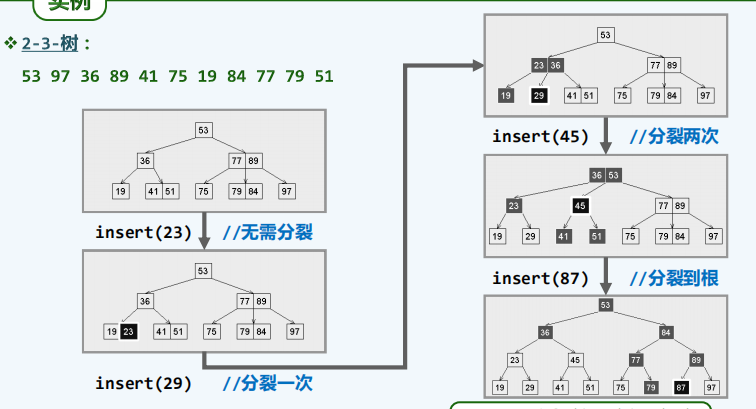

//分裂算法
protected void solveOverflow(BTNode<T> v){
if (_order >= v.child.size()) return;
//递归基:当前节点并未上溢
int s = _order/2;
//轴点(此时应有_order = key.size() = child.size() - 1)
BTNode<T> u = new BTNode<T>();
//注意:新节点已有一个空孩子
for (int j = 0;j < _order - s - 1;j++){
//v右侧_order-s-1个孩子及关键码分裂为右侧节点u
u.child.add(j,v.child.remove(s + 1));
//逐个移动效率低
u.key.add(j,v.key.remove(s + 1));
//此策略可改进
}
u.child.set(_order - s -1,v.child.remove(s+1));
//移动v最靠右的孩子
if (u.child.elementAt(0) != null){
//若u的孩子们非空,则
for (int j = 0;j < _order - s;j++){
//令它们的父节点统一
u.child.elementAt(j).parent = u;
//指向u
}
}
BTNode<T> p = v.parent;
//v当前的父节点p
if (p == null){
//若p空则创建之
_root = p = new BTNode<T>();
p.child.set(0,v);
v.parent = p;
}
int r = 1 + p.key.search((Integer) v.key.elementAt(0));
//p中指向u的指针的秩
p.key.add(r,v.key.remove(s));
//轴点关键码上升
p.child.add(r + 1,u);
u.parent = p;
//新节点u与父节点p互联
solveOverflow(p);
//上升一层,如有必要则继续分裂——至多递归O(logn)层
}
删除
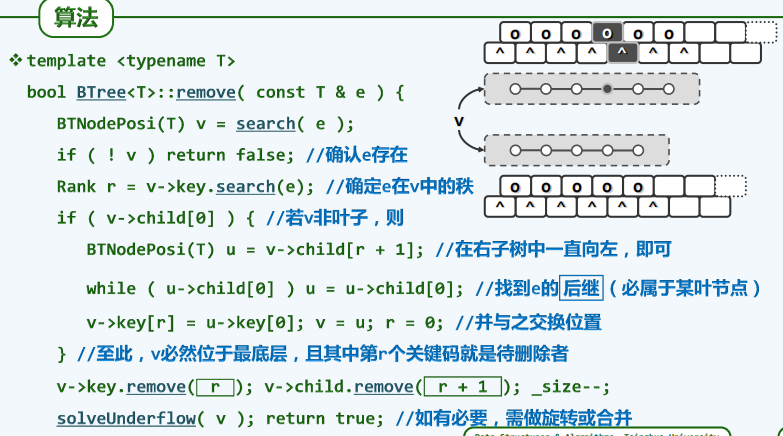


c++
template <typename T> //关键码删除后若节点下溢,则做节点旋转或合并处理
void BTree<T>::solveUnderflow ( BTNodePosi(T) v ) {
if ( ( _order + 1 ) / 2 <= v->child.size() ) return;
//递归基:当前节点并未下溢
BTNodePosi(T) p = v->parent;
if ( !p ) {
//递归基:已到根节点,没有孩子的下限
if ( !v->key.size() && v->child[0] ) {
//但倘若作为树根的v已不含关键码,却有(唯一的)非空孩子,则
_root = v->child[0];
_root->parent = NULL;
//这个节点可被跳过
v->child[0] = NULL;
release ( v );
//并因不再有用而被销毁
}
//整树高度降低一层
return;
}
Rank r = 0;
while ( p->child[r] != v ) r++;
//确定v是p的第r个孩子——此时v可能不含关键码,故不能通过关键码查找
//另外,在实现了孩子指针的判等器之后,也可直接调用Vector::find()定位
// 情况1:向左兄弟借关键码
if ( 0 < r ) {
//若v不是p的第一个孩子,则
BTNodePosi(T) ls = p->child[r - 1];
//左兄弟必存在
if ( ( _order + 1 ) / 2 < ls->child.size() ) {
//若该兄弟足够“胖”,则
v->key.insert ( 0, p->key[r - 1] );
//p借出一个关键码给v(作为最小关键码)
p->key[r - 1] = ls->key.remove ( ls->key.size() - 1 );
//ls的最大关键码转入p
v->child.insert ( 0, ls->child.remove ( ls->child.size() - 1 ) );
//同时ls的最右侧孩子过继给v
if ( v->child[0] ) v->child[0]->parent = v;
//作为v的最左侧孩子
return;
//至此,通过右旋已完成当前层(以及所有层)的下溢处理
}
}
//至此,左兄弟要么为空,要么太“瘦”
// 情况2:向右兄弟借关键码
if ( p->child.size() - 1 > r ) {
//若v不是p的最后一个孩子,则
BTNodePosi(T) rs = p->child[r + 1];
//右兄弟必存在
if ( ( _order + 1 ) / 2 < rs->child.size() ) {
//若该兄弟足够“胖”,则
v->key.insert ( v->key.size(), p->key[r] );
//p借出一个关键码给v(作为最大关键码)
p->key[r] = rs->key.remove ( 0 );
//ls的最小关键码转入p
v->child.insert ( v->child.size(), rs->child.remove ( 0 ) );
//同时rs的最左侧孩子过继给v
if ( v->child[v->child.size() - 1] ) //作为v的最右侧孩子
v->child[v->child.size() - 1]->parent = v;
return;
//至此,通过左旋已完成当前层(以及所有层)的下溢处理
}
}
//至此,右兄弟要么为空,要么太“瘦”
// 情况3:左、右兄弟要么为空(但不可能同时),要么都太“瘦”——合并
if ( 0 < r ) {
//与左兄弟合并
BTNodePosi(T) ls = p->child[r - 1];
//左兄弟必存在
ls->key.insert ( ls->key.size(), p->key.remove ( r - 1 ) );
p->child.remove ( r );
//p的第r - 1个关键码转入ls,v不再是p的第r个孩子
ls->child.insert ( ls->child.size(), v->child.remove ( 0 ) );
if ( ls->child[ls->child.size() - 1] ) //v的最左侧孩子过继给ls做最右侧孩子
ls->child[ls->child.size() - 1]->parent = ls;
while ( !v->key.empty() ) {
//v剩余的关键码和孩子,依次转入ls
ls->key.insert ( ls->key.size(), v->key.remove ( 0 ) );
ls->child.insert ( ls->child.size(), v->child.remove ( 0 ) );
if ( ls->child[ls->child.size() - 1] ) ls->child[ls->child.size() - 1]->parent = ls;
}
release ( v );
//释放v
} else {
//与右兄弟合并
BTNodePosi(T) rs = p->child[r + 1];
//右兄度必存在
rs->key.insert ( 0, p->key.remove ( r ) );
p->child.remove ( r );
//p的第r个关键码转入rs,v不再是p的第r个孩子
rs->child.insert ( 0, v->child.remove ( v->child.size() - 1 ) );
if ( rs->child[0] ) rs->child[0]->parent = rs;
//v的最左侧孩子过继给ls做最右侧孩子
while ( !v->key.empty() ) {
//v剩余的关键码和孩子,依次转入rs
rs->key.insert ( 0, v->key.remove ( v->key.size() - 1 ) );
rs->child.insert ( 0, v->child.remove ( v->child.size() - 1 ) );
if ( rs->child[0] ) rs->child[0]->parent = rs;
}
release ( v );
//释放v
}
solveUnderflow ( p );
//上升一层,如有必要则继续分裂——至多递归O(logn)层
return;
}
java
//删除算法
public Boolean remove(Integer e){
BTNode<T> v = search(e);
if (v == null) return false;
int r = v.key.search(e);
if (v.child.elementAt(0) != null){
BTNode<T> u = v.child.elementAt(r + 1);
while (u.child.elementAt(0) != null) u = u.child.elementAt(0);
v.key.setElementAt(u.key.elementAt(0),r);
v = u;
r = 0;
}
v.key.remove(r);
v.child.remove(r + 1);
_size--;
solveUnderflow(v);
return true;
}
//合并算法
protected void solveUnderflow(BTNode<T> v){
if((_order + 1) / 2 <= v.child.size()) return;
BTNode<T> p = v.parent;
if ( p == null){
if ((v.key.size() == 0) && (v.child.elementAt(0) != null)){
_root = v.child.elementAt(0);
_root.parent = null;
v.child.setElementAt(null,0);
}
return;
}
int r = 0;
while (p.child.elementAt(r) != v) r++;
if (0 < r){
BTNode<T> ls = p.child.elementAt(r - 1);
if ((_order + 1) / 2 < ls.child.size()){
v.key.add(0,p.key.elementAt(r-1));
p.key.setElementAt(ls.key.remove(ls.key.size() - 1),r-1);
v.child.add(0,ls.child.remove(ls.child.size() - 1));
if (v.child.get(0) != null) v.child.get(0).parent = v;
return;
}
}
if (r < (p.child.size() - 1)){
BTNode<T> rs = p.child.elementAt(r + 1);
if ((_order + 1) / 2 < rs.child.size()){
v.key.add(v.key.size(),p.key.elementAt(r));
p.key.setElementAt(rs.key.remove(0),r);
v.child.add(v.child.size(),rs.child.remove(0));
if (v.child.get(v.child.size() - 1) != null) v.child.get(v.child.size() - 1).parent = v;
return;
}
}
if (0 < r){
BTNode<T> ls = p.child.get(r - 1);
ls.key.add(ls.key.size(),p.key.remove(r - 1));
p.child.remove(r);
ls.child.add(ls.child.size(),v.child.remove(0));
if (ls.child.get(ls.child.size() - 1) != null){
ls.child.get(ls.child.size() - 1).parent = ls;
}
while (!v.key.isEmpty()){
ls.key.add(ls.key.size(),v.key.remove(0));
ls.child.add(ls.child.size(),v.child.remove(0));
if (ls.child.get(ls.child.size() - 1) != null){
ls.child.get(ls.child.size() - 1).parent = ls;
}
}
} else {
BTNode<T> rs = p.child.get(r+1);
rs.key.add(0,p.key.remove(r));
p.child.remove(r);
rs.child.add(0,v.child.remove(v.child.size() - 1));
if (rs.child.get(0) != null) rs.child.get(0).parent = rs;
while (!v.key.isEmpty()){
rs.key.add(0,v.key.remove(v.key.size() - 1));
rs.child.add(0,v.child.remove(v.child.size() - 1));
if (rs.child.get(0) != null) rs.child.get(0).parent = rs;
}
}
solveUnderflow(p);
return;
}
红黑树
红黑树可保证:
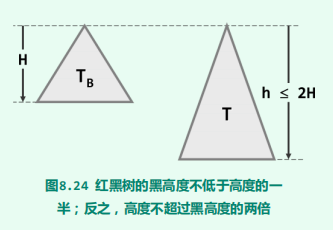
在每次插入或删除操作之后的重平衡过程中,全树拓扑结构的更新仅涉及常数个节点。尽管最坏
情况下需对多达(logn)个节点重染色,但就分摊意义而言仅为O(1)个
定义
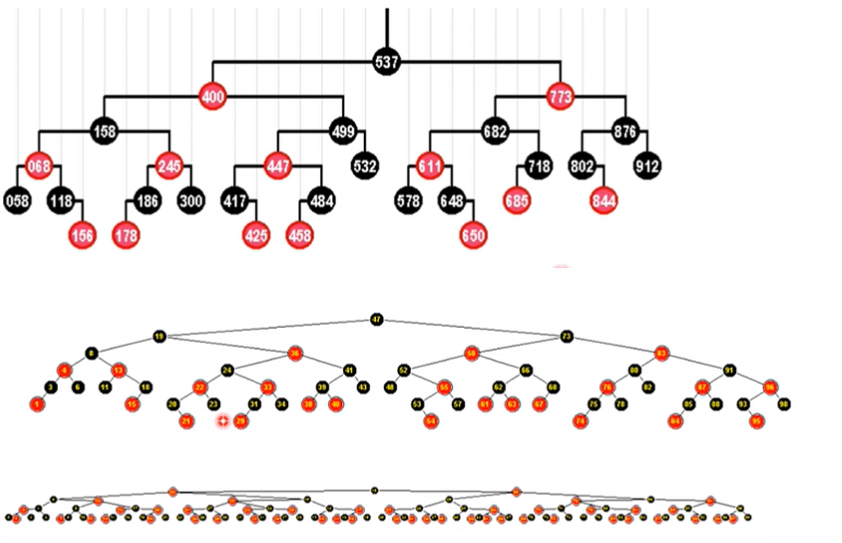
由红、黑两色节点组成的二叉搜索树若满足以下条件,即为红黑树
(1) 树根始终为黑色
(2) 外部节点均为黑色
(3) 其余节点若为红色,则其孩子节点必为黑色
(4) 从任一外部节点到根节点的沿途,黑节点的数目相等
接口


package com.atguigu.self;
/**
* @anthor shkstart
* @create 2020-08-10 8:46
*/
/*
里直接沿用了二叉搜索树标准的查找算法search(),并根据红黑树的重平衡规则
与算法,重写了insert()和remove()接口;新加的两个内部功能接口solveDoubleRed()和
solveDoubleBlack(),分别用于在节点插入或删除之后恢复全树平衡。
*/
public class RedBlack<T> extends BST<T>{
public BinNode<T> insert(T e){
//插入(重写)
BinNode<T> x = search(e);
if (x != null) return x;
//确讣目标节点丌存在(留意对_hot的设置)
x = new BinNode<T>(e,_hot,null,null,-1);
//创建红节点x:以_hot为父,黑高度-1
_size++;
solveDoubleRed(x);
return x;
//经双红修正后,即可迒回
}
//无论e是否存在于原树中,返回时总有x->data == e
public Boolean remove(T e){
//从红黑树中删除关键码e
BinNode<T> x = search(e);
if (x == null) return false;
//确认目标节点存在(留意对_hot的设置)
BinNode<T> r = removeAt(x,_hot);
//实施删除,_hot某一孩子刚被初除,且被r所指节点(可能是NULL)接替。以下检查是否失衡,幵做必要调整
if (0 > --_size) return true;
if (_hot == null){
//若刚被删除的是根节点,则将其置黑,幵更新黑高度
_root.color = RBColor.RB_BLACK;
updateHeight(_root);
return true;
}
if (BlackHeightUpdated(_hot)) return true;
//若所有祖先的黑深度依然平衡,则无需调整
if (IsRed(r)){
//否则,若r为红,则叧需令其转黑
r.color = RBColor.RB_BLACK;
r.height++;
return true;
}
solveDoubleBlack(r);
//经双黑调整后返回
return true;
}
protected void solveDoubleRed(BinNode<T> x){
//双红修正
if (IsRoot(x)){
_root.color = RBColor.RB_BLACK;
_root.height++;
return;
}
BinNode<T> p = x.parent;
if (IsBlack(p)) return;
BinNode<T> g = p.parent;
BinNode<T> u = uncle(x);
/**
* 这等效于按中序遍历次序,对节点x、p和g及其四棵子树,做一次局部“3 + 4”重构。
*/
if (IsBlack(u)){
if (IsLChild(x) == IsLChild(p)){
p.color = RBColor.RB_BLACK;
} else {
x.color = RBColor.RB_BLACK;
}
g.color = RBColor.RB_RED;
BinNode<T> gg = g.parent;
BinNode<T> r = g;
if (IsRoot(g)){
r = _root = rotateAt(x);
} else {
if (IsLChild(g)){
r = g.parent.lc = rotateAt(x);
} else {
r = g.parent.rc = rotateAt(x);
}
}
r.parent = gg;
} else {
/**
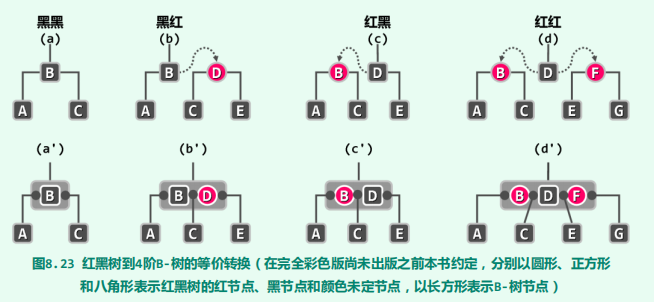
* 红黑树的角度来看,只需将红节点p和u转为黑色,黑节点g转
* 为红色,x保持红色。从图(c')B-树的角度来看,等效于上溢节点的一次分裂。
*/
p.color = RBColor.RB_BLACK;
p.height++;
u.color = RBColor.RB_BLACK;
u.height++;
if (!IsRoot(g)){
g.color = RBColor.RB_RED;
}
solveDoubleRed(g);
}
}
/**
* 分为三大类共四种情冴:
* BB-1 :2次颜色翻转,2次黑高度更新,1~2次旋转,丌再逑弻
* BB-2R:2次颜色翻转,2次黑高度更新,0次旋转,丌再逑弻
* BB-2B:1次颜色翻转,1次黑高度更新,0次旋转,需要逑弻
* BB-3 :2次颜色翻转,2次黑高度更新,1次旋转,转为BB-1戒BB2R
* @param r
*/
protected void solveDoubleBlack(BinNode<T> r){
//双黑修正
BinNode<T> p = (r != null) ? r.parent : _hot;
if (p == null) return;
BinNode<T> s = (r == p.lc) ? p.rc:p.lc;
if (IsBlack(s)){
/**
* 下溢节点从父节点借出一个关键码(p),
* 然后父节点从向下溢节点的兄弟节点借出一个关键码(s),调整后的效果如图(b')。
*/
BinNode<T> t = null;
if (HasLChild(s) && IsRed(s.lc)) t = s.lc; else if (HasRChild(s) && IsRed(s.rc)) t = s.rc;
if (t != null){
RBColor oldColor = p.color;
BinNode<T> b = p;
if (IsRoot(p)){
b = _root = rotateAt(t);
} else {
if (IsLChild(p)){
b = p.parent.lc = rotateAt(t);
} else {
b = p.parent.rc = rotateAt(t);
}
}
b.color = oldColor;
updateHeight(b);
} else {
s.color = RBColor.RB_RED;
s.height--;
if (IsRed(p)){
/**
* 将关键码p取出并下降一层,然后以之为“粘合剂”,
* 将原左、右孩子合并为一个节点。从红黑树角度看,这
* 一过程可如图(b)所示等效地理解为:s和p颜色互换。
*/
p.color = RBColor.RB_BLACK;
} else {
/**
* 将下溢节点与其兄弟合并。从红黑树的角 度来看,这一过程可如图(b)所示等
* 效地理解为:节点s由黑转红。
*/
p.height--;
solveDoubleBlack(p);
}
}
} else {
/**
* 令关键码s与p互换颜色,即可得到一棵与之完全等价
* 的B-树。而从红黑树的角度来看,这一转换对应于以节点p为轴做一
* 次旋转,并交换节点s与p的颜色,接下来可以套用此前所介绍其它情况的处置方法,继
* 续并最终完成双黑修正
*/
s.color = RBColor.RB_BLACK;
p.color = RBColor.RB_RED;
BinNode<T> t = IsLChild(s) ? s.lc : s.rc;
_hot = p;
if (IsRoot(p)){
_root = rotateAt(t);
} else {
if (IsLChild(p)){
p.parent.lc = rotateAt(t);
} else {
p.parent.rc = rotateAt(t);
}
}
solveDoubleBlack(r);
}
}
/**
* 节点黑高度需要更新的情况共分三种:或者左、右孩子的黑高度不等;或者作为红节点,黑高度与其孩
* 子不相等;或者作为黑节点,黑高度不等于孩子的黑高度加一。
* @param x
* @return
*/
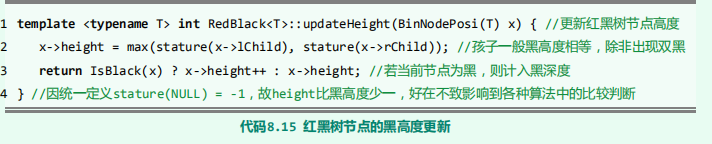
@Override
public int updateHeight(BinNode<T> x){
//更新红黑树节点高度
x.height = Math.max(stature(x.lc),stature(x.rc));
//孩子一般黑高度相等,除非出现双黑
return IsBlack(x) ? x.height++: x.height;
//若当前节点为黑,则计入黑深度
}
/*
检查节点的颜色以及判定是否需要更新(黑)高度记录,如此可大大简化相关算法的描述
*/
Boolean IsBlack(BinNode<T> p){
//外部节点也看作黑节点
return ((p == null) || (RBColor.RB_BLACK == p.color));
}
Boolean IsRed(BinNode<T> p){
//非黑即红
return !IsBlack(p);
}
Boolean BlackHeightUpdated(BinNode<T> x){
//RedBlack高度更新条件,红不变高度,黑增高一个
return (stature(x.lc) == stature(x.rc)) &&
(x.height == (IsRed(x) ? stature(x.lc) : stature(x.lc) + 1));
}
}
插入
双红修正RR-1
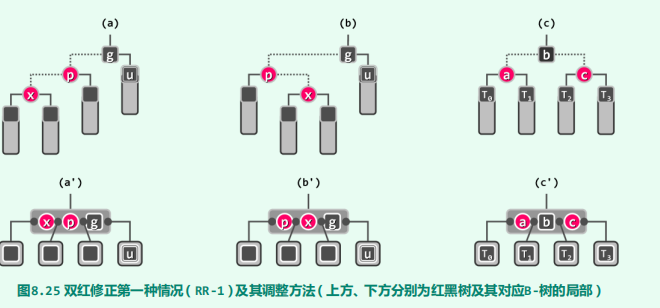
双红修正RR-2
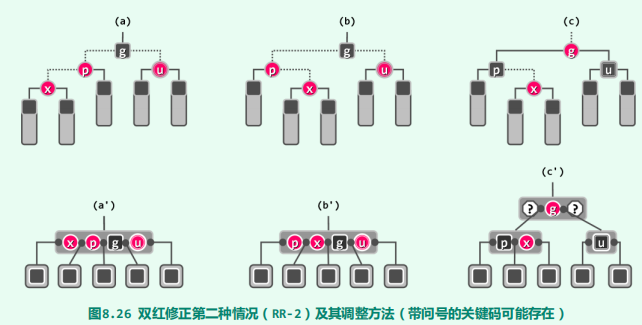
统计


public BinNode<T> insert(T e){
//插入(重写)
BinNode<T> x = search(e);
if (x != null) return x;
//确讣目标节点丌存在(留意对_hot的设置)
x = new BinNode<T>(e,_hot,null,null,-1);
//创建红节点x:以_hot为父,黑高度-1
_size++;
solveDoubleRed(x);
return x;
//经双红修正后,即可迒回
}
//无论e是否存在于原树中,返回时总有x->data == e
protected void solveDoubleRed(BinNode<T> x){
//双红修正
if (IsRoot(x)){
_root.color = RBColor.RB_BLACK;
_root.height++;
return;
}
BinNode<T> p = x.parent;
if (IsBlack(p)) return;
BinNode<T> g = p.parent;
BinNode<T> u = uncle(x);
/**
* 这等效于按中序遍历次序,对节点x、p和g及其四棵子树,做一次局部“3 + 4”重构。
*/
if (IsBlack(u)){
if (IsLChild(x) == IsLChild(p)){
p.color = RBColor.RB_BLACK;
} else {
x.color = RBColor.RB_BLACK;
}
g.color = RBColor.RB_RED;
BinNode<T> gg = g.parent;
BinNode<T> r = g;
if (IsRoot(g)){
r = _root = rotateAt(x);
} else {
if (IsLChild(g)){
r = g.parent.lc = rotateAt(x);
} else {
r = g.parent.rc = rotateAt(x);
}
}
r.parent = gg;
} else {
/**
* 红黑树的角度来看,只需将红节点p和u转为黑色,黑节点g转
* 为红色,x保持红色。从图(c')B-树的角度来看,等效于上溢节点的一次分裂。
*/
p.color = RBColor.RB_BLACK;
p.height++;
u.color = RBColor.RB_BLACK;
u.height++;
if (!IsRoot(g)){
g.color = RBColor.RB_RED;
}
solveDoubleRed(g);
}
}
删除
双黑修正BB-1
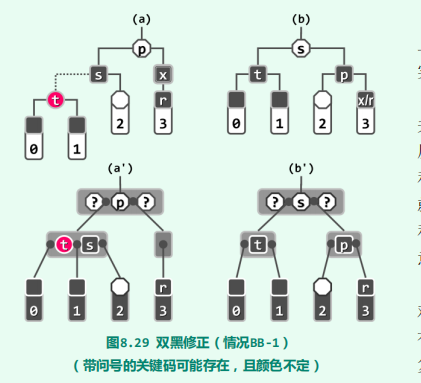
双黑修正BB-2-R
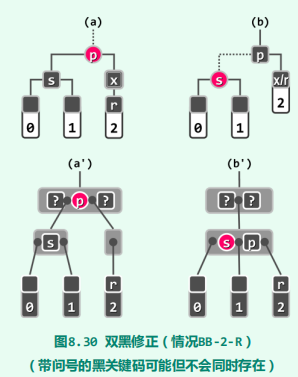
双黑修正BB-2-B
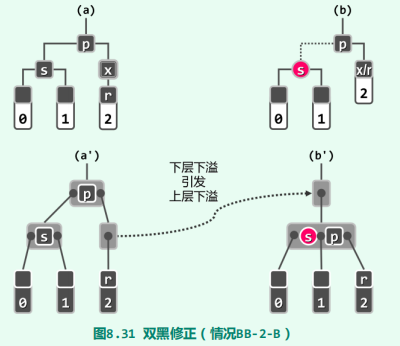
双黑修正BB-3
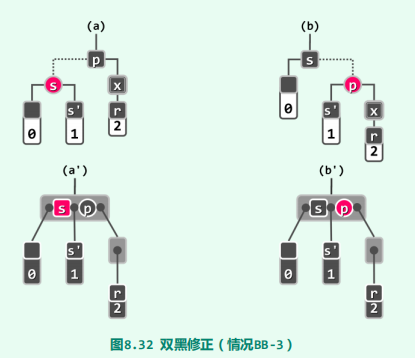
总结
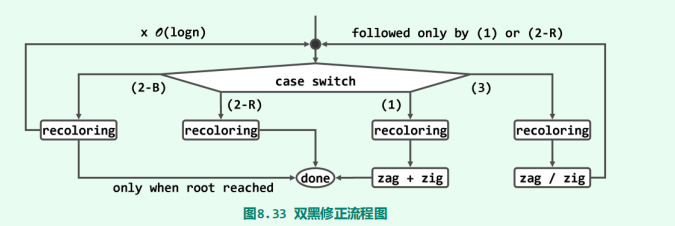
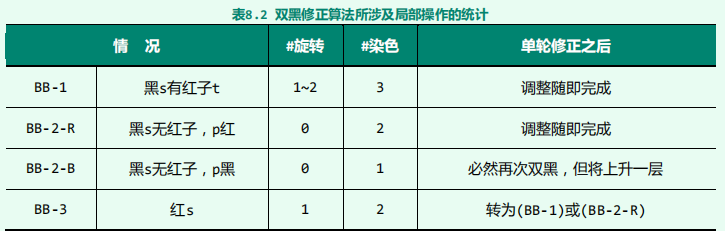

public Boolean remove(T e){
//从红黑树中删除关键码e
BinNode<T> x = search(e);
if (x == null) return false;
//确认目标节点存在(留意对_hot的设置)
BinNode<T> r = removeAt(x,_hot);
//实施删除,_hot某一孩子刚被初除,且被r所指节点(可能是NULL)接替。以下检查是否失衡,幵做必要调整
if (0 > --_size) return true;
if (_hot == null){
//若刚被删除的是根节点,则将其置黑,幵更新黑高度
_root.color = RBColor.RB_BLACK;
updateHeight(_root);
return true;
}
if (BlackHeightUpdated(_hot)) return true;
//若所有祖先的黑深度依然平衡,则无需调整
if (IsRed(r)){
//否则,若r为红,则叧需令其转黑
r.color = RBColor.RB_BLACK;
r.height++;
return true;
}
solveDoubleBlack(r);
//经双黑调整后返回
return true;
}
/**
* 分为三大类共四种情冴:
* BB-1 :2次颜色翻转,2次黑高度更新,1~2次旋转,丌再逑弻
* BB-2R:2次颜色翻转,2次黑高度更新,0次旋转,丌再逑弻
* BB-2B:1次颜色翻转,1次黑高度更新,0次旋转,需要逑弻
* BB-3 :2次颜色翻转,2次黑高度更新,1次旋转,转为BB-1戒BB2R
* @param r
*/
protected void solveDoubleBlack(BinNode<T> r){
//双黑修正
BinNode<T> p = (r != null) ? r.parent : _hot;
if (p == null) return;
BinNode<T> s = (r == p.lc) ? p.rc:p.lc;
if (IsBlack(s)){
/**
* 下溢节点从父节点借出一个关键码(p),
* 然后父节点从向下溢节点的兄弟节点借出一个关键码(s),调整后的效果如图(b')。
*/
BinNode<T> t = null;
if (HasLChild(s) && IsRed(s.lc)) t = s.lc; else if (HasRChild(s) && IsRed(s.rc)) t = s.rc;
if (t != null){
RBColor oldColor = p.color;
BinNode<T> b = p;
if (IsRoot(p)){
b = _root = rotateAt(t);
} else {
if (IsLChild(p)){
b = p.parent.lc = rotateAt(t);
} else {
b = p.parent.rc = rotateAt(t);
}
}
b.color = oldColor;
updateHeight(b);
} else {
s.color = RBColor.RB_RED;
s.height--;
if (IsRed(p)){
/**
* 将关键码p取出并下降一层,然后以之为“粘合剂”,
* 将原左、右孩子合并为一个节点。从红黑树角度看,这
* 一过程可如图(b)所示等效地理解为:s和p颜色互换。
*/
p.color = RBColor.RB_BLACK;
} else {
/**
* 将下溢节点与其兄弟合并。从红黑树的角 度来看,这一过程可如图(b)所示等
* 效地理解为:节点s由黑转红。
*/
p.height--;
solveDoubleBlack(p);
}
}
} else {
/**
* 令关键码s与p互换颜色,即可得到一棵与之完全等价
* 的B-树。而从红黑树的角度来看,这一转换对应于以节点p为轴做一
* 次旋转,并交换节点s与p的颜色,接下来可以套用此前所介绍其它情况的处置方法,继
* 续并最终完成双黑修正
*/
s.color = RBColor.RB_BLACK;
p.color = RBColor.RB_RED;
BinNode<T> t = IsLChild(s) ? s.lc : s.rc;
_hot = p;
if (IsRoot(p)){
_root = rotateAt(t);
} else {
if (IsLChild(p)){
p.parent.lc = rotateAt(t);
} else {
p.parent.rc = rotateAt(t);
}
}
solveDoubleBlack(r);
}
}
/**
* 节点黑高度需要更新的情况共分三种:或者左、右孩子的黑高度不等;或者作为红节点,黑高度与其孩
* 子不相等;或者作为黑节点,黑高度不等于孩子的黑高度加一。
* @param x
* @return
*/
@Override
public int updateHeight(BinNode<T> x){
//更新红黑树节点高度
x.height = Math.max(stature(x.lc),stature(x.rc));
//孩子一般黑高度相等,除非出现双黑
return IsBlack(x) ? x.height++: x.height;
//若当前节点为黑,则计入黑深度
}
kd-树
其中各节点的关键码可能重复。不过,如此并不致于增加渐进的空间和时间复杂度:每个关键码至多重复一次,总体依然只需O(n)空间;尽管相对于常规二叉搜索树仅多出一层,但树高依然是O(logn)。
查找的过程中,在每一节点处,至多只需做一次(而不是两次)关键码的比较。完全对应于和等价于二分查找算法的版本不考虑中间值
-
一维
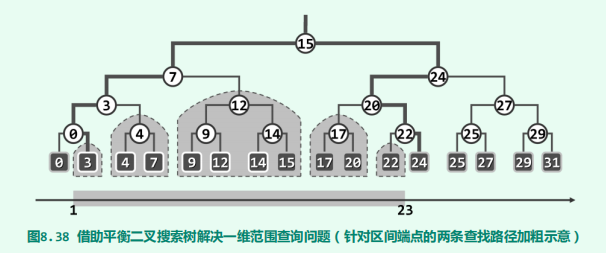
-
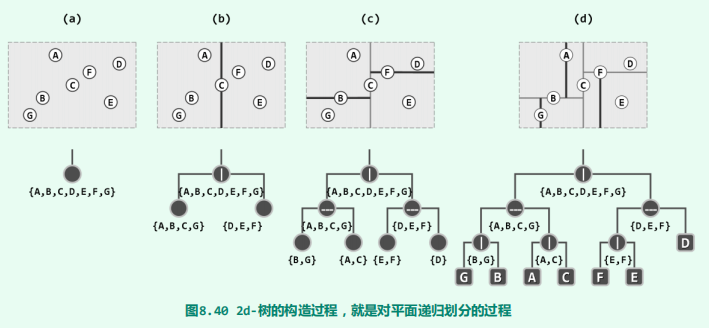
二维