队列
一、队列的基本概念
1、队列的定义
队列(queue)是只允许在一端进行插入操作,而在另一端进行删除操作的线性表。
队列是一种先进先出(First In First Out)的线性表,简称FIFO。允许插入的一端称为队尾,允许删除的一端称为队头。
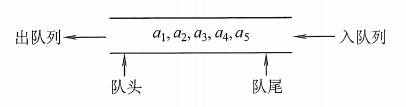
队头(Front):允许删除的一端,又称队首。
队尾(Rear):允许插入的一端。
空队列:不包含任何元素的空表。
2、队列的常见基本操作
InitQueue(&Q):初始化队列,构造一个空队列Q。
QueueEmpty(Q):判队列空,若队列Q为空返回true,否则返回false。
EnQueue(&Q, x):入队,若队列Q未满,将x加入,使之成为新的队尾。
DeQueue(&Q, &x):出队,若队列Q非空,删除队头元素,并用x返回。
GetHead(Q, &x):读队头元素,若队列Q非空,则将队头元素赋值给x。
二、队列的顺序存储结构
队列的顺序实现是指分配一块连续的存储单元存放队列中的元素,并附设两个指针:队头指针 front指向队头元素,队尾指针 rear 指向队尾元素的下一个位置。
1、顺序队列
队列的顺序存储类型可描述为:
1 #define MAXSIZE 50 //定义队列中元素的最大个数 2 typedef struct{ 3 ElemType data[MAXSIZE]; //存放队列元素 4 int front,rear; 5 }SqQueue;
初始状态(队空条件):Q->front == Q->rear == 0。
进队操作:队不满时,先送值到队尾元素,再将队尾指针加1。
出队操作:队不空时,先取队头元素值,再将队头指针加1。
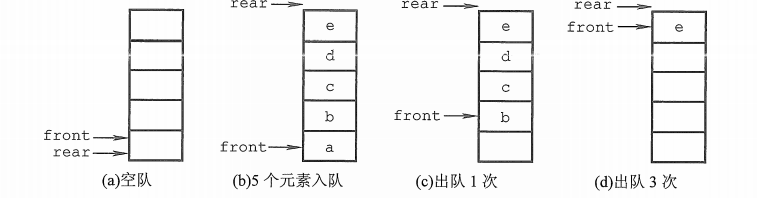
如图d,队列出现“上溢出”,然而却又不是真正的溢出,所以是一种“假溢出”。
2、循环队列
解决假溢出的方法就是后面满了,就再从头开始,也就是头尾相接的循环。我们把队列的这种头尾相接的顺序存储结构称为循环队列。
当队首指针Q->front = MAXSIZE-1后,再前进一个位置就自动到0,这可以利用除法取余运算(%)来实现。
初始时:Q->front = Q->rear=0。
队首指针进1:Q->front = (Q->front + 1) % MAXSIZE。
队尾指针进1:Q->rear = (Q->rear + 1) % MAXSIZE。
队列长度:(Q->rear - Q->front + MAXSIZE) % MAXSIZE。
出队入队时,指针都按照顺时针方向前进1,如下图所示:

那么,循环队列队空和队满的判断条件是什么呢?
显然,队空的条件是 Q->front == Q->rear 。若入队元素的速度快于出队元素的速度,则队尾指针很快就会赶上队首指针,如图( d1 )所示,此时可以看出队满时也有 Q ->front == Q -> rear
为了区分队空还是队满的情况,有三种处理方式:
(1)牺牲一个单元来区分队空和队满,入队时少用一个队列单元,这是种较为普遍的做法,约定以“队头指针在队尾指针的下一位置作为队满的标志”,如图 ( d2 )所示。
队满条件: (Q->rear + 1)%Maxsize == Q->front
队空条件仍: Q->front == Q->rear
队列中元素的个数: (Q->rear - Q ->front + Maxsize)% Maxsize
(2)类型中增设表示元素个数的数据成员。这样,队空的条件为 Q->size == O ;队满的条件为 Q->size == Maxsize 。这两种情况都有 Q->front == Q->rear
(3)类型中增设tag 数据成员,以区分是队满还是队空。tag 等于0时,若因删除导致 Q->front == Q->rear ,则为队空;tag 等于 1 时,若因插入导致 Q ->front == Q->rear ,则为队满。
我们重点讨论第一种方法
3、循环队列常见基本算法
(1)循环队列的顺序存储结构
1 typedef int ElemType; //ElemType的类型根据实际情况而定,这里假定为int 2 #define MAXSIZE 50 //定义元素的最大个数 3 /*循环队列的顺序存储结构*/ 4 typedef struct{ 5 ElemType data[MAXSIZE]; 6 int front; //头指针 7 int rear; //尾指针,若队列不空,指向队列尾元素的下一个位置 8 }SqQueue;
(2)循环队列的初始化
1 /*初始化一个空队列Q*/ 2 Status InitQueue(SqQueue *Q){ 3 Q->front = 0; 4 Q->rear = 0; 5 return OK; 6 }
(3)循环队列判队空
1 /*判队空*/ 2 bool isEmpty(SqQueue Q){ 3 if(Q.rear == Q.front){ 4 return true; 5 }else{ 6 return false; 7 } 8 }
(4)求循环队列长度
1 /*返回Q的元素个数,也就是队列的当前长度*/ 2 int QueueLength(SqQueue Q){ 3 return (Q.rear - Q.front + MAXSIZE) % MAXSIZE; 4 }
(5)循环队列入队
1 /*若队列未满,则插入元素e为Q新的队尾元素*/ 2 Status EnQueue(SqQueue *Q, ElemType e){ 3 if((Q->rear + 1) % MAXSIZE == Q->front){ 4 return ERROR; //队满 5 } 6 Q->data[Q->rear] = e; //将元素e赋值给队尾 7 Q->rear = (Q->rear + 1) % MAXSIZE; //rear指针向后移一位置,若到最后则转到数组头部 8 return OK; 9 }
(6)循环队列出队
1 /*若队列不空,则删除Q中队头元素,用e返回其值*/ 2 Status DeQueue(SqQueue *Q, ElemType *e){ 3 if(isEmpty(Q)){ 4 return REEOR; //队列空的判断 5 } 6 *e = Q->data[Q->front]; //将队头元素赋值给e 7 Q->front = (Q->front + 1) % MAXSIZE; //front指针向后移一位置,若到最后则转到数组头部 8 }
三、队列的链式存储结构
1、链队列
队列的链式存储结构表示为链队列,它实际上是一个同时带有队头指针和队尾指针的单链表,只不过它只能尾进头出而已。
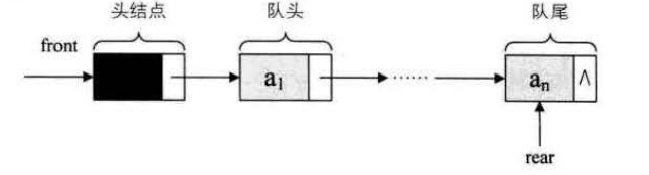
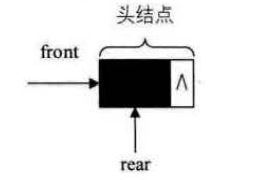
空队列时,front和real都指向头结点。
2、链队列常见基本算法
(1)链队列存储类型
1 /*链式队列结点*/ 2 typedef struct { 3 ElemType data; 4 struct LinkNode *next; 5 }LinkNode; 6 /*链式队列*/ 7 typedef struct{ 8 LinkNode *front, *rear; //队列的队头和队尾指针 9 }LinkQueue;
当 Q->front == NULL 并且 Q->rear == NULL 时,链队列为空。
(2)链队列初始化

1 void InitQueue(LinkQueue *Q){ 2 Q->front = Q->rear = (LinkNode)malloc(sizeof(LinkNode)); //建立头结点 3 Q->front->next = NULL; //初始为空 4 }
(3)链队列入队

1 Status EnQueue(LinkQueue *Q, ElemType e){ 2 LinkNode s = (LinkNode)malloc(sizeof(LinkNode)); 3 s->data = e; 4 s->next = NULL; 5 Q->rear->next = s; //把拥有元素e新结点s赋值给原队尾结点的后继 6 Q->rear = s; //把当前的s设置为新的队尾结点 7 return OK; 8 }
(4)链队列出队
出队操作时,就是头结点的后继结点出队,将头结点的后继改为它后面的结点,若链表除头结点外只剩一个元素时,则需将rear指向头结点。

1 /*若队列不空,删除Q的队头元素,用e返回其值,并返回OK,否则返回ERROR*/ 2 Status DeQueue(LinkQueue *Q, Elemtype *e){ 3 LinkNode p; 4 if(Q->front == Q->rear){ 5 return ERROR; 6 } 7 p = Q->front->next; //将欲删除的队头结点暂存给p 8 *e = p->data; //将欲删除的队头结点的值赋值给e 9 Q->front->next = p->next; //将原队头结点的后继赋值给头结点后继 10 //若删除的队头是队尾,则删除后将rear指向头结点 11 if(Q->rear == p){ 12 Q->rear = Q->front; 13 } 14 free(p); 15 return OK; 16 }
四、双端队列
1、定义
双端队列是指允许两端都可以进行入队和出队操作的队列,如下图所示。其元素的逻辑结构仍是线性结构。将队列的两端分别称为前端和后端,两端都可以入队和出队。

在双端队列进队时,前端进的元素排列在队列中后端进的元素的前面,后端进的元素排列在队列中前端进的元素的后面。在双端队列出队时,无论是前端还是后端出队,先出的元素排列在后出的元素的前面。
2、特殊的双端队列
在实际使用中,根据使用场景的不同,存在某些特殊的双端队列。
输出受限的双端队列:允许在一端进行插入和删除, 但在另一端只允许插入的双端队列称为输出受限的双端队列,如下图所示。

输入受限的双端队列:允许在一端进行插入和删除,但在另一端只允许删除的双端队列称为输入受限的双端队列,如下图所示。若限定双端队列从某个端点插入的元素只能从该端点删除,则该双端队列就蜕变为两个栈底相邻接的栈。



