HDU 4328 Cut the cake
Cut the cake
Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1250 Accepted Submission(s): 489
Problem Description:
Mark bought a huge cake, because his friend ray_sun’s birthday is coming. Mark is worried about how to divide the cake since it’s so huge and ray_sun is so strange. Ray_sun is a nut, you can never imagine how strange he was, is, and going to be. He does not eat rice, moves like a cat, sleeps during work and plays games when the rest of the world are sleeping……It is not a surprise when he has some special requirements for the cake. A considering guy as Mark is, he will never let ray_sun down. However, he does have trouble fulfilling ray_sun’s wish this time; could you please give him a hand by solving the following problem for him?
The cake can be divided into n*m blocks. Each block is colored either in blue or red. Ray_sun will only eat a piece (consisting of several blocks) with special shape and color. First, the shape of the piece should be a rectangle. Second, the color of blocks in the piece should be the same or red-and-blue crisscross. The so called ‘red-and-blue crisscross’ is demonstrated in the following picture. Could you please help Mark to find out the piece with maximum perimeter that satisfies ray_sun’s requirements?
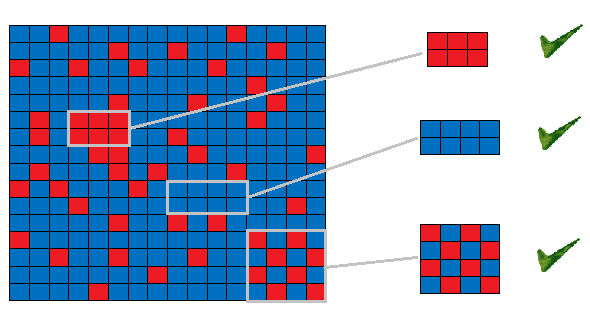
The cake can be divided into n*m blocks. Each block is colored either in blue or red. Ray_sun will only eat a piece (consisting of several blocks) with special shape and color. First, the shape of the piece should be a rectangle. Second, the color of blocks in the piece should be the same or red-and-blue crisscross. The so called ‘red-and-blue crisscross’ is demonstrated in the following picture. Could you please help Mark to find out the piece with maximum perimeter that satisfies ray_sun’s requirements?

Input
The first line contains a single integer T (T <= 20), the number of test cases.
For each case, there are two given integers, n, m, (1 <= n, m <= 1000) denoting the dimension of the cake. Following the two integers, there is a n*m matrix where character B stands for blue, R red.
For each case, there are two given integers, n, m, (1 <= n, m <= 1000) denoting the dimension of the cake. Following the two integers, there is a n*m matrix where character B stands for blue, R red.
Output
For each test case, output the cased number in a format stated below, followed by the maximum perimeter you can find.
Sample Input
2
1 1
B
3 3
BBR
RBB
BBB
Sample Output
Case #1: 4
Case #2: 8
Author
BJTU
Source
2012 Multi-University Training Contest 3
Recommend
zhoujiaqi2010 | We have carefully selected several similar problems for you: 4321 4366 4335 4377 4371
1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 using namespace std; 5 #include<algorithm> 6 #define N 1010 7 int n,m,h[N][N],l[N][N],r[N][N]; 8 char g[N][N]; 9 int ans=0,tmpl[N],tmpr[N]; 10 void solve(char key){ 11 memset(h,0,sizeof(h)); 12 memset(l,0,sizeof(l)); 13 memset(r,0,sizeof(r)); 14 int mx=0; 15 for(int i=1;i<=m;i++){ 16 l[0][i]=0;r[0][i]=m; 17 } 18 for(int i=1;i<=n;i++){ 19 int tmp=1; 20 for(int j=1;j<=m;j++){ 21 if(g[i][j]!=key)tmp=j+1; 22 else tmpl[j]=tmp; 23 } 24 tmp=m; 25 for(int j=m;j>=1;j--){ 26 if(g[i][j]!=key) tmp=j-1; 27 else tmpr[j]=tmp; 28 } 29 //记录好了一个点能到达的 最左边 和最右边, 30 //接下来就是dp了 31 for(int j=1;j<=m;j++){ 32 if(g[i][j]!=key){ 33 l[i][j]=1;h[i][j]=0;r[i][j]=m; 34 continue; 35 } 36 h[i][j]=h[i-1][j]+1; 37 l[i][j]=max(l[i-1][j],tmpl[j]); 38 r[i][j]=min(r[i-1][j],tmpr[j]); 39 mx=max(2*(r[i][j]-l[i][j]+1+h[i][j]),mx); 40 } 41 } 42 ans=max(ans,mx); 43 } 44 int main() 45 { 46 int T,tt=1;scanf("%d",&T); 47 for(int tz=1;tz<=T;tz++){ 48 ans=0; 49 scanf("%d%d",&n,&m); 50 for(int i=1;i<=n;i++) 51 scanf("%s",g[i]+1); 52 solve('B');solve('R'); 53 for(int i=1;i<=n;i++) 54 for(int j=1;j<=m;j++) 55 if((i+j)%2==0){ 56 if(g[i][j]=='B')g[i][j]='R'; 57 else g[i][j]='B'; 58 } 59 solve('B');solve('R'); 60 printf("Case #%d: ",tt++); 61 printf("%d\n",ans); 62 } 63 return 0; 64 }
思路:悬线法~~~~DP求满足题意的最大子矩阵的边长


