BZOJ_2813_奇妙的Fibonacci_线性筛
BZOJ_2813_奇妙的Fibonacci_线性筛
Description
Fibonacci数列是这样一个数列:
F1 = 1, F2 = 1, F3 = 2 . . .
Fi = Fi-1 + Fi-2 (当 i >= 3)
pty忽然对这个古老的数列产生了浓厚的兴趣,他想知道:对于某一个Fibonacci数Fi,
有多少个Fj能够整除Fi (i可以等于j),他还想知道所有j的平方之和是多少。
Input
第一行一个整数Q,表示Q个询问。
第二行四个整数:Q1, A, B, C
第i个询问Qi = (Qi-1 * A + B) mod C + 1(当i >= 2)
Output
Ai代表第i个询问有多少个Fj能够整除FQi。
Bi代表第i个询问所有j的平方之和。
输出包括两行:
第一行是所有的Ai之和。
第二行是所有的Bi之和。
由于答案过大,只需要输出除以1000000007得到的余数即可。
Sample Input
2
2 2 1 8
2 2 1 8
Sample Output
6
55
55
HINT
对于100%的数据保证:Q <= 3*10^6,C <= 10^7,A <= 10^7,B <= 10^7,1 <= Q1<= C
结论:(fn,fm)=f(n,m)
证明直接上图片:
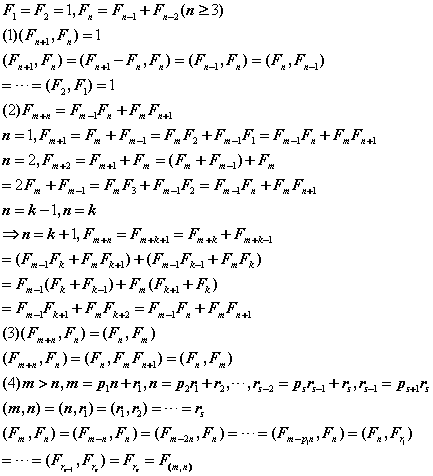
然后好办了。
fj|fi
(fi,fj)=fj
f(i,j)=fj
(i,j)=j 或 (i,j)=1且j=2。
线筛约数的平方之和,后面那个特判即可。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cstdlib>
#include <cmath>
using namespace std;
typedef long long ll;
#define mod 1000000007
#define N 10000050
#define M 10000000
int prime[N],cnt,cs[N],ys[N];
ll pf[N];
bool vis[N];
void init() {
ll i,j; ys[1]=pf[1]=1;
for(i=2;i<=M;i++) {
if(!vis[i]) {
prime[++cnt]=i,cs[i]=i,ys[i]=2,pf[i]=(ll(i)*i+1)%mod;
for(j=i*i;j<=M;j*=i) {
ys[j]=ys[j/i]+1;
pf[j]=(pf[j/i]+j*j)%mod;
}
}
for(j=1;j<=cnt&&i*prime[j]<=M;j++) {
int y=i*prime[j];
vis[y]=1;
if(i%prime[j]==0) {
cs[y]=cs[i]*prime[j];
if(i!=cs[i]) {
pf[y]=pf[i/cs[i]]*pf[prime[j]*cs[i]]%mod;
ys[y]=ys[i/cs[i]]*ys[prime[j]*cs[i]];
}
break;
}
cs[y]=prime[j];
pf[y]=pf[i]*pf[prime[j]]%mod;
ys[y]=ys[i]*ys[prime[j]];
}
}
}
int main() {
init();
ll Q,A,B,C;
int n;
ll ans1=0,ans2=0;
scanf("%d%lld%lld%lld%lld",&n,&Q,&A,&B,&C);
A%=C; B%=C;
while(n--) {
// printf("%d %lld\n",ys[Q],pf[Q]);
ans1+=ys[Q]+(Q&1); if(ans1>=mod) ans1-=mod;
ans2+=pf[Q]+(Q&1)*4; if(ans2>=mod) ans2-=mod;
Q=(Q*A+B)%C+1;
}
printf("%lld\n%lld\n",ans1,ans2);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号