POJ_1066_Treasure Hunt_判断线段相交
POJ_1066_Treasure Hunt_判断线段相交
Description
Archeologists from the Antiquities and Curios Museum (ACM) have flown to Egypt to examine the great pyramid of Key-Ops. Using state-of-the-art technology they are able to determine that the lower floor of the pyramid is constructed from a series of straightline walls, which intersect to form numerous enclosed chambers. Currently, no doors exist to allow access to any chamber. This state-of-the-art technology has also pinpointed the location of the treasure room. What these dedicated (and greedy) archeologists want to do is blast doors through the walls to get to the treasure room. However, to minimize the damage to the artwork in the intervening chambers (and stay under their government grant for dynamite) they want to blast through the minimum number of doors. For structural integrity purposes, doors should only be blasted at the midpoint of the wall of the room being entered. You are to write a program which determines this minimum number of doors.
An example is shown below:
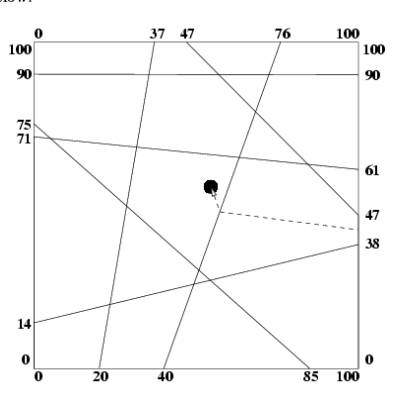
An example is shown below:

Input
The
input will consist of one case. The first line will be an integer n (0
<= n <= 30) specifying number of interior walls, followed by n
lines containing integer endpoints of each wall x1 y1 x2 y2 . The 4
enclosing walls of the pyramid have fixed endpoints at (0,0); (0,100);
(100,100) and (100,0) and are not included in the list of walls. The
interior walls always span from one exterior wall to another exterior
wall and are arranged such that no more than two walls intersect at any
point. You may assume that no two given walls coincide. After the
listing of the interior walls there will be one final line containing
the floating point coordinates of the treasure in the treasure room
(guaranteed not to lie on a wall).
Output
Print a single line listing the minimum number of doors which need to be created, in the format shown below.
Sample Input
7
20 0 37 100
40 0 76 100
85 0 0 75
100 90 0 90
0 71 100 61
0 14 100 38
100 47 47 100
54.5 55.4
Sample Output
Number of doors = 2
来自古文物和古玩博物馆(ACM)的考古学家已经飞到埃及去研究大金字塔的大金字塔。
利用最先进的技术,他们能够确定金字塔的底层是由一系列的直线墙构成的,这些墙与许多封闭的房间相交。目前,没有任何门可以进入任何一个房间。
这种最先进的技术也精确定位了宝藏室的位置。
这些专门的(和贪婪的)考古学家想要做的是把门从墙上炸开,到达宝藏室。然而,为了尽量减少在中间的房间里对艺术作品的损害(并在政府的资助下,他们想要通过最少的门数来进行爆炸)。
出于结构完整性的目的,门应该只在进入房间的墙壁的中点被炸开。你要写一个程序来确定这个最小的门数。
注意是进入房间的墙壁的中点而不是直线墙的中点。
那样这道题就变得非常简单了,直接枚举每个点判断这个点与宝藏的连线经过多少条线段即可。
然后+1就是答案。
代码:
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <queue>
#include <math.h>
using namespace std;
typedef double f2;
struct Point {
f2 x,y;
Point() {}
Point(f2 x_,f2 y_) :
x(x_),y(y_) {}
Point operator + (const Point &p) const {return Point(x+p.x,y+p.y);}
Point operator - (const Point &p) const {return Point(x-p.x,y-p.y);}
Point operator * (f2 rate) const {return Point(x*rate,y*rate);}
};
struct Line {
Point p,v;
Line() {}
Line(const Point &p_,const Point &v_) :
p(p_),v(v_) {}
};
f2 cross(const Point &p1,const Point &p2) {return p1.x*p2.y-p1.y*p2.x;}
f2 turn(const Point &p1,const Point &p2,const Point &p3) {
return cross(p3-p1,p2-p1);
}
bool judge(const Line &l1,const Line &l2) {
if(turn(l1.p,l1.v,l2.p)*turn(l1.p,l1.v,l2.v)>=0) return 0;
if(turn(l2.p,l2.v,l1.p)*turn(l2.p,l2.v,l1.v)>=0) return 0;
return 1;
}
Line a[50];
Point T;
int n;
int solve(const Line &l) {
int i,re=0;
for(i=1;i<=n;i++) {
if(judge(a[i],l)) re++;
}
return re;
}
int main() {
scanf("%d",&n);
if(!n) {
printf("Number of doors = %d",1); return 0;
}
int i;
int ans=1<<30;
for(i=1;i<=n;i++) {
scanf("%lf%lf%lf%lf",&a[i].p.x,&a[i].p.y,&a[i].v.x,&a[i].v.y);
}
scanf("%lf%lf",&T.x,&T.y);
for(i=1;i<=n;i++) {
Line l=Line(T,a[i].p);
ans=min(ans,solve(l));
l=Line(T,a[i].v);
ans=min(ans,solve(l));
}
printf("Number of doors = %d",ans+1);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号