Comet OJ - Contest #2简要题解

前言：

我没有小裙子，我太菜了。

A 因自过去而至的残响起舞

https://www.cometoj.com/contest/37/problem/A?problem_id=1528

容易发现那玩意增长的飞快，只要模拟就可以了

//❤ ayaponzu*
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cstdlib>
using namespace std;
typedef long long ll;
ll n;
ll f[100000];
int main() {
	int i;
	scanf("%lld",&n);
	f[1]=1,f[2]=1;
	ll sum=2;
	if(n==1) {puts("2"); return 0;}
	//if(n==2) {puts("2"); return 0;}
	for(i=3;i<=10000;i++) {
		f[i]=sum/2;
		sum+=f[i];
		if(sum>n) {
			printf("%d\n",i); return 0;
		}
	}
}

B 她的想法、他的战斗

https://www.cometoj.com/contest/37/problem/B?problem_id=1529

根据期望的线性性，可知\(E(q)=\frac{L+R}{2}\), 那么利润就是\(\frac{p-l}{r-l}(E(q)-p)\)
不难发现这东西是个二次函数，直接求最大值就可以了。
最优的\(p\)不在\([l,r]\)区间时需要特判。

//❤ ayaponzu*
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cstdlib>
using namespace std;
typedef long long ll;
typedef double f2;
ll n;
ll f[100000];
int main() {
	f2 l,r,L,R;
	scanf("%lf%lf%lf%lf",&l,&r,&L,&R);
	f2 q=(L+R)*0.5;
	f2 x=(q+l)/2;
	if(x<l) {
		puts("0.0000"); return 0;
	}
	f2 ans;
	if(x>r) {
		ans=q-r;
	}
	else ans=(-x*x+(q+l)*x-l*q)/(r-l);
	if(ans<1e-6) ans=0;
	printf("%.4f\n",ans);
}

C 言论的阴影里妄想初萌

https://www.cometoj.com/contest/37/problem/C?problem_id=1530

枚举有多少个点即可。

//❤ ayaponzu*
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cstdlib>
using namespace std;
typedef long long ll;
typedef double f2;
#define N 100050
#define mod 998244353
int n;
ll P,fac[N],inv[N];
ll qp(ll x,ll y=mod-2) {
	ll re=1; for(;y;y>>=1,x=x*x%mod) if(y&1) re=re*x%mod; return re;
}
ll C(int x,int y) {
	return fac[x]*inv[y]%mod*inv[x-y]%mod;
}
int main() {
	int i;
	ll x,y;
	scanf("%d%lld%lld",&n,&x,&y);
	P=x*qp(y)%mod;
	for(fac[0]=i=1;i<=n;i++) fac[i]=fac[i-1]*i%mod;
	inv[n]=qp(fac[n]);
	for(i=n-1;i>=0;i--) inv[i]=inv[i+1]*(i+1)%mod;
	ll ans=0;
	for(i=0;i<=n;i++) {
		ans=(ans+C(n,i)*qp(P,ll(i)*(i-1)/2))%mod;
	}
	printf("%lld\n",ans);
}

D 错综的光影所迷惑的思念是

https://www.cometoj.com/contest/37/problem/D?problem_id=1531

不难想到先枚举点集直径的中点\(x\)，那么限制就是距离\(x\)为\(\frac{i}{2}\)的点在不同的子树中至少要选出两个，其他小于\(i\)的可以随意选。
是一个类似\(2^{sz(x)}-1-\sum\limits_{t}(2^{sz(t)}-1)\)的一个式子。其中\(sz(t)\)表示以\(x\)为根，\(t\)的子树内有多少距离\(x\)为\(i\)的点。
有两个问题，一是点集直径中点可能卡在边上，二是\(i\)可能是奇数，我们在每条边上塞一个点就行了。

//❤ ayaponzu*
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cstdlib>
#include <queue>
using namespace std;
typedef long long ll;
#define mod 998244353
#define N 4050
int n,head[N],to[N<<1],nxt[N<<1],cnt;
ll mi[N],ans[N];
int siz[N],ssiz[N][N];
inline void add(int u,int v) {
	to[++cnt]=v; nxt[cnt]=head[u]; head[u]=cnt;
}
void dfs(int x,int y,int d,int t) {
	int i; 
	if(x<=n) {
		siz[d]++; ssiz[t][d]++;
	}
	for(i=head[x];i;i=nxt[i]) if(to[i]!=y) {
		dfs(to[i],x,d+1,t);
	}
}
int main() {
	scanf("%d",&n);
	int i,x,y,j;
	for(i=1;i<n;i++) scanf("%d%d",&x,&y),add(x,n+i),add(n+i,x),add(y,n+i),add(n+i,y);
	int ln=n+n-1;
	for(mi[0]=i=1;i<=ln;i++) mi[i]=(mi[i-1]<<1)%mod;
	for(x=1;x<=ln;x++) {
		int s=0,lst=0;
		memset(siz,0,sizeof(siz));
		if(x<=n) {
			siz[0]++; lst++;
		}
		for(i=head[x];i;i=nxt[i]) {
			s++;
			memset(ssiz[s],0,sizeof(ssiz[s]));
			dfs(to[i],x,1,s);
		}
		for(i=1;i<n;i++) {
			ll tmp=mi[siz[i]]-1;
			for(j=1;j<=s;j++) tmp=(tmp-(mi[ssiz[j][i]]-1))%mod;
			ans[i]=(ans[i]+tmp*mi[lst])%mod;
			lst+=siz[i];
		}
	}
	for(i=1;i<n;i++) printf("%lld\n",(ans[i]+mod)%mod);
}

E 情报强者追逐事件

https://www.cometoj.com/contest/37/problem/E?problem_id=1532

orz zsy

对于不在环上的那些，转移是可以直接合并的，按照拓扑序更新即可，转移类似\(f_x=f_x+(1-f_x)\times f_y\times s_y\)。
剩下的对于每个环来考虑，对于\(x\)，会被环上的任意一点\(y\)来更新到，如果在某一时刻环上相邻两个点\(u\)和\(v\)，且从\(u\)转移出来的概率是\(p\)，那么从\(v\)转移出去的概率就是\((1-f_v)\times s_u\times p+f_v\)，不难发现这是一个\(ax+b\)的形式，放到线段树上去维护就好了。

//❤ ayaponzu*
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cstdlib>
#include <queue>
using namespace std;
typedef long long ll;
#define mod 998244353
#define N 800050
char buf[100000],*p1,*p2;
int to[N],du[N],Q[N],n;
ll P[N],s[N],f[N];
#define nc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++)
int rd() {
	int x=0; char s=nc();
	while(s<'0'||s>'9') s=nc();
	while(s>='0'&&s<='9') x=(((x<<2)+x)<<1)+s-'0',s=nc();
	return x;
}
ll qp(ll x,ll y=mod-2) {
	ll re=1;for(;y;y>>=1,x=x*x%mod)if(y&1)re=re*x%mod; return re;
}
struct A {
	ll x,y;
	A() {x=y=0;}
	A(ll x_,ll y_) {x=x_,y=y_;}
	A operator + (const A &u) const {
		return A(x*u.x%mod, (y*u.x+u.y)%mod);
	}
}tr[N<<2];
#define ls p<<1
#define rs p<<1|1
int S[N],tp;
void build(int l,int r,int p) {
	if(l==r) {
		int x=l%tp;
		if(!x)x=tp;
		x=S[x];
		int y=(l-1)%tp;
		if(!y)y=tp;
		y=S[y];
		tr[p]=A((1-f[x])*s[y]%mod,f[x]);
		return ;
	}
	int mid=(l+r)>>1;
	build(l,mid,ls); build(mid+1,r,rs);
	tr[p]=tr[ls]+tr[rs];
}
A query(int l,int r,int x,int y,int p) {
	if(x<=l&&y>=r) return tr[p];
	int mid=(l+r)>>1;
	if(y<=mid) return query(l,mid,x,y,ls);
	else if(x>mid) return query(mid+1,r,x,y,rs);
	else return query(l,mid,x,y,ls)+query(mid+1,r,x,y,rs);
}
void dfs(int x) {
	if(!x||!du[x]) return ;
	S[++tp]=x;
	du[x]=0;
	dfs(to[x]);
}
int main() {
	n=rd();
	int i;
	ll x,y;
	for(i=1;i<=n;i++) {
		x=rd(),y=rd();
		P[i]=x*qp(y)%mod;
	}
	for(i=1;i<=n;i++) to[i]=rd();
	for(i=1;i<=n;i++) du[to[i]]++;
	for(i=1;i<=n;i++) f[i]=P[i];
	for(i=1;i<=n;i++) {
		x=rd(),y=rd();
		s[i]=x*qp(y)%mod;
	}
	int l=0,r=0;
	for(i=1;i<=n;i++) if(!du[i]) {
		Q[r++]=i;
	}
	while(l<r) {
		int x=Q[l++];
		du[to[x]]--;
		f[to[x]] = (f[to[x]]+(1-f[to[x]])*f[x]%mod*s[x])%mod;
		if(!du[to[x]]) {
			Q[r++]=to[x];
		}
	}
	//printf("%d\n",r);
	//for(i=0;i<n;i++) printf("%d\n",Q[i]);
	int j;
	for(i=1;i<=n;i++) {
		if(du[i]) {
			//puts("FUCK");
			tp=0;
			dfs(i);
			//puts("FUCK");
			build(1,tp<<1,1);
			//puts("FUCK");
			for(j=1;j<=tp;j++) f[S[j]]=query(1,tp<<1,j+1,tp+j,1).y;
			//printf("%d\n",tp);
		}
		f[i]=(f[i]%mod+mod)%mod;
		printf("%lld",f[i]);
		if(i!=n) printf(" ");
	}
}

F 真实无妄她们的人生之路

比赛时：

woc这个F我会啊，赶紧写赶紧写

woc我怎么写了两个小时还没过啊

woc终于过了，但是我没小裙子了...

https://www.cometoj.com/contest/37/problem/E?problem_id=1532

设\(w_i=\frac{P_i}{1-P_i}\)，表示选\(i\)产生的概率，最后答案再乘上\(\prod\limits_{i}(1-P_i)\)就可以了。
设\(f_j=[x^j](\prod\limits_{i=1}^{n}(w_ix+1))\)，也就是选\(j\)个的概率，这个可以分治\(ntt\)求出。
那么考虑删掉一个，假设删掉第\(i\)个，设退掉\(i\)之后的背包数组为\(g_j\)就是强制\(i\)不选，选\(j\)个的概率。
根据退背包那一套理论，可以得出\(g_j=f_j-g_{j-1}\times w_i\)
展开，可得\(g_j=\sum\limits_{k=0}^j(-1)^kw_i^kf_{j-k}\)
那么退掉第\(i\)个的答案\(ans_i=\sum\limits_{j=1}^na_j\sum\limits_{k=0}^j(-1)^kw_i^kf_{j-k}\)
\(ans_i=\sum\limits_{k=0}^n(-1)^kw_i^k\sum\limits_{j=k}^na_jf_{j-k}\)
设\(h_k=\sum\limits_{j=k}^na_jf_{j-k}\)，这是一个卷积形式。
那么\(ans_i=\sum\limits_{k=0}^n(-1)^kw_i^kh_k\)，多点求值即可。

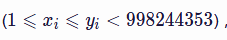
把概率为\(1\)的扔掉再把\(a\)数组平移若干位来求其他位置上的答案然后由于那些被扔掉的位置答案都相同所以用一开始的\(f\)和平移(若干位\(-1\))后的\(a\)数组求点积即可。
或者把上面的\(w_i\)改成\(\frac{1-P_i}{P_i}\)，orzzsy。

//❤ ayaponzu*
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cstdlib>
#include <queue>
using namespace std;
typedef long long ll;
#define mod 998244353
#define N 800050
char buf[100000],*p1,*p2;
#define nc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++)
int rd() {
	int x=0; char s=nc();
	while(s<'0'||s>'9') s=nc();
	while(s>='0'&&s<='9') x=(((x<<2)+x)<<1)+s-'0',s=nc();
	return x;
}
ll mem[N*60],*ptr=mem,fac[N],inv[N];
ll qp(ll x,ll y) {ll re=1;for(;y;y>>=1,x=x*x%mod)if(y&1)re=re*x%mod;return re;}
ll INV(ll x){return qp(x,mod-2);}
void ntt(ll *a,int len,int flg) {
	int i,j,k,t; ll tmp,w,wn;
	for(i=k=0;i<len;i++) {
		if(i>k) swap(a[i],a[k]);
		for(j=len>>1;(k^=j)<j;j>>=1) ;
	}
	for(k=2;k<=len;k<<=1) {
		t=k>>1; wn=qp(3,(mod-1)/k);
		if(flg==-1) wn=INV(wn);
		for(i=0;i<len;i+=k) {
			w=1;
			for(j=i;j<i+t;j++) {
				tmp=a[j+t]*w%mod;
				a[j+t]=(a[j]-tmp)%mod;
				a[j]=(a[j]+tmp)%mod;
				w=w*wn%mod;
			}
		}
	}if(flg==-1)for(tmp=INV(len),i=0;i<len;i++) a[i]=a[i]*tmp%mod;
}
ll A[N],B[N];
struct shion {
    ll *a;
	int len;
    shion() {}
    shion(int l) {len=l,a=ptr,ptr+=l;}
    void fix(int l) {len=l,a=ptr,ptr+=l;}
    void rev() {reverse(a,a+len);}
    void get_mod(int l) {int i;for(i=l;i<len;i++)a[i]=0;len=l;}
    void kuo(int l) {len=l,ptr=mem+len;}
	bool operator < (const shion &u) const {
		return len>u.len;
	}
    shion operator - (const shion &u) const {
        shion re(len);int i;
        for(i=0;i<len;i++) re.a[i]=(a[i]-u.a[i])%mod;
        return re;
    }
    shion operator + (const shion &u) const {
        shion re(max(len,u.len)); int i;
        for(i=0;i<re.len;i++) {
            re.a[i]=((i<len?a[i]:0)+(i<u.len?u.a[i]:0))%mod;
        }return re;
    }
    shion operator * (const shion &u) const {
        shion re(len+u.len-1);
        int i,l=1,j;
        if(re.len<=200) {
            for(i=0;i<len;i++)for(j=0;j<u.len;j++) {
                re.a[i+j]=(re.a[i+j]+ll(a[i])*u.a[j])%mod;
            }return re;
        }
        while(l<len+u.len)l<<=1;
        memset(A,0,sizeof(ll)*l);
        memset(B,0,sizeof(ll)*l);
        memcpy(A,a,sizeof(ll)*len);
        memcpy(B,u.a,sizeof(ll)*u.len);
        ntt(A,l,1),ntt(B,l,1);
        for(i=0;i<l;i++) A[i]=ll(A[i])*B[i]%mod;
        ntt(A,l,-1);
        for(i=0;i<re.len;i++) re.a[i]=A[i];
        return re;
    }
    void get_inv(const shion &u,int len) {
        if(len==1) {a[0]=INV(u.a[0]);return ;}
        get_inv(u,len>>1);
        int l=len<<1,i;
        memset(A,0,sizeof(ll)*l);
        memset(B,0,sizeof(ll)*l);
        memcpy(A,u.a,sizeof(ll)*min(u.len,len));
        memcpy(B,a,sizeof(ll)*len);
        ntt(A,l,1),ntt(B,l,1);
        for(i=0;i<l;i++) A[i]=B[i]*(2-ll(A[i])*B[i]%mod)%mod;
        ntt(A,l,-1);
        memcpy(a,A,sizeof(ll)*len);
    }
    shion Get_inv(int l) {
        shion re(l); re.get_inv(*this,l); return re;
    }
    shion operator / (shion u) {
        int n=len,m=u.len,l=1;
        while(l<(n-m+1))l<<=1;
        rev(),u.rev();
        shion v=u.Get_inv(l);
        v.get_mod(n-m+1);
        shion re=*this*v;
        rev(),u.rev();
        re.get_mod(n-m+1);
        re.rev();
        return re;
    }
    shion operator % (shion u) {
        shion re=*this-u*(*this/u); re.get_mod(u.len-1); return re;
    }
    shion Get_dao() {
        shion re(len-1);
        int i;
        for(i=1;i<len;i++) re.a[i-1]=ll(i)*a[i]%mod;
        return re;
    }
}fq[N<<2];
#define ls p<<1
#define rs p<<1|1
ll RE[N],qx[N];
void build(int l,int r,int p) {
    if(l==r) {
        fq[p].fix(2);
        fq[p].a[0]=-qx[l];
        fq[p].a[1]=1;
        return ;
    }
    int mid=(l+r)>>1;
    build(l,mid,ls),build(mid+1,r,rs);
    fq[p]=fq[ls]*fq[rs];
}
void get_val(shion F,int l,int r,int p,ll *re) {
    if(F.len<=450) {
        int i,j;
		ll t;
        for(i=l;i<=r;i++) {
            for(j=0,t=1;j<F.len;j++,t=ll(t)*qx[i]%mod) {
                re[i]=(re[i]+ll(t)*F.a[j])%mod;
            }
        }
        return ;
    }
    int mid=(l+r)>>1;
    get_val(F%fq[ls],l,mid,ls,re);
    get_val(F%fq[rs],mid+1,r,rs,re);
}
priority_queue<shion>q;
int n;
ll P[N],a[N],f[N],g[N],num[N],h[N],tmpa[N];
void geth() {
	shion ta(n+1),tb(n+1);
	int i;
	for(i=0;i<=n;i++) ta.a[i]=a[n-i];
	for(i=0;i<=n;i++) tb.a[i]=f[i];
	shion tc=ta*tb;
	for(i=0;i<=n;i++) h[i]=tc.a[n-i];
}
int is[N],to[N];
int main() {

	n=rd();

	int i,tot=0,ln=n;
	ll x,y;
	for(i=0;i<n;i++) a[i]=rd();
	for(i=1;i<=ln;i++) {
		x=rd(),y=rd();
		P[i]=x*INV(y)%mod;
		num[i]=INV(1-P[i]);
		if(P[i]==1) {
			is[i]=1;
		}else {
			P[++tot]=P[i];
			num[tot]=num[i];
			to[i]=tot;
		}
	}
	if(!tot) {
		for(i=1;i<=n;i++) {
			printf("%lld",a[ln-1]);
			if(i!=n) printf(" ");
		}
		return 0;
	}
	memcpy(tmpa,a,sizeof(a));
	for(i=0;i<=n;i++) a[i]=a[i+ln-tot];
	n=tot;
	for(i=1;i<=n;i++) {
		shion t(2);
		t.a[0]=1,t.a[1]=P[i]*num[i]%mod;
		q.push(t);
	}
	for(i=1;i<n;i++) {
		shion aa=q.top(); q.pop();
		shion bb=q.top(); q.pop();
		q.push(aa*bb);
	}

	ll tmp=1;
	for(i=1;i<=n;i++) tmp=tmp*(1-P[i])%mod;
	shion qwq=q.top();
	for(i=0;i<=n;i++) f[i]=qwq.a[i];
	geth();
	
	
	for(i=1;i<=n;i++) qx[i]=P[i]*num[i]%mod;
	build(1,n,1);
	shion ff(n+1);
	for(i=0;i<=n;i++) {
		if(i&1) ff.a[i]=mod-h[i];
		else ff.a[i]=h[i];
	}
	get_val(ff,1,n,1,RE);

	if(tot!=ln) for(i=0;i<=n;i++) a[i]=tmpa[i+ln-tot-1];
	ll OTH=0;
	for(i=0;i<=n;i++) {
		//printf("%lld\n",a[i]);
		OTH=(OTH+a[i]*f[i])%mod;
	}
	OTH=(OTH*tmp%mod+mod)%mod;

	for(i=1;i<=ln;i++) {
		if(is[i]) {
			printf("%lld",OTH);
		}else {
			ll ans=RE[to[i]]*num[to[i]]%mod*tmp%mod;
			printf("%lld",(ans+mod)%mod);
		}
		if(i!=ln) printf(" ");
	}
}

posted @ 2019-04-27 10:54 fcwww 阅读(710) 评论(0) 编辑收藏举报

刷新页面返回顶部

fcwww

一杯茶，一包烟，一个破题调一天

Comet OJ - Contest #2简要题解

Comet OJ - Contest #2简要题解

前言：

A 因自过去而至的残响起舞

B 她的想法、他的战斗

C 言论的阴影里妄想初萌

D 错综的光影所迷惑的思念是

E 情报强者追逐事件

F 真实无妄她们的人生之路

公告