排序即把无序的序列排成有序
排序稳定性指待排序列有两个或两个以上的相同关键字时,他们排序前后的相对顺序不变即为稳定,否则为不稳定
排序算法分类:
1、插入类:在一个已经有序的序列中,插入一个新的关键字
例如:直接插入排序、折半插入排序、希尔排序
2、交换类:每一趟排序,通过一系列交换动作,让一个关键字排到最终位置
例如:冒泡排序、快速排序
3、选择类:每一趟排序选出最小或最大的关键字,把他和序列第一个或最后一个关键字交换
例如:简单选择排序、堆排序
4、归并类:将两个或两个以上的有序序列合并成一个新的有序序列
例如:二路归并
5、基数类:基于多关键字思想,例如把扑克牌先按花色再按大小排序
——————————————————————————————————————————
插入类排序
直接插入排序
每趟直接将待排序关键字按照值大小插入到已经排号的序列中
代码:
void InsertSort(int R[],int n)
{
int i,j;
int temp;
for(i=1;i<n;i++)
{
temp=R[i];//待插入关键字暂存temp
j=i-1;
while(j>=0&&temp<R[j])//找位置
{
R[j+1]=R[j];
--j;
}
R[j+1]=temp;//插入
}
}
时间复杂度为O(n^2),空间复杂度为O(1)
折半插入排序
与直接插入排序的区别在于查找插入位置的方法不同
例子:
现有序列:13,38,49,65,76,97 待插入关键字:27,49
1、low=0,high=5,m=(0+5)/2=2(向下取整),下标为2的关键字是49, 27<49,high=m-1=1
2、low=0,high=1,m=(0+1)/2=0,下标为0的关键字是13,27>13,low=m+1=1
3、low=high=1,m=(1+1)/2=1,下标为1的关键字是38,27<38 ,high=m-1=0
因为high<low 折半查找结束,27应该插入在high索引关键字之后 即插入后序列为 13 27 38 49 65 76 97 待插入 49
折半查找时间复杂度为O(n^2) 空间复杂度为O(1)
希尔排序
又称为缩小增量排序,将待排序列分为几个子序列,分别对这几个子序列进行直接插入排序
例子:
原始序列:49 38 65 97 76 13 27 49 55 04
1、以增量5分割序列,得到以下子序列
序列1:49 13
序列2: 38 27
序列3: 65 49
序列4: 97 55
序列5: 76 04
对以上5个子序列分别进行直接插入排序,结果如下
13 49
27 38
49 65
55 97
04 76
整体为13 27 49 55 04 49 38 65 97 76
在分别以增量3和增量1来分割再排序
序列1:13 55 38 76
序列2: 27 04 65
序列3: 49 49 97
整体为13 04 49 38 27 49 55 65 97 76
增量为1的过程省略
希尔排序时间复杂度与增量选取有关,是不稳定的排序算法(相同关键字相对位置可能变化)
增量序列的最后一个值一定取1
增量序列的值尽量没有除1之外的公因子
希尔排序空间复杂度为O(1)
——————————————————————————————————————————
交换类排序
起泡排序又称冒泡排序,小的关键字像气泡一样逐渐向上移动
起泡排序算法结束的条件是在一趟排序过程中没有发生关键字交换
void BubbleSort(int R[],int n)
{
int i,j,flag=0;
int temp for(i=n-1;i>=1;--i)
{
flag=0;//记录本次是否发生交换
for(j=1;j<=i;++j)
{
if(R[j-1]>R[j])
{
temp=R[j];
R[j]=R[i];
R[i]=temp;
flag=1;
}
}
if(flag==0)
{
return;
}
}
}
冒泡排序时间复杂度为O(n^2),空间复杂度为O(1)
快速排序
每一趟为当前所有子序列各选一个关键字作为枢轴,将序列中比枢轴小的移到前边,大的移到后边。
例子:
原始序列:49 38 65 97 76 13 27 49
i j
第一趟快速排序,以第一个数49为枢轴,j从后向前扫描,直到遇见比枢轴小的数
49 38 65 97 76 13 27 49
i j
将27交换到i的位置上(不用担心数值覆盖丢失问题,枢轴的值已提前保存)
27 38 65 97 76 13 空 49
i j
使用i 变换扫描方向,从前向后扫描 直到遇见比枢轴大的数65 i停止
27 38 65 97 76 13 空 49
i j
将65交换到j的位置上
27 38 空 97 76 13 65 49
i j
接着使用j继续........直到i与j重合 将枢轴的关键字放在重合位置上 第一趟快速排序完成 枢轴位置上的关键字到达最终位置
下一趟将以上一趟的枢轴为边界将序列划分为两个更小的序列
两个序列同时开始快速排序......
代码:
void QuickSort(int R[],int low,int high)
{
int temp;
int i=low,j=high;
if(low<high)
{
temp=R[low];
while(i<j)
{
while(j>i&&R[j]>=temp)
{
--j;//从右往左扫描 找到一个小于temp的关键字
}
if(i<j)
{
R[i]=R[j];
++i;
}
while(i<j&&R[i]>=temp)//从左往右扫描,找到一个大于temp的关键字
{
++i;
}
if(i<j)
{
R[j]=R[i];
--j;
}
}
R[i]=temp;
QuickSort(R,low,i-1);//temp左面递归处理
QuickSort(R,i+1,high); //temp右面递归处理
}
}
快速排序时间复杂度为O(nlogn),空间复杂度为O(logn)
——————————————————————————————————————————
选择类排序
简单选择排序:从头到尾扫描序列,找出最小的一个关键字,和第一个关键字交换
代码:
void SelectSort(int R[],int n)
{
int i,j,k;
int temp;
for(int i=0;i<n;i++)
{
k=i;
for(j=i+1;j<n;j++)//从无序序列中挑选出最小关键字
{
if(R[k]>R[j])
{
k=j;
}
}
temp=R[i];
R[i]=R[k];
R[k]=temp;
}
}
简单选择排序时间复杂度为O(n^2),空间复杂度为O(1)
堆排序
可以把堆看成一颗完全二叉树,且满足任何一个非叶结点的值都不大于(或不小于)其左右孩子结点的值。
若父亲大孩子小,则这样的堆叫做大顶堆;若父亲小孩子大,则这样的堆叫做小顶堆。
执行过程例子:
原始序列:49 38 65 97 76 13 27 49
建堆:先将序列调整为一个大顶堆
76 13 27 49 是叶子结点 没有左右孩子满足堆的定义
从97开始,按 97 65 38 49的顺序依次调整
97>49满足定义不需要调整
65>13,65>27满足定义
38<97,38<76,不满足定义和孩子中大的交换,38和97交换,但38<49,38和49交换
49<97,49<65,49和97交换,49<76 继续交换
此时已建立好大顶堆,序列为97 76 65 49 49 13 27 38,将堆顶关键字97与最后一个关键字38交换,第一趟排序完成。
97到达最终位置 对除97以外的序列重新调整为大顶堆即可。

代码:
void Sift(int R[],int low,int high)
{
int i=low,j=2*i;
int temp=R[i];
while(j<=high)
{
if(j<high&&R[j]<R[j+1]){//若右孩子较大 则把j指向右孩子
++j;
}
if(temp<R[j]){
R[i]=R[j];//继续向下调整
i=j;
j=2*i;
}
else{
break;
}
}
R[i]=temp; //被调整结点放入最终位置
}
void heapSort(int R[],int n)
{
int i;
int temp;
for(i=n/2;i>=1;--i)
{
Sift(R,i,n);//建立初始堆
}
for(i=n;i>=2;--i)
{
temp=R[1];//以下三句 换出根节点 放入最终位置
R[1]=R[i];
R[i]=temp;
Sift(R,1,i-1); //在减少一个关键字的序列中进行调整
}
}
堆排序时间复杂度为O(nlogn)(最坏情况下也是),空间复杂度为O(1),堆排序适用关键字很多的情况 比如从10000个关键字中找10个最小的
——————————————————————————————————————————————————————————————
二路归并排序
过程:
1、将原始序列看成n个只含有一个关键字的子序列
2、两两归并
3、归并后的有序二元组子序列继续归并
4、最后归并成一个序列
二路归并排序时间复杂度为O(nlogn)空间复杂度为O(n)
——————————————————————————————————————————————————————————
基数排序
第一种实现方式是最高位优先,先按最高位排成若干子序列,再对每个子序列按次高位排序。例如对扑克牌先按花色再按大小排序。
第二种是实现方式是最低位优先,每次排序所有关键字参与,例子如下:
原始序列: 247 109 547 024
因为数字的范围是0~9,准备十个队列存放关键字(如果是英语单词就是26个队列)
1、按最低位排序结果如下
队列4:024
队列9:109
队列7:247、547
其他队列为空
按0到9的顺序对队列进行收集 结果为024、247、547、109
2、按次低位进行排序
队列0:109
队列2:024
队列4:247、547
其他队列为空
按0到9的顺序对队列进行收集 结果为109、024、247、547
3、按首位进行排序
队列0:024
队列1:109
队列2:247
队列5:547
其他队列为空
按0到9的顺序对队列进行收集 结果为:024、109、247、547
基数排序的时间复杂度为O(d(n+rd)),空间复杂度为O(rd)
n为序列的关键字数,d为关键字位数,rd为关键字基的个数(比如数字为10,字母为26)
————————————————————————————————————————————————————
外部排序:将内存作为工作空间来辅助外存数据的排序
外部排序常用归并排序
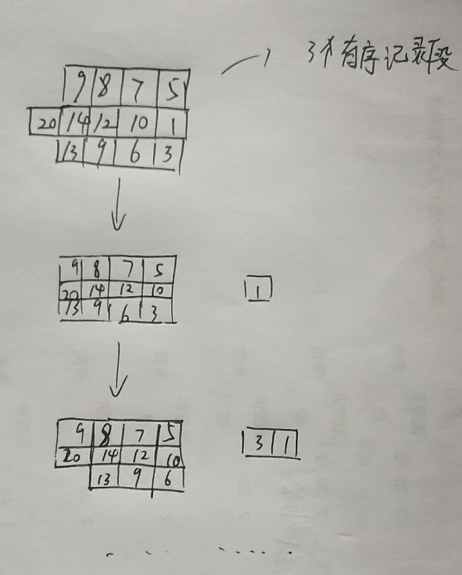
重要子算法:
置换-选择算法:用于产生上边的m个有序记录段

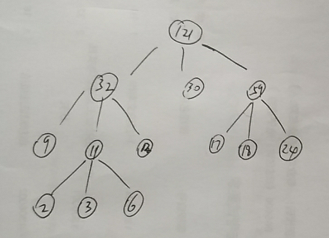
最佳归并树:将当前m组(每组k个有序记录段)记录归并成m个有序记录段的过程称为一趟归并,为了使得归并次数少,需要使用最佳归并树
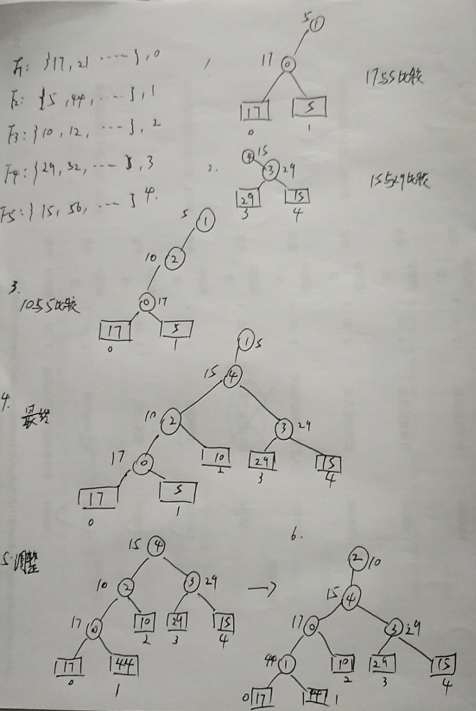
败者树:归并排序中需要从当前k个值选出最值,使用败者树可提高效率
——————————————————————————————————————————————————————————
排序小结:
1、时间复杂度
平均情况下(快些归队),快速排序,希尔排序,归并排序、堆排序均为O(nlogn),其他均为O(n^2),基数排序为O(d(n+rd))
最坏情况下,快速排序为O(n^2),其他与平均情况下相同
2、空间复杂度
快速排序O(logn),归并排序O(n),基数排序O(rd),其他皆是O(1)
3、稳定性
(快些选堆)快速排序、希尔排序、简单选择排序、堆排序都是不稳定的排序算法
4、其他
1、经过一趟排序能够保证一个关键字到达最终位置,这样的排序是交换类的两种(冒泡、快速)和选择类的两种(简单选择、堆)
2、排序算法的关键字比较次数和原始序列无关——简单选择排序和折半插入排序
3、排序算法的排序趟数和原始序列有关——交换类排序



