图由结点的有穷集合V和边集合E组成
有向图与无向图
入度与出度
有向完全图与无向完全图:前者具有n*(n-1)条边,后者具有n*(n-1)/2条边
简单路径:顶点不重复出现
连通图:无向图中,任意两个顶点都连通的图即为连通图。否则,图中的极大联通子图称为连通分量。
强连通图与强连通分量:针对于有向图
————————————————————————————————
邻接矩阵:图的顺序存储结构,1为有边,0为无边
对于无向图 图的邻接矩阵是对称的
矩阵中第i行的元素之和即为顶点i的出度,第j列的元素之和为顶点j的入度
结构型定义:
typedef struct
{
int no;//顶点编号
char info;//其他信息 可省略
} VertexType;//结点类型
typedef struct
{
int edges[maxSize][maxSize];//有权图则将int改为float
int n,e;//顶点数与边数
VertexType vex[maxSize];
}MGraph;
——————————————————————————————————————
邻接表:图的链式存储结构
领接表由单链表的表头形成顶点表和单链表其余结点形成的边表两部分组成
结构型定义
typedef struct ArcNode
{
int adjvex;//边所指向的结点
struct ArcNode *nextarc;//下一条边的指针
int info;//权值可省略
}ArcNode;
typedef struct
{
char data;//顶点信息
ArcNode *firstarc;//第一条边的指针
}VNode;
typedef struct
{
VNode adjlist[maxsize];//邻接表
int n,e;//订单数以及边数
}AGraph;
_______________________________________________________
邻接多重表
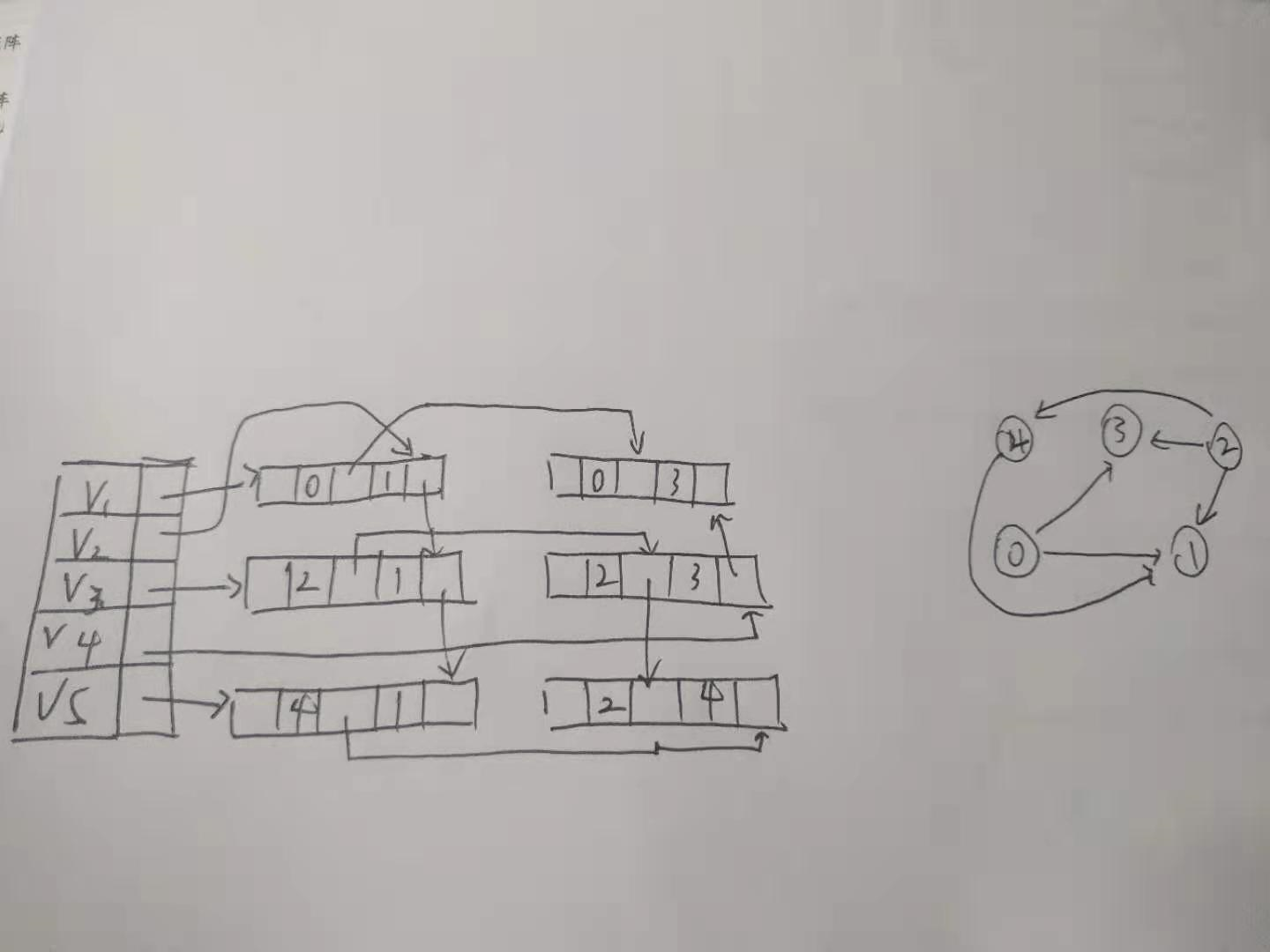
————————————————————————————————————————————————
深度优先遍历DFS(邻接表)类似于二叉树的先序遍历
int visit[maxsize];//初始所有元素为0,表示所有顶点未被访问
void DFS(AGraph *G,int v)
{
ArcNode *p;
visit[v]=1;
Visit(v);//访问顶点
p=G->adjlist[v].firstarc;
while(p!=NULL)
{
if(visit[p->adjvex]==0)//顶点未被访问,则递归访问顶点
{
DFS(G,p->adjvex);
p=p->nextarc;//下一条边
}
}
}
把图的深度优先遍历过程所经过的边保留,其余边删掉。会形成深度优先搜索树。
广度优先遍历BFS 类似于树的层次遍历
void BFS(AGraph *G,int v,int visit[maxszie])
{
ArcNode *p;
int que[maxSize],front=0,rear=0;//队列定义简单写法
int j;
Visit(v);
visit[v]=1;
rear=(rear+1)%maxSize;
que[rear]=v;//当前顶点v进队
while(front!=rear)//队空时说明遍历完成
{
front=(front+1)%maxSize;//顶点出队
j=que[front];
p=G->adjlist[j].firstarc;//p指向出队顶点j的第一条边
while(p!=NULL)//将p所有的邻接点中未被访问的入队
{
if(visit[p->adjvex]==0)//当前顶点未被访问
{
Visit(p->adjvex);
visit[p->adjvex]=1;
rear=(rear+1)%maxSize;
que[rear]=p->adjvex; //顶点进队
}
p=p->nextarc;//p指向下一条边
}
}
}
____________________________________________________
最小生成树
普利姆算法
执行过程:从树中某一个顶点vo开始,
将vo到其他顶点的所有边当作侯选边
重复以下步骤n-1次,使得剩余n-1个顶点并入生成树中
1、从侯选边中挑选出权值最小的边输出,将与该边另一端相接的顶点v并入生成树
2、考察所有剩余顶点vi,如果(v,vi)的权值比lowcost[vi]小,则用(v,vi)的权值更新lowcost[vi]
代码如下:
void Prim(MGraph g,int vo,int &sum)
{
int lowcost[maxsize],vset[maxsize],v;
int i,j,k,min;
v=vo;
for(i=0;i<g.n;++i)
{
lowcost[i]=g.edges[vo][i];
vset[i]=0;
}
vset[vo]=1;//将vo并入树中
sum=0;//sum清零 用来累计树的·权值
for(i=0;i<g.n-1;++i)
{
min=INF;//INF是一个已经定义的比图中所有边权值都大的常量
for(j=0;j<g.n;++j)//循环选出侯选边最小者
{
if(vset[j]==0&&lowcost[j]<min)
{
min=lowcost[j];
k=j;
}
}
vset[k]=1;
v=k;
sum+=min;//sum记录最小生成树权值
for(j=0;j<g.n;++j)//以刚并入的顶点v为媒介更新侯选边
{
if(vset[j]==0&&g.edges[v][j]<lowcost[j])
lowcost[j]=g.edges[v][j];
}
}
}
普利姆算法时间复杂度只与图中顶点有关系,与边数没有关系,因此普利姆算法适用于稠密图
克鲁斯卡尔算法:每次找出候选边中权值最小的边,不构成回路则并入生成树(手工构造生成树常用方法)
克鲁斯卡尔算法的时间复杂度主要由边数e决定,与顶点无关,适用于稀疏图
普利姆算法与克鲁斯卡尔算法都是针对于无向图的
_______________________________________________________________________________
最短路径
迪杰斯特拉算法:求图中某一顶点到其余各顶点的最短路径
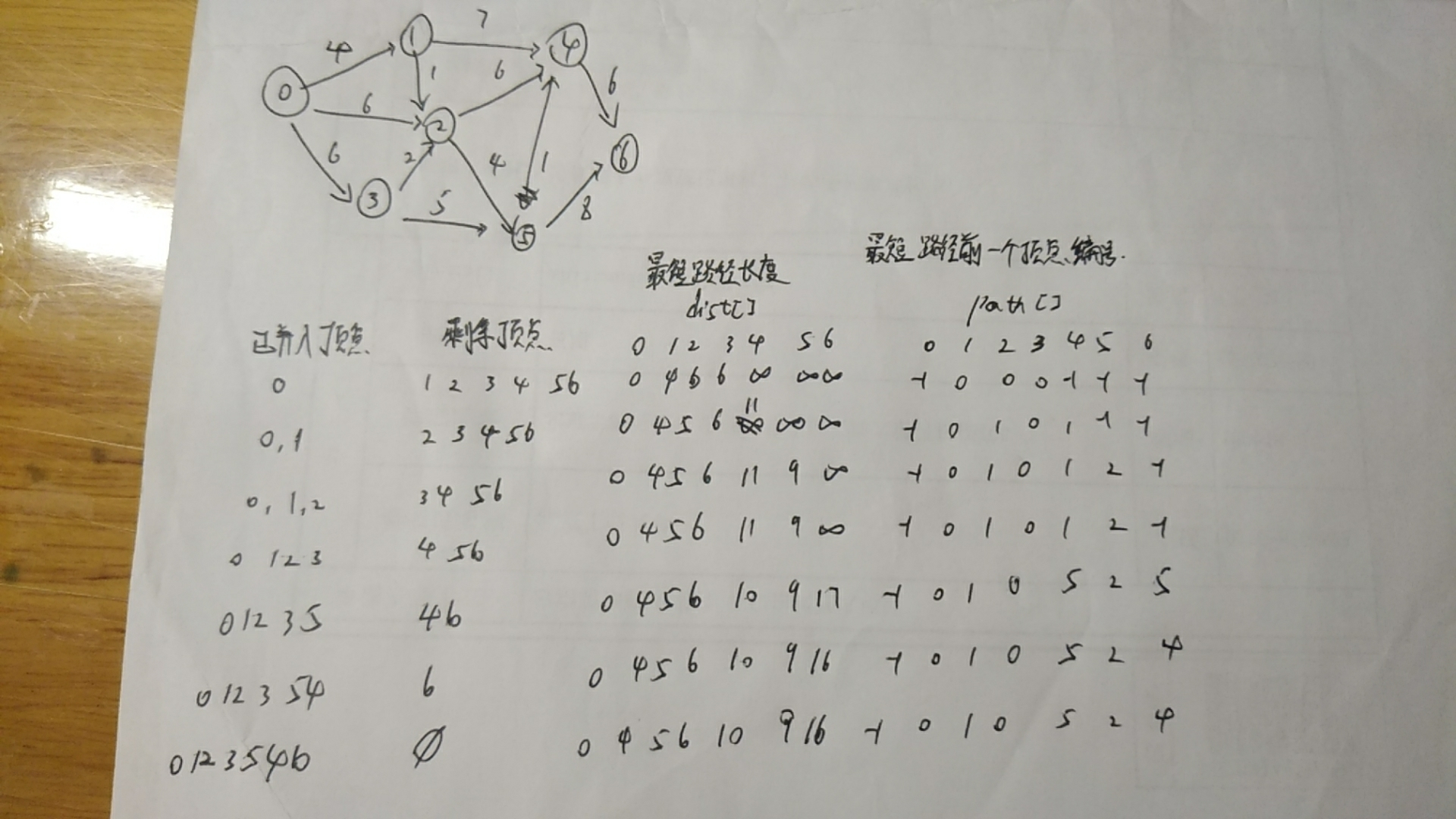
弗洛伊德算法:求图中任意一对顶点间的最短路径
初始时设置两个矩阵A和Path A用来记录当前已经求得的任意两个点最短路径,Path用来记录最短路径中间结点
执行过程:
1、初始化矩阵A为图邻接矩阵,将矩阵Path的元素全部设置为-1
2、以顶点k为中间结点,k取0~n-1,对图中所有顶点对进行如下检测与修改
3、如果A[i][j]>A[i][k]+A[k][j] 则将A[i][j]改为A[i][k]+A[k][j]的值,将P[i][j]改为k
void Floyd(MGraph g,int Path[][maxSize])
{
int i,j,k;
int A[maxsize][maxsize];
fot(i=0;i<g.n;i++)
{
for(j=0;j<g.n;j++)
{
A[i][j]=g.edges[i][j];
Path[i][j]=-1;
}
}
for(k=0;k<g.n;k++)
{
for(i=0;i<g.n;i++)
{
for(j=0;j<g.n;j++)
{
if(A[i][j]>A[i][k]+A[k][j])
{
A[i][j]=A[i][k]+A[k][j];
Path[i][j]=k;
}
}
}
}
}
__________________________________________________________
拓扑排序:对一个有向无环图进行拓扑排序,是将G中所有顶点排成一个线性序列(不唯一)
AOV网,以顶点表示活动的有向图
排序过程:
1、从有向图中选择一个没有前驱的顶点输出
2、删除1中顶点,并且删除从该顶点发出的全部边
3、重复上述两步,直至图中不存在没有前驱的结点
需要修改邻接表表头结构定义
typedef struct
{
char data;
int count;//结点的入度
ArcNode *firstarc;
}VNode;
int TopSort(AGraph *G)
{
int i,j,n=0;
int stack[maxSize],top=-1;//初始化栈
ArcNode *p;
for(i=0;i<G->n;++i)//图中顶点从0开始编号
{
if(G->adjlist[i].count==0)
{
stack[++top]=i;
}
}
while(top!=-1)
{
i=stack[top--];//顶点出栈
++n;
cout<<i<<" ";//输出顶点
p=G->adjlist[i].firstarc;
while(p!=NULL)//所有由此顶点引出的边所指向的顶点入度减少1,入度变为0的入栈
{
j=p->adjvex;
--(G->adjlist[j].count);
if(G->adjlist[j].count==0)
{
stack[++top]=j;
}
p=p->nextarc;
}
}
if(n==G->n)
return 1;
else
return 0;
}
AOE网:活动在边上的网
与aov网相同点:都是有向无环图
与aov网不同点:aoe网边表示活动,边有权值,边代表活动持续时间
关键路径是图中的最长路径,也是整个工期所完成的最短时间
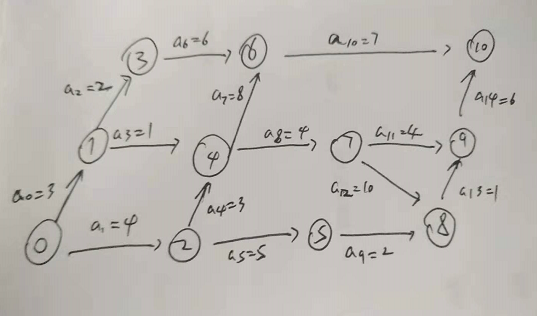
求关键路径过程
1、求ve(k),为顶点k代表的事件最早发生时间
1.1先求图的拓扑排序 ,例为0,1,2,3,4,5,6,7,8,9,10
1.2按顺序求事件最早发生时间
ve0=0、ve1=3、ve2=4
ve3=5、ve4=max(ve1+a3,ve2+a4)=7、ve5=9、
ve6=15、ve7=11、ve8=21
ve9=22、ve10=28
2、求vl(k),为事件k的最迟发生时间,是在不推迟整个工期的条件下,该事件deadline
2.1求图的逆拓扑排序,例为10,9,6,8,5,7,3,4,1,2,0
2.2按顺序求事件最迟发生时间
vl10=28、vl9=22、vl6=21
vl8=21、vl5=19、vl7=min(vl9-a11,vl8-a12)=11
vl3=15、vl4=7、vl1=6
vl2=4、vl0=0
3下面来求每个活动ak的最早和最迟发生时间分别于eak和lak表示,事件代表新活动的开始或者旧活动的结束
3.1求最早发生时间
ea0=ea1=ve0=0、ea2=ea3=ve1=3
ea4=ea5=ve2=4、ea6=ve3=5
ea7=ea8=ve4=7、ea9=ve5=9、ea10=ve6=15
ea11=ea12=ve7=11、ea13=ve8=21、ea14=ve9=22
3.2求最迟发生时间
la0=vl1-3=3、la1=vl2-4=0、la2=vl3-2=13
la3=vl4-1=6、la4=vl4-3=4、la5=vl4-5=14
la6=vl6-6=15、la7=vl6-8=13......
最早发生时间和最迟发生时间相同的活动就是关键活动,关键活动组成关键路径
_______________________________________________________________________
例题 判断顶点i和顶点j之间是否有路径
int DFSTrave(AGrapgh *G,int i,int j)
{
int k;
for(k=0;k<G->n;++k)
{
visit[k]=0;
}
DFS(G,i);
if(visit[j]==1)
{
return 1;
}
else
return 0;
}




