统计计算小测验

统计计算测验

一、填空题

  1. 已知 \(\{N(t):t>0\}\) 是速率为 \(3\) 的泊松过程，因此对 \(\forall t,N(t)\sim Pois(3t)\)，故 \(N(10)\sim Pois(30)\)，\(Var(N(10))=30.\)

  2. 已知 \(\{N(t):t>0\}\) 是速率为 \(\lambda(t)=\frac{1}{t+1}\) 的非齐次泊松过程，则

    \[E(N(t))=\int_0^t\frac{1}{s+1}\mathrm{~d}s=\ln(t+1) \]

    故 \(E(N(1))=\ln 2\).

  3. 用MC法估计 \(\theta=\int_0^{10}e^{3x+x^2}\mathrm{~d}x\)，R语言求解代码：

    Integral = function(a,b,n){#n表示⽣成的随机数的个数
  u = runif(n)
  x = a+(b-a)*u
  y = exp(3*x+x^2)
  z = (b-a)*mean(y)
  z
}
Integral(0,10,100000)

> Integral(0,10,100000)
[1] 1.229271e+55

  4. \(X\sim N(5,4)\)，要估计 \(E(\sin^2(X))\)，R语言求解代码：

    s = 0
N = 10000
for (i in 1:N){
  X = rnorm(1,5,2)
  s = s+(sin(X))^2
}
s/N

> s/N
[1] 0.5042506

  5. 已知 \(Var(f(X))=2\)，要使 \(E(f(X))\) 的 \(MC\) 估计 \(Z_N^{MC}\) 的均方根 \(RMSE(Z_N^{MC})\le0.01\)，需满足

    \[N\ge\frac{Var(f(X))}{\varepsilon^2}=\frac{2}{0.01^2}=20000. \]

二、算法设计题

  1. 解：提出假设

    \[H_0:X \ \text{服从均匀分布} \leftrightarrow H_1:X \ \text{不服从均匀分布} \]

    基于MC的拟合优度卡方检验算法：

    • 根据分布律 \(F\) 生成 \(n\) 个随机数 \(Y_1^{(1)},Y_2^{(1)},\cdots,Y_n^{(1)}\);
    • 计算 \(N_i^{(1)}=\{Y_j^{(1)}=i\}\) 个数；
    • 计算 \(T^{(1)}=\sum_{i=1}^k\frac{(N_i^{(1)}-np_i)^2}{np_i}\)；
    • 重复上述步骤得到 \(T^{(1)},T^{(2)},\cdots,T^{(m)}\)；
    • \(p-value\approx\frac{\{i:T^{(i)}\ge T\}个数}{m}\).

    R 代码：

    m = c(16,15,18,11)
n = sum(m)
p = c(0.25, 0.25, 0.25, 0.25)
T = sum((m-n*p)^2/(n*p))
r = 10000
TT = c()
for (i in 1:r){
  x = sample(c(1,2,3,4),replace=TRUE,n,p)
  N = table(x)
  s = sum((N-n*p)^2/(n*p))
  TT = c(TT,s)
}
p<-length(TT[TT>T])/r
p

> p
[1] 0.5921

    \(p>0.05\)，因此不拒绝原假设，认为 \(X\) 服从均匀分布.

  2. 解：提出假设

    \[H_0:数据服从 \ N(83,100)\leftrightarrow H_1:\overline{H}_0 \]

    基于 \(MC\) 的 \(Kolmogorov-Smirnov\) 检验的算法步骤：

    • 对样本数据排序

    • 令 $n $ 为样本容量

    • 计算 \(d=\max\limits_{1\le j\le n}\max\{\frac{j}{n}-F(x_{(j)}),F(x_{(j)})-\frac{j-1}{n}\}\)

    • for \(i=1,2,\cdots,m\) do

      • 生成 \(n\) 个随机数 \(u_1,u_2,\cdots,u_n\sim U[0,1]\)
      • 从小到大排序 \(u_{(1)}\le u_{(2)}\le\cdots\le u_{(n)}\)
      • 计算 \(D_i=\max\limits_{1\le j\le n}\max\{\frac{j}{n}-u_{(j)},u_{(j)}-\frac{j-1}{n}\}\)

    • end for

    • \(p=\frac{\#\{i:D_i>d\}}{m}\)

    • return \(p\)

    R 代码：

    x = c(89,76,80,82,83,90,79,93,85)
x = sort(x)
n = length(x)
d = max(1:n/n-pnorm(x,83,10),pnorm(x,83,10)-0:(n-1)/n)
r = 10000
D = 0
for(i in 1:r){
  u = runif(n)
  y = sort(u)
  D[i] = max(1:n/n-y,y-0:(n-1)/n)
}
p = length(D[D>d])/r
p

> p
[1] 0.5884

    \(p>0.05\)，因此不拒绝原假设，认为 \(X\) 服从 \(N(83,100)\).

  3. 解：算法步骤如下

    输入：函数 \(f\)，密度函数 \(\varphi,\psi\)，样本量 \(N\)

    输出：\(E(f(X))\) 的重要估计 \(Z_N^{IS}\)

    • \(s\gets 0\)
    • for \(j\gets 1,2,\cdots,N\) do
      • 生成 \(Y_j\sim\psi\)
      • \(s\gets s+f(Y_j)\frac{\varphi(Y_j)}{\psi(Y_j)}\)
    • end for
    • return \(s/N\)

    R代码：

    s = 0
N = 100000
for (j in 1:N){
  y = runif(1)
  s = s+sin(y)*dbeta(y,2,3)
}
s/N

> s/N
[1] 0.3816631

  4. 解：独立抽样算法步骤如下

    输入：概率密度 \(\pi(\cdot),p(·),X_0\in S,\pi(X_0)>0.\)

    输出：平稳分布为 \(\pi\) 的马尔可夫链样本

    • for \(j=1,2,\cdots\) do
      • 生成 \(Y_j\sim p(·)\)
      • 生成 \(U_j\sim U[0,1]\)
      • if \(U_j\le\alpha(X_{j-1},Y_j)\) then
        • \(X_j\gets Y_j\)
      • else
        • \(X_j\gets X_{j-1}\)
      • end if
    • end for

    R 代码（选择推荐分布 \(p(·)\) 为标准正态分布）

    # 定义 alpha(x,y)
alpha = function(x,y){
	pix = 1/(pi*(1+x^2))
	piy = 1/(pi*(1+y^2))
	px = dnorm(x,0,1)
	py = dnorm(y,0,1)
	res = min(piy*px/(pix*py),1)
}

# 独立抽样算法
x = c(); x[1] = 1
for (j in 2:10){
	y = rnorm(1,0,1)
	u = runif(1)
	if (u<=alpha(x[j-1],y)){
		x[j] = y
	} else {
		x[j] = x[j-1]
	}
}
x

> x
 [1]  1.00000000  0.70244254 -0.12929295
 [4] -0.61161516 -0.07485748 -1.61783989
 [7] -1.38897980 -1.49190060  0.45195079
[10] -0.24026176

三、统计计算题

  1. 解：已知 \(p(x)=\frac{x}{4},1<x<3\)，于是当 \(1<x<3\) 时，分布函数为

    \[F(x)=\int_1^x\frac{t}{4}\mathrm{~d}t=\frac{x^2-1}{8},\quad 1<x<3 \]

    因此 \(x=F^{-1}(u)=\sqrt{8u+1}\)，下面用R模拟产生8个随机数

    random_1 = function(n){
  x = c()
  for (i in 1:n){
    u = runif(1)
    x[i] = sqrt(8*u+1)
  }
  x
}
random_1(8)

> random_1(8)
[1] 2.383907 2.988708 1.725695 2.288825
[5] 1.975170 2.689363 1.168172 1.621312

  2. 解：已知 \(p(x)=\frac{1}{12}(3x^2+2x), \ 0<x<2\)，显然 \(p(x)\) 在 \((0,2)\) 上大于 \(0\)，因此可取 \(g(x)=1/2, \ 0<x<2\)，则 \(\frac{p(x)}{g(x)}=\frac{1}{6}(3x^2+2x)\)，显然该函数在 \((0,2)\) 上单调递增，即 \(\frac{p(x)}{g(x)}<\frac{p(2)}{g(2)}, \ \forall x\in(0,2)\)，因此取 \(c=\frac{p(2)}{g(2)}=\frac{8}{3}\)，于是 \(\frac{p(x)}{cg(x)}=\frac{1}{16}(3x^2+2x)\). 下面用 R 求解

    random<-function(n){
  x<-c()
  for (i in 1:n){
    y<-runif(1,0,2)
    u<-runif(1)
    while (u>(3*y^2+2*y)/16) {
      y<-runif(1,0,2)
      u<-runif(1)
    }
    x[i]<-y
  }
  x
}
random(7)

> random(7)
[1] 1.279676 1.584644 1.944869 1.438600
[5] 1.281554 1.821623 1.704952

  3. 解：已知 \(p(x)=0.2\exp(2)+0.8U[2,6]\). 首先生成随机数 \(Y\sim Q\)，其中

    状态 1 2
    p 0.2 0.8

    生成随机数 \(X_1\sim \exp(2),X_2\sim U[2,6]\)

    p = c(0.2,0.8)
x = c()
for (i in 1:6){
  y = sample(1:2,1,prob=p)
  if (y == 1){
    x[i] = rexp(1,2)
  } else {
    x[i] = runif(1,2,6)
  }
}
x

> x
[1] 2.24797758 4.95500782 0.02316482 3.39119376
[5] 5.21569053 2.85968540

四、综合应用题

解：由题设 \(Y\sim N(1,\sigma^2)\)，令 \(y=(y_1,y_2,\cdots,y_n)\)，则 \(y=(y_1,y_2,\cdots,y_n)\) 的似然函数为

\[p(y_1,y_2,\cdots,y_n|\sigma^2)=\prod_{i=1}^np(y_i|\sigma^2) \]

由贝叶斯公式， \(\sigma^2\) 的后验分布的密度为

\[\begin{aligned} p(\sigma^2|y)&\propto\prod_{i=1}^np(y_i|\sigma^2)p(\sigma^2)\\ &=\prod_{i=1}^n\frac{1}{\sqrt{2\pi}\sigma}\exp\left\{-\frac{(y_i-1)^2}{2\sigma^2}\right\}\cdot e^{-\sigma^2}\\ &=\frac{1}{(2\pi\sigma^2)^{n/2}}\exp\left\{-\frac{\sum_{i=1}^n(y_i-1)^2}{2\sigma^2}\right\}\cdot e^{-\sigma^2}\\ &=\frac{1}{(2\pi\sigma^2)^{n/2}}\exp\left\{-\frac{\sum_{i=1}^n(y_i-1)^2}{2\sigma^2}-\sigma^2\right\}\\ &\propto\frac{1}{(\sigma^2)^{n/2}}\exp\left\{-\frac{\sum_{i=1}^n(y_i-1)^2}{2\sigma^2}-\sigma^2\right\} \end{aligned} \]

下面用 R 模拟

# 定义sigma^2密度
pp = function(s,y){
  n = length(y)
  res = 1/(s^(n/2))*exp(-sum((y-1)^2)/(2*s)-s)
  res
}
# 定义alpha函数
alpha = function(s1,s2,y){
  if (s1>0 & s2>0) z = min(pp(s2,y)/pp(s1,y),1)
  else z = 0
  z
}

#定义random walk metropolis 算法函数
rand_Metro = function(n,sigma,y){
  s = c()
  s[1] = 0.5
  for (i in 2:n) {
    epsilon = rnorm(1,0,sigma)
    ss = s[i-1]+epsilon
    u = runif(1)
    z = alpha(s[i-1],ss,y)
    # print(z)
    if(u <= z) {
      s[i] = ss
    } else {
      s[i] = s[i-1]
    }
  }
  s
}

y = c(2,0.5,1.1)
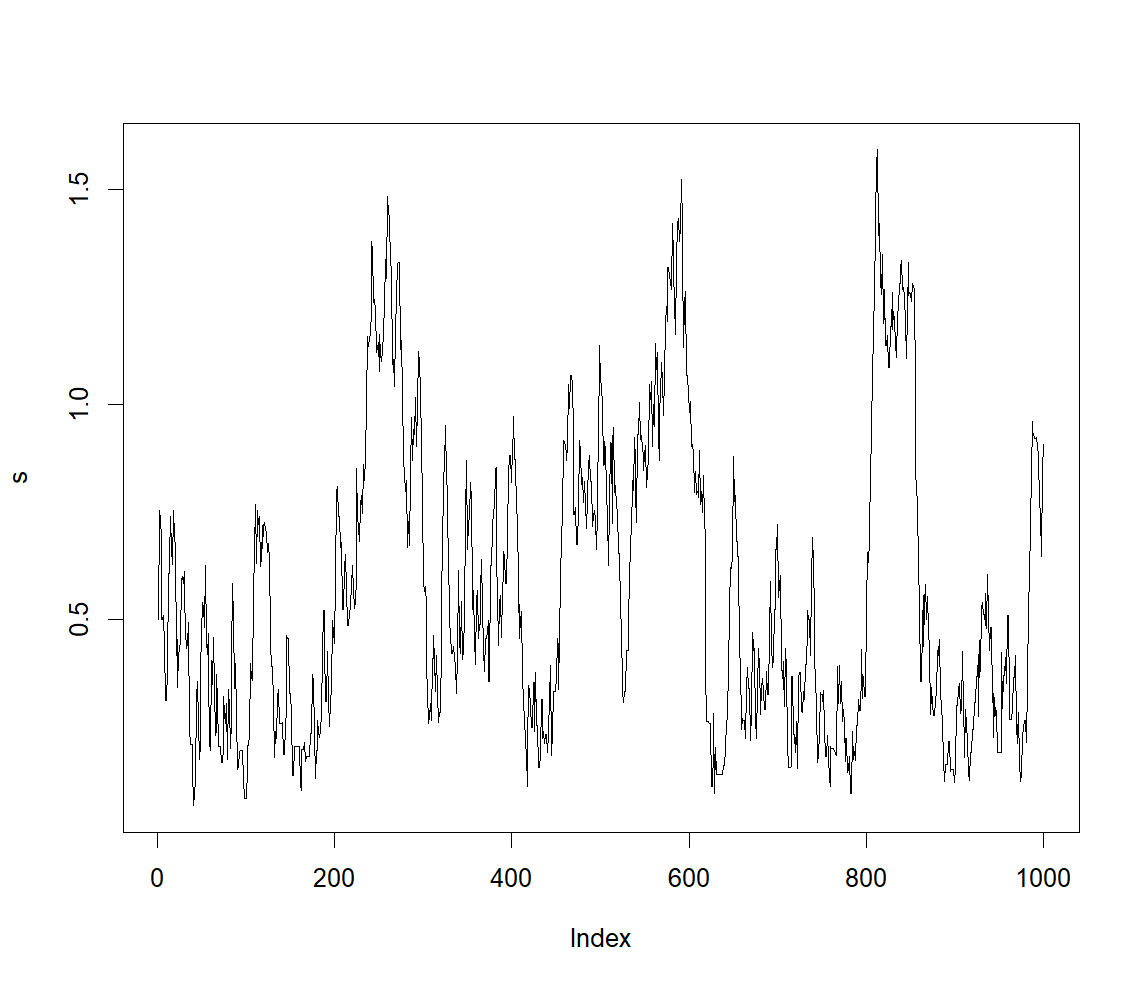
s = rand_Metro(1000,0.1,y)
plot(s,type='l')
mean(s)
var(s)

> mean(s)
[1] 0.5735499
> var(s)
[1] 0.1205141

posted @ 2023-06-07 11:03  只会加减乘除  阅读(129)  评论(0)  编辑  收藏  举报