层次分析法—基于R

本文以应用为主，原理不深究.

基本流程

Step1. 构造层次结构图（目标、准则、方案）
例如：

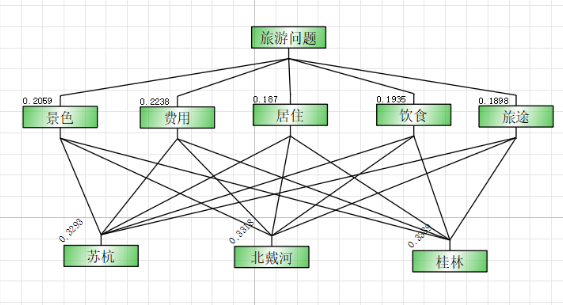
Step2. 构造成对比较矩阵
比较尺度 $a_{ij}$ 的含义

$X_i$ 与 $X_j$ 的比较尺度 $a_{ij}$	含义
1	$X_i$ 与 $X_j$ 的重要性相同
3	$X_i$ 比 $X_j$ 稍微重要
5	$X_i$ 比 $X_j$ 重要
7	$X_i$ 比 $X_j$ 明显重要
9	$X_i$ 比 $X_j$ 绝对重要
2, 4, 6, 8	$X_i$ 与 $X_j$ 重要性在两个相邻等级之间
1, 1/2, ···, 1/9	$X_i$ 与 $X_j$ 的重要性比较和以上结果相反

Step3. 一致性检验和权向量的计算
一致性指标：

$$CI = \frac{\lambda-n}{n-1}$$

其中 $\lambda$ 为成对比较矩阵的最大特征根，为了能用 $\lambda$ 对应的特征向量作为权向量 $w$

引入随机一致性指标 $RI$ （随机模拟大量正互反阵的一致性指标的平均值得到的）

n	1	2	3	4	5	6	7	8	9	10
RI	0	0	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49

当

$$CR = \frac{CI}{RI} < 0.1$$

则认为不一致性在允许范围之内，即一致性检验通过. 如果一致性检验不通过，则需要对成对比较矩阵进行修正或者重新构造成对比较矩阵.

若一致性检验通过，则认为 $\lambda$ 对应的特征向量可以作为权向量 $w$.

Step4. 计算综合权重

由上一步我们可以了准则层对目标层的权重 $w_0$，以及方案层对准则层的权重 $w_1,w_2,\cdots,w_n$ ($n$ 为准则层的元素个数).

构造 $W = [w_1,w_2,\cdots,w_n]$，则可以得到方案层对目标层的综合权重为

$$W^{(0)} = Ww_0$$

由此可以得到优劣顺序.

实例

计划在三个候选房中买一套住房，考虑的因素有交通条件、环境因素、性价比和物业服务. 假设对这四个因素的重视程度可以用成对比较矩阵

$$A = \left[ \begin{array}{c} 1 & 4 & \frac{1}{5} & 2\\ \frac{1}{4} & 1 & \frac{1}{7} & 1\\ 5 & 7 & 1 & 6\\ \frac{1}{2} & 1 & \frac{1}{6} & 1 \end{array} \right]$$

另一方面，这三套候选房在四个因素之中的优劣程度可以分别用成对比较矩阵

$$B_1 = \left[ \begin{array}{c} 1 & 2 & 2\\ \frac{1}{2} & 1 & 1\\ \frac{1}{2} & 1 & 1 \end{array} \right], B_2 = \left[ \begin{array}{c} 1 & 3 & 2\\ \frac{1}{3} & 1 & \frac{1}{2}\\ \frac{1}{2} & 2 & 1 \end{array} \right], B_3 = \left[ \begin{array}{c} 1 & \frac{1}{5} & \frac{1}{4}\\ 5 & 1 & 1\\ 4 & 1 & 1 \end{array} \right], B_4 = \left[ \begin{array}{c} 1 & 2 & 3\\ \frac{1}{2} & 1 & 2\\ \frac{1}{3} & \frac{1}{2} & 1 \end{array} \right]$$

刻画，请用层次分析法得出这三套房子的优劣.

模型求解

Step1. 构造层次结构图（目标、准则、方案）

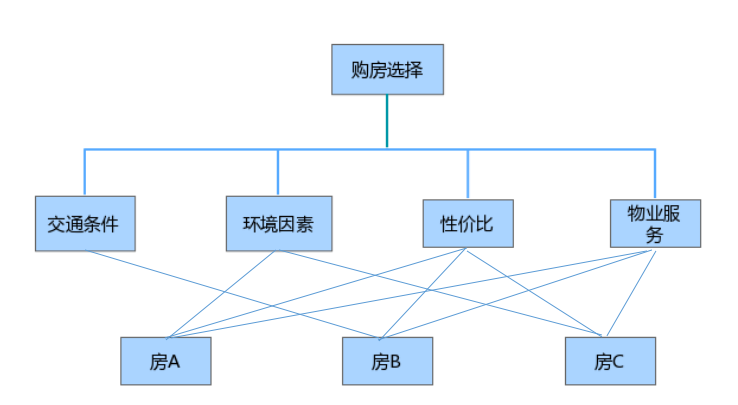
Step2. 构造成对比较矩阵

已知

$$A = \left[ \begin{array}{c} 1 & 4 & \frac{1}{5} & 2\\ \frac{1}{4} & 1 & \frac{1}{7} & 1\\ 5 & 7 & 1 & 6\\ \frac{1}{2} & 1 & \frac{1}{6} & 1 \end{array} \right]\\ B_1 = \left[ \begin{array}{c} 1 & 2 & 2\\ \frac{1}{2} & 1 & 1\\ \frac{1}{2} & 1 & 1 \end{array} \right], B_2 = \left[ \begin{array}{c} 1 & 3 & 2\\ \frac{1}{3} & 1 & \frac{1}{2}\\ \frac{1}{2} & 2 & 1 \end{array} \right], B_3 = \left[ \begin{array}{c} 1 & \frac{1}{5} & \frac{1}{4}\\ 5 & 1 & 1\\ 4 & 1 & 1 \end{array} \right], B_4 = \left[ \begin{array}{c} 1 & 2 & 3\\ \frac{1}{2} & 1 & 2\\ \frac{1}{3} & \frac{1}{2} & 1 \end{array} \right]$$

Step3. 一致性检验和权向量的计算

RI <- c('1' = 0,    '2' = 0, 
        '3' = 0.58, '4' = 0.9, 
        '5' = 1.12, '6' = 1.24, 
        '7' = 1.32, '8' = 1.41, 
        '9' = 1.45, '10' = 1.49)
 
fun1 <- function(M) {
  n <- sqrt(length(M))
  ri <- RI[n] # 对应数值n的随机一致性指标
  M_eig <- eigen(M) # 矩阵M所对应的特征根和特征向量
  value_max <- Re(M_eig$values[1]) # 最大特征值实部
  eig_vec_M = M_eig$vectors # 特征向量
  cat('特征向量为:\n')
  print(eig_vec_M) # 输出特征向量
  cat('\n')
  x_M <- eig_vec_M[,1]
  w_M <- x_M/(sum(x_M)) # 归一化
  if ((value_max-n)/(n-1) < 0.1*ri) {
    cat('一致性检验通过, 权向量为:\n')
    cat(Re(w_M)) # 输出权向量
  }
  else cat('一致性检验未通过')
}

检验成对比较矩阵 $A$:

A = matrix(c(1,1/4,5,1/2,4,1,7,1,1/5,1/7,1,1/6,2,1,6,1), ncol = 4)
fun1(A)

特征向量为:
              [,1]                    [,2]                    [,3]           [,4]
[1,] -0.2821127+0i -0.11029704+0.29898239i -0.11029704-0.29898239i  0.06265520+0i
[2,] -0.1076275+0i -0.08262200-0.06504082i -0.08262200+0.06504082i -0.06044221+0i
[3,] -0.9443907+0i  0.93948420+0.00000000i  0.93948420+0.00000000i -0.97860015+0i
[4,] -0.1302110+0i  0.02485836-0.06433420i  0.02485836+0.06433420i  0.18644788+0i
 
一致性检验通过, 权向量为:
0.1926549 0.07349887 0.644925 0.08892118

检验成对比较矩阵 $B_1$:

B1 = matrix(c(1,1/2,1/2,2,1,1,2,1,1), ncol = 3)
fun1(B1)

特征向量为:
          [,1]       [,2]       [,3]
[1,] 0.8164966 -0.9428090  0.0000000
[2,] 0.4082483  0.2357023 -0.7071068
[3,] 0.4082483  0.2357023  0.7071068
 
一致性检验通过, 权向量为:
0.5 0.25 0.25

检验成对比较矩阵 $B_2$:

B2 = matrix(c(1,1/3,1/2,3,1,2,2,1/2,1), ncol = 3)
fun1(B2)

特征向量为:
             [,1]                  [,2]                  [,3]
[1,] 0.8467969+0i  0.8467969+0.0000000i  0.8467969+0.0000000i
[2,] 0.2564554+0i -0.1282277-0.2220969i -0.1282277+0.2220969i
[3,] 0.4660103+0i -0.2330052+0.4035768i -0.2330052-0.4035768i
 
一致性检验通过, 权向量为:
0.5396146 0.1634241 0.2969613

检验成对比较矩阵 $B_3$:

B3 = matrix(c(1,5,4,1/5,1,1,1/4,1,1), ncol = 3)
fun1(B3)

特征向量为:
             [,1]                  [,2]                  [,3]
[1,] 0.1559633+0i -0.0779817+0.1350682i -0.0779817-0.1350682i
[2,] 0.7239177+0i  0.7239177+0.0000000i  0.7239177+0.0000000i
[3,] 0.6720257+0i -0.3360128-0.5819913i -0.3360128+0.5819913i
 
一致性检验通过, 权向量为:
0.1004979 0.4664699 0.4330323

检验成对比较矩阵 $B_4$:

B4 = matrix(c(1,1/2,1/3,2,1,1/2,3,2,1), ncol = 3)
fun1(B4)

特征向量为:
             [,1]                  [,2]                  [,3]
[1,] 0.8467969+0i -0.8467969+0.0000000i -0.8467969+0.0000000i
[2,] 0.4660103+0i  0.2330052-0.4035768i  0.2330052+0.4035768i
[3,] 0.2564554+0i  0.1282277+0.2220969i  0.1282277-0.2220969i
 
一致性检验通过, 权向量为:
0.5396146 0.2969613 0.1634241

Step4. 计算综合权重
由 Step3 可知一致性检验均通过，且

$$w_0 = (0.1926549, 0.07349887, 0.644925, 0.08892118)'\\ w_1 = (0.5, 0.25, 0.25)'\\ w_2 = (0.5396146, 0.1634241, 0.2969613)'\\ w_3 = (0.1004979, 0.4664699, 0.4330323)'\\ w_4 = (0.5396146, 0.2969613, 0.1634241)'$$

则 $(w_1,w_2,w_3,w_4)_{3\times 4}\times w_0$ 即为综合权重.

w_0 = c(0.1926549, 0.07349887, 0.644925, 0.08892118)
w_1 = c(0.5, 0.25, 0.25)
w_2 = c(0.5396146, 0.1634241, 0.2969613)
w_3 = c(0.1004979, 0.4664699, 0.4330323)
w_4 = c(0.5396146, 0.2969613, 0.1634241)
W = matrix(c(w_1,w_2,w_3,w_4), ncol = 4)
W %*% w_0

          [,1]
[1,] 0.2487853
[2,] 0.3874195
[3,] 0.3637953

于是三所房屋的优劣顺序为 $B, C, A$.