主成分分析—基于R
基本流程
1.检验数据是否适合做主成分分析/是否需要主成分
-
本质：数据之间相关性较高则适合做主成分分析
-
检验方法：
- KMO系数法
KMO()括号内填相关矩阵
KMO系数 > 0.7，则认为适合做主成分（0.7 并不是严格规定，实际操作中 0.6 这样也不是不行） - barlett球形检验
cortest.bartlett()括号内填相关矩阵
$ p<0.05 $ 认为适合做主成分分析
一般来说，主要看bartlett球形检验
- KMO系数法
2.主成分提取
根据相关矩阵的特征根（的平方根）大小进行权重分配
princomp(X<原始样本>, cor = T) -> X
summary(X, loading = T)
样本信息保留 80%, 85%, 90% 可做主成分（比较主观）
实例
我们有 "工业数据.csv" 文件（如下图），文件内包含不同工业部门行业指标信息，对此进行主成分分析.
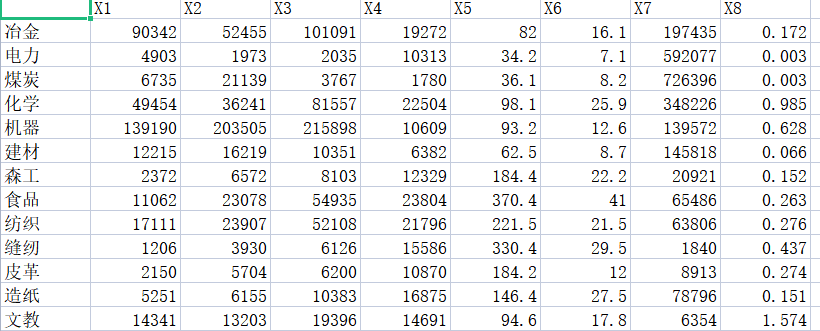
求解
Sep1. 配置主成分分析包
library(psych)
Step2. 导入数据
read.table("工业部门各行业指标.csv", sep = ",", row.names = 1, header = T) -> t
t
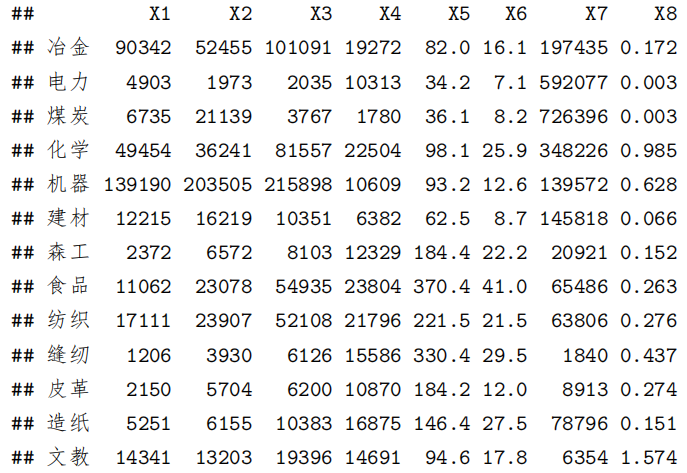
Step3. 计算相关矩阵
cor(t) -> t.cor
Step4. 检验是否适合主成分
- KMO法
KMO(t.cor)
## Kaiser-Meyer-Olkin factor adequacy
## Call: KMO(r = t.cor)
## Overall MSA = 0.46
## MSA for each item =
## X1 X2 X3 X4 X5 X6 X7 X8
## 0.54 0.44 0.42 0.35 0.55 0.62 0.39 0.48
发现 MSA = 0.46 < 0.7
- bartlett 球形检验
cortest.bartlett(t.cor, n = length(t$X1))
## $chisq
## [1] 96.95727
##
## $p.value
## [1] 1.567814e-09
##
## $df
## [1] 28
发现 \(p << 0.05\)
虽然 KMO 检验未通过，但是 bartlett 检验通过了，可以认为适合做主成
分.
Step5. 主成分提取
princomp(t, cor = T) -> t.pca
summary(t.pca, loadings = T)
## Importance of components:
## Comp.1 Comp.2 Comp.3
## Standard deviation 1.7620762 1.7021873 0.9644768
## Proportion of Variance 0.3881141 0.3621802 0.1162769
## Cumulative Proportion 0.3881141 0.7502943 0.8665712
## Comp.4 Comp.5 Comp.6
## Standard deviation 0.80132532 0.55143824 0.29427497
## Proportion of Variance 0.08026528 0.03801052 0.01082472
## Cumulative Proportion 0.94683649 0.98484701 0.99567173
## Comp.7 Comp.8
## Standard deviation 0.179400062 0.0494143207
## Proportion of Variance 0.004023048 0.0003052219
## Cumulative Proportion 0.999694778 1.0000000000
##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
## X1 0.477 0.296 0.104 0.184 0.758 0.245
## X2 0.473 0.278 0.163 -0.174 -0.305 -0.518 0.527
## X3 0.424 0.378 0.156 -0.174 -0.781
## X4 -0.213 0.451 0.516 0.539 -0.288 -0.249 0.220
## X5 -0.388 0.331 0.321 -0.199 -0.450 -0.582 0.233
## X6 -0.352 0.403 0.145 0.279 -0.317 0.714
## X7 0.215 -0.377 0.140 0.758 -0.418 -0.194
## X8 0.273 -0.891 -0.322 -0.122
结果解释：
- Standard deviation: 第一个主成分特征根的标准差
- Proportion of Variance: 第一个主成分在所有特征跟平方根的占比（权重）
- Cumulative Proportion: 之前所有主成分占比，因此最后一定是1
- 一般所示样本不超过1/4，记主成分占比达85%或90%以上，这个比较主观的
- loadings（因子载荷）显示的是主成分权重信息
- 第一个主成分 \(z_1(Comp.1) = 0.477x_1 + 0.473x_2 + \cdots + 0.215x_7\). 以此类推
前四个主成分保留了 94.68% 的原始数据信息，因此不妨取前四个为主成分
Step6. 数据标准化
\[x_{ij} = \frac{x_{ij}-\bar{x}_j}{\sigma(x_j)}
\]
scale(t) -> t.s
Step7. 计算各主成分得分
as.matrix(t.s) %*% t.pca$loadings -> temp
## Comp.1 Comp.2 Comp.3 Comp.4
## 冶金 1.4752359 0.7586330 0.53804346 0.48981582
## 电力 0.4982149 -2.5916439 0.22831171 0.85190555
## 煤炭 1.0564432 -3.2255272 0.40941148 0.58246589
## 化学 0.4598646 1.1836386 -0.99768111 1.59955537
## 机器 4.5284817 2.2624411 0.46764480 -0.75806395
## 建材 0.3299732 -1.7736147 0.03113872 -0.93799882
## 森工 -1.1025047 -0.3179334 0.28182618 -0.69170879
## 食品 -2.1949756 2.2441391 1.09921449 0.55675111
## 纺织 -0.8411700 0.8956587 0.35286803 0.12852355
## 缝纫 -2.0318632 0.8251577 0.23105405 -0.51413084
## 皮革 -0.7133301 -0.7556065 -0.12255137 -1.11097884
## 造纸 -1.2014056 0.0303427 0.28702019 0.08174798
## 文教 -0.2629643 0.4643149 -2.80630062 -0.27788402
Step8. 对目标进行评价，计算得分
t.pca$sdev * temp -> t.fix
apply(t.fix[, 1:4], 1, sum) -> df
df
## 冶金 电力 煤炭 化学 机器
## 3.5032972 2.1515980 2.1615593 3.8545210 6.0625568
## 建材 森工 食品 纺织 缝纫
## -2.2161595 -0.1660242 3.2265730 -0.9075561 -4.1959795
## 皮革 造纸 文教
## -2.7935976 -0.7764028 -0.0840824
得出排名
sort(length(t$X1) + 1 - rank(df))
## 机器 化学 冶金 食品 煤炭 电力 文教 森工 造纸 纺织 建材 皮革
## 1 2 3 4 5 6 7 8 9 10 11 12
## 缝纫
## 13
结论
排名为
| 行业 | 机器 | 化学 | 冶金 | 食品 | 煤炭 | 电力 | 文教 | 森工 | 造纸 | 纺织 | 建材 | 皮革 | 缝纫 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 排名 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
