遗传算法详解及c++实现

1、什么是遗传算法？

遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。遗传算法是从代表问题可能潜在的解集的一个种群开始的，而一个种群则由经过基因编码的一定数目的个体组成。每个个体实际上是染色体带有特征的实体。染色体作为遗传物质的主要载体，即多个基因的集合，其内部表现（即基因型）是某种基因组合，它决定了个体的形状的外部表现，如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。因此，在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂，我们往往进行简化，如二进制编码，初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度大小选择比较优秀的个体，并借助于自然遗传学的遗传算子进行交叉和变异，产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码，可以作为问题近似最优解。

2、遗传算法的运算过程

(a)初始化：设置进化代数计数器t=0，设置最大进化代数T，随机生成M个个体作为初始群体P(t)。

(b)个体评价：计算群体P(t)中各个个体的适应度。

(c)选择运算：将选择算子作用于群体。选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的。

(d)交叉运算：将交叉算子作用于群体。遗传算法中起核心作用的就是交叉算子。

(e)变异运算：将变异算子作用于群体。即是对群体中的个体串的某些基因座上的基因值作变动。群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t+1)。

(f)终止条件判断：若t=T,则以进化过程中所得到的具有最大适应度个体作为最优解输出，终止计算。

3、遗传算法基本框架

 

4、相关术语

基因型(genotype)：性状染色体的内部表现；

表现型(phenotype)：染色体决定的性状的外部表现，或者说，根据基因型形成的个体的外部表现；

进化(evolution)：种群逐渐适应生存环境，品质不断得到改良。生物的进化是以种群的形式进行的。

适应度(fitness)：度量某个物种对于生存环境的适应程度。

选择(selection)：以一定的概率从种群中选择若干个个体。一般，选择过程是一种基于适应度的优胜劣汰的过程。

复制(reproduction)：细胞分裂时，遗传物质DNA通过复制而转移到新产生的细胞中，新细胞就继承了旧细胞的基因。

交叉(crossover)：两个染色体的某一相同位置处DNA被切断，前后两串分别交叉组合形成两个新的染色体。也称基因重组或杂交；

变异(mutation)：复制时可能（很小的概率）产生某些复制差错，变异产生新的染色体，表现出新的性状。

编码(coding)：DNA中遗传信息在一个长链上按一定的模式排列。遗传编码可看作从表现型到基因型的映射。

解码(decoding)：基因型到表现型的映射。

个体（individual）：指染色体带有特征的实体；

种群（population）：个体的集合，该集合内个体数称为种群

 

5、遗传算法的应用实例

现在我以一个多元函数最值问题求解来一步步阐述遗传算法的实现过程。

问题：求一个多元函数的最大值，f(x1,x2) = 21.5+x1*sin(4pi*x1)+x2*sin(20pi*x2)，其中-3.0≤x1≤12.1,4.1≤x2≤5.8。

6、设计与实现

(a)前提条件：

const int Po_Size = 50;//种群规模
const int Ev_Algebra = 500;//进化代数
const double Ov_Probability = 0.850; //交叉概率,交叉概率用于判断两两个体是否需要交叉
const double Va_Probability = 0.050;//变异概率,变异概率用于判断任一个体是否需要变异
const int De_Variable = 2;//函数自变量的个数,如果要进行多元函数的最值求解，直接修改自变量数个De_Variable即可

vector<Individual> nowpopulation;//P(t)种群
vector<Individual> midpopulation;//中间种群，存放轮盘选择后的优秀个体
vector<Individual> nextpopulation;//P(t+1)种群

 

(b)类的实现：

class Individual //定义个体类
{
private:
double Variable[De_Variable];//存放变量x1,x2,x3........
double Fitness;//适应值
double ReFitness;//适应值概率
double SumFitness;//累加概率，为轮盘转做准备
public：

............

};

(c)：初始化：

随机生成两个满足条件范围的x1和x2自变量，生成一个个体，初始化种群，得到第一代种群。在这里用一个随机函数生成两个指定范围的小数，然后创建一个对象（个体），加入到初始种群中，直到达到种群规模。

(d)计算适应值，适应值概率，累加概率：
适应值是根据每个个体的自变量进行计算的，这里是求函数的最大值，所以把函数就作为适应值计算函数，适应值概率的计算是每个个体占所有个体适应值总和的百分比，累加概率是为了轮盘法选择做准备。

(e)进行选择，杂交，变异：

最重要的就是这三个算子，选择即就是用轮盘法选出一些相对优秀的个体，在程序中我没有用精英制选择，读者自己可以加以实现。杂交之前需要对自变量进行编码，我在程序中采用的是二进制的编码，用的是c++标准库中的bitset类来进行编码的，杂交的方式我用的是单点杂交，你也可以选择其他杂交方式。变异我用的是基本位变异方式，相对比较简单。

c++code:

GeneticAlgorithm.h文件

//功能：求一个多元函数的最大值（这里是求二元函数的最大值：f(x1,x2) = 21.5+x1*sin(4pi*x1)+x2*sin(20pi*x2)）
#pragma once//保证文件只被编译一次
#include<random>
#include<vector>
#include<iostream>
#include<cmath>
#include<ctime>
#include <cstdlib>
#include <bitset>
#include<iomanip>
using namespace std;
const double PI = 3.141592653589793;//定义一个不可改变的常量值PI
const int Po_Size = 50;//种群规模
const int Ev_Algebra = 500;//进化代数
const double Ov_Probability = 0.850; //交叉概率,交叉概率用于判断两两个体是否需要交叉
const double Va_Probability = 0.050;//变异概率,变异概率用于判断任一个体是否需要变异
const int De_Variable = 2;//函数自变量的个数,如果要进行多元函数的最值求解，直接修改自变量数个De_Variable即可
const int length1 = 24;//精确到6位小数，用24位二进制编码
const int length2 = 23;//精确到6位小数，用23位二进制编码
class X_Range //自变量取值范围类，适用于多个变量
{
private:
    double Upper;//变量的上界取值
    double Lower;//变量的下界取值
public:
    X_Range(double m_Upper, double m_Lower);//构造函数
    double GetUpper()const;//获取变量上限
    double GetLower()const;//获取变量下限
};
class Individual //定义个体类
{
private:
    double Variable[De_Variable];//存放变量x1,x2,x3........
    double Fitness;//适应值
    double ReFitness;//适应值概率
    double SumFitness;//累加概率，为轮盘转做准备
public:
    Individual() {}//默认构造函数
    Individual(double* m_Variable);//构造函数
    double* GetVariable();//获取变量值
    void ChaFitness(const double m_fitness);//修改适应值
    void ChaReFitness(const double m_ReFitness);//修改适应值概率
    void ChaSumFitness(const double m_SumFitness);//修改累加概率
    double GetFitness()const;//获取适应值
    double GetReFitness()const;//获取适应值概率
    double GetSumFitness()const;//获取累加概率
};
void Initialize();//随机初始化种群，得到第一代个体 
void CaculaFitness();//计算个体的适应值
void CaculaReFitness();//计算个体的适应值概率
void CalculaSumFitness();//计算累加个体概率
void seclect();//种群选择
double Scand();//随机产生0到49的随机整数
void crossing();//杂交
void variating();//变异
void genetic_algorithm();//遗传算法

GeneticAlgorithm.cpp文件

#include"GeneticAlgorithm.h"//包含头文件
//自变量取值范围向量和种群向量定义
const X_Range Range[De_Variable] = { X_Range(-3.0,12.1) ,X_Range(4.1,5.8) };//自变量（或者基因）x1,x2的取值范围
vector<Individual> nowpopulation;//P(t)种群
vector<Individual> midpopulation;//中间种群，存放轮盘选择后的优秀个体
vector<Individual> nextpopulation;//P(t+1)种群
//X_Range类实现
X_Range::X_Range(double m_Lower, double m_Upper) :Lower(m_Lower), Upper(m_Upper){}//X_Range类构造函数实现
double X_Range::GetUpper()const//获取变量上限
{
    return Upper;
}
double X_Range::GetLower()const//获取变量下限
{
    return Lower;
}
//Individual类实现
Individual::Individual(double* m_Variable)//构造函数
{
    for (int i = 0; i < De_Variable; i++)//用for循环自变量逐个赋值
    {
            if (m_Variable[i] >= Range[i].GetLower() && m_Variable[i] <= Range[i].GetUpper())//这里要进行自变量取值范围判断 
            {
                Variable[i] = m_Variable[i];//自变量赋值
            }
            else//不满足要求则发出出错警告并返回
            {
                cerr << "自变量取值不满足要求" << endl;
                exit(1);//停止程序，我会以随机函数的方式生成自变量的值(基因值)，这里说明基因值不在规定范围内
            }
    }
    //初始化时默认适应值等值为0
    this->Fitness = 0;
    this->ReFitness = 0;
    this->SumFitness = 0;
}
double* Individual::GetVariable()//获取基因值
{
    return Variable;
}
double Individual::GetFitness()const//获取适应值
{
    return Fitness;
}
double Individual::GetReFitness()const //获取适应值概率
{
    return ReFitness;
}
double Individual::GetSumFitness()const//获取累加概率
{
    return SumFitness;
}
void Individual::ChaFitness(const double m_fitness)//修改适应值
{
    this->Fitness = m_fitness;
}
void Individual::ChaReFitness(const double m_ReFitness)//修改适应值概率
{
    this->ReFitness = m_ReFitness;
}
void Individual::ChaSumFitness(const double m_SumFitness)//修改累加概率
{
    this->SumFitness = m_SumFitness;
}
//遗传算法的准备工作
void Initialize()//随机初始化种群，得到第一代种群
{
//产生指定范围的随机变量（基因）
    double X[Po_Size][De_Variable];//为了使程序可以满足多元函数最值的计算，用矩阵保存产生的随机数变量值
    for (int j = 0; j < De_Variable; j++)
    {
        default_random_engine e(time(0));//引擎，生成随机序列
        uniform_real_distribution<double> u(Range[j].GetLower(), Range[j].GetUpper());//分布
        for (int i = 0; i < Po_Size; i++)//先按列存储随机数
        {
            X[i][j] = u(e);//循环结束时，所有随机值就保存在X矩阵中
        }
    }
//生成对象（染色体）并加入到初始种群中
    for (int i = 0; i < Po_Size; i++)
    {
        double variable[De_Variable];
        for (int j = 0; j < De_Variable; j++)
        {
            variable[j] = X[i][j];//按行保存
        }
        Individual Indivi(variable);//生成一个对象（染色体）
        nowpopulation.push_back(Indivi);//加入到种群population中
    }
}
void CaculaFitness()//计算个体的适应值
{
    //f(x1,x2) = 21.5+x1*sin(4pi*x1)+x2*sin(20pi*x2)）为适应度计算函数
    double fitness = 0;//临时适应值
    double x[De_Variable];//临时存储自变量（基因）
    for (int i = 0; i < Po_Size; i++)
    {
        for (int j = 0; j < De_Variable; j++)
            x[j] = nowpopulation.at(i).GetVariable()[j];//这样更直观
        fitness = 21.5 + x[0] * sin(4 * PI*x[0]) + 2 * sin(20 * PI*x[1]);//适应度计算
        nowpopulation.at(i).ChaFitness(fitness);//修改当前染色体的适应值
    }
}
void CaculaReFitness()//计算适应值概率
{
    double sum = 0;//适应值累加器
    double temp = 0;
    for (int i = 0; i < Po_Size; i++)//计算出适应值之和
    {
        sum += nowpopulation.at(i).GetFitness();
    }
    for (int j = 0; j < Po_Size; j++)
    {
        temp = nowpopulation.at(j).GetFitness() / sum;//计算概率
        nowpopulation.at(j).ChaReFitness(temp);//修改个体的适应度概率
    }
}
void CalculaSumFitness()//计算累加个体概率
{
    double summation = 0;//累加器
    for (int k = 0; k < Po_Size; k++)
    {
        summation += nowpopulation.at(k).GetReFitness();
        nowpopulation.at(k).ChaSumFitness(summation);//当前累加结果赋值
    }
}
void seclect() //种群选择
{
    //随机生生成0到1的小数
    double array[Po_Size];//随机数保存变量
    default_random_engine e(time(0));//引擎，生成随机序列
    uniform_real_distribution<double> u(0.0, 1.0); //分布
    for (int i = 0; i < Po_Size; i++)
        array[i] = u(e);
    //轮盘进行选择
    for (int j = 0; j < Po_Size; j++)
    {
        for (int i = 1; i < Po_Size; i++)
        {
            if (array[j] < nowpopulation[i - 1].GetSumFitness())
            {
                midpopulation.push_back(nowpopulation.at(i - 1));//加入到中间种群
            }
            if (array[j] >= nowpopulation.at(i - 1).GetSumFitness() && array[j] <= nowpopulation.at(i).GetSumFitness())
            {
                midpopulation.push_back(nowpopulation.at(i));//加入到中间种群
            }
        }
    }
    nowpopulation.clear();//清空nowpopulation
} 
double Scand() //随机产生0到1的小数
{
    int N = rand() % 999;
    return double(N)/1000.0;;//随机产生0到1的小数
}
void crossing()//杂交
{
    int num = 0;//记录次数
    double corss = 0.0;//保存随机产生的概率值
    srand((unsigned)time(NULL));//根据系统时间设置随机数种子,设置一次随机种子就行
    double array1[De_Variable], array2[De_Variable];//临时存储父亲和母亲的变量值
    while (num< Po_Size-1)//个体1与个体2杂交，个体3与个体4杂交......个体i和个体i+1杂交
    {
        //判断双亲是否需要杂交，随机生成一个0到1的小数，如果这个数大于杂交概率，则放弃杂交，直接遗传给下一代，否则，对父母体进行杂交
        corss = Scand();
        if (corss <= Ov_Probability)//如果corss小于等于杂交概率Ov_Probability就进行单点杂交
        {
            //首先寻找对应下标的个体并且保存
            for (int i = 0; i < De_Variable; i++)
            {
                array1[i] = midpopulation.at(num).GetVariable()[i];//父亲的自变量
                array2[i] = midpopulation.at(num + 1).GetVariable()[i];//母亲自变量
            }
            int localx1, localx2;//记录基因交叉点的位置
            int corssx1[length1], corssx2[length2];//作为交换基因的数组
            double newx1[2], newx2[2];//分别用来保存基因交换后所对应自变量值
            bool p1 = true, p2 = true;
            //然后对双亲变量进行编码并且进行单点杂交
            for (int j = 0; j < De_Variable; j++)//array1的x1编码之后和array2的x1编码后进行单点杂交，以此类推
            {
                if (j == 0)//x1进行编码并且杂交
                {
                    bitset<length1> array1b1((array1[j] + 3.0)* pow(10, 6));//加上3.0形成一个unsigaed数之后在进行母体1的x1编码
                    bitset<length1> array2b1((array2[j] + 3.0)* pow(10, 6));//加上3.0形成一个unsigaed数之后在进行母体2的x1编码        
                    //现在随机生成0到length1-1的数，确定交叉点的位置
                    localx1 = rand() % length1;
                    //现在进行单点交叉，交换双亲localx1后面的基因
                    for (int i = 0; i < localx1; i++)
                        corssx1[i] = array1b1[i];
                    for (int k = 0; k < localx1; k++)
                        array1b1[k] = array2b1[k];
                    for (int s = 0; s < localx1; s++)
                        array2b1[s] = corssx1[s];
                    //新值保存在newx1数组中，x1基因完成单点杂交操作
                    newx1[0] = double(array1b1.to_ullong()) / pow(10, 6) - 3.0;
                    newx2[0] = double(array2b1.to_ullong()) / pow(10, 6) - 3.0;
                    //对新产生的值进行判断，判断是否超出范围，如果超出范围则不杂交
                    if (newx1[0]< Range[0].GetLower() || newx1[0]>Range[0].GetUpper() || newx2[0]<Range[0].GetLower() || newx2[0]>Range[0].GetUpper())
                    {
                        p1 = false;
                        break;
                    }
                }
                if (j == 1)//x2进行编码并且杂交
                {
                    bitset<length2> array1b2((array1[j]) * pow(10, 6));//母体1的x2编码
                    bitset<length2> array2b2((array2[j]) * pow(10, 6));//母体2的x2编码
                    //现在随机生成0到length2-1的数，确定交叉点的位置
                    localx2 = rand() % length2;
                    //现在进行单点交叉，交换双亲localx2后面的基因
                    for (int i = 0; i < localx2; i++)
                        corssx2[i] = array1b2[i];
                    for (int k = 0; k < localx2; k++)
                        array1b2[k] = array2b2[k];
                    for (int s = 0; s < localx2; s++)
                        array2b2[s] = corssx2[s];
                    //新值保存在newx2数组中，x2基因完成单点杂交操作
                    newx1[1] = double(array1b2.to_ullong()) / pow(10, 6);
                    newx2[1] = double(array2b2.to_ullong()) / pow(10, 6);
                    //对新产生的值进行判断，判断是否超出范围，如果超出范围则不杂交
                    if (newx1[1]< Range[1].GetLower() || newx1[1]>Range[1].GetUpper() || newx2[1]<Range[1].GetLower() || newx2[1]>Range[1].GetUpper())
                    {
                        p2 = false;
                        break;
                    }
                }
            }
            if (p1 == true && p2 == true)
            {
                Individual newchiled1(newx1);
                Individual newchiled2(newx2);
                nextpopulation.push_back(newchiled1);
                nextpopulation.push_back(newchiled2);
            }
            else//将原来的个体遗传给下一代
            {
                nextpopulation.push_back(midpopulation.at(num));
                nextpopulation.push_back(midpopulation.at(num + 1));
            }
        }
        else//否则直接遗传给下一代nextpopulation
        {
            nextpopulation.push_back(midpopulation.at(num));//生成一个新的个体并且加入到nextpopulation中
            nextpopulation.push_back(midpopulation.at(num + 1));
        }    
        num += 2;
    }
    midpopulation.clear();//清空midpopulation
}
void variating()//变异
{
    int num = 0;
    while (num<Po_Size)
    {
        double variation = Scand();//随机产生一个0到1的小数，用于判断是否进行变异
        if (variation <= Va_Probability)//如果variation小于变异系数，则需要进行变异
        {
            double x[2];
            bool p = true;
            int x1local, x2local;
            x[0] = nextpopulation.at(num).GetVariable()[0];
            x[1] = nextpopulation.at(num).GetVariable()[1];
            bitset<length1> array1((x[0]+ 3.0)* pow(10, 6));//x1编码
            bitset<length2> array2(x[1]*pow(10,6));//x2编码
            x1local = rand() % length1;//array1该位取反
            x2local = rand() % length2;//array2该位取反
            array1.flip(x1local);//改变array1 x1local位的状态
            array2.flip(x2local);//改变array2 x2local位的状态
            x[0] = double(array1.to_ullong()) / pow(10, 6) - 3.0;
            x[1] = double(array2.to_ullong()) / pow(10, 6);
            //判断是否符合条件
            if (x[0]< Range[0].GetLower() || x[0]>Range[0].GetUpper() || x[1]<Range[1].GetLower() || x[1]>Range[1].GetUpper())
                p = false;
            if (!p)
                nowpopulation.push_back(nextpopulation.at(num));
            if (p)
            {
                Individual newchiled(x);
                nowpopulation.push_back(newchiled);
            }
        }
        else
            nowpopulation.push_back(nextpopulation.at(num));
        num++;
    }
    nextpopulation.clear();//清空nextpopulation
}
void genetic_algorithm() 
{
    Initialize();//初始化种群,随机生成第一代个体
    //进化500代
    for (int i = 0; i < Ev_Algebra; i++)
    {
        CaculaFitness();//适应度计算
        CaculaReFitness();//适应度概率计算
        CalculaSumFitness();//计算累加个体概率
        seclect();//选择
        crossing();//杂交
        variating();//变异
    }
    CaculaFitness();//适应度计算
    double maxfitness=nowpopulation.at(0).GetFitness();
    int maxid = 0;
    int k;
    for (k = 0; k < Po_Size; k++)
    {
        if (maxfitness < nowpopulation.at(k).GetFitness())
        {
            maxfitness = nowpopulation.at(k).GetFitness();
            maxid = k;
        }    
    }
    //进化500代之后输出
    cout << "x1"<<setw(10)<<"x2" << setw(15)<<"Fitness" << endl;
    for (int j = 0; j < Po_Size; j++)
        cout << nowpopulation.at(j).GetVariable()[0] <<setw(10)<< nowpopulation.at(j).GetVariable()[1] << setw(10) <<nowpopulation.at(j).GetFitness() << endl;
    cout << "x1=" << nowpopulation.at(maxid).GetVariable()[0] << " ，" << "x2=" << nowpopulation.at(maxid).GetVariable()[1] << "时取得最大值：" << maxfitness << endl;
}

main.cpp文件

#include"GeneticAlgorithm.h"
int main()
{
    genetic_algorithm();
    system("pause");
    return 0;
}

结果：

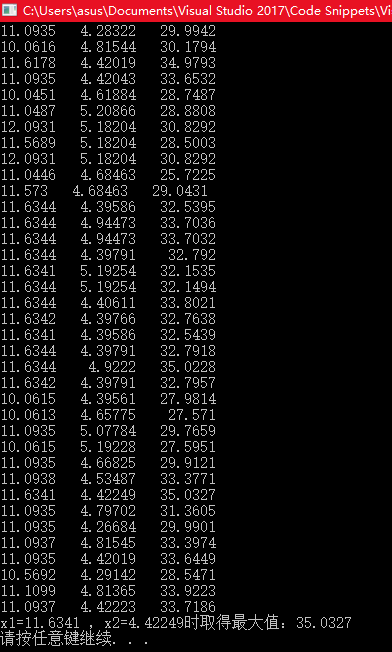
遗传算法的细节我就没有过多的介绍，上面的代码是本人根据f(x1,x2) = 21.5+x1*sin(4pi*x1)+x2*sin(20pi*x2)，其中-3.0≤x1≤12.1,4.1≤x2≤5.8写的，如果有不合理的地方，麻烦提出来，谢谢大家！