【中等】11-盛最多水的容器

题目

Given n non-negative integers a1, a2, ..., an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and n is at least 2.

给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

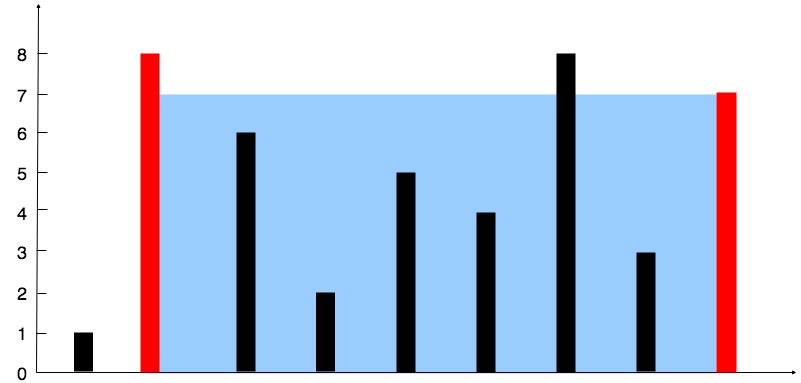
The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

Example

Input: [1,8,6,2,5,4,8,3,7]
Output: 49

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/container-with-most-water

解法

方法：双指针

解题思路

容器的容积由宽*高决定，高是由两个数字中最小的一个决定的，宽是由两个数字之间的索引差决定的，那么可以先考虑宽度最大，也就是把容器左壁设置为第一个位置，右壁设置为最后一个位置，计算容积，此时，该容积不是最大的原因是，可能有更小的宽度但是更大的高度使得总容积更大，此时想要缩减宽度，可以把两侧的内壁中的一个向内移动，如果是将较大的一侧向内移，容积不可能变大，所以将较小的一侧向内移，再次计算容积，重复过程直到左右已经无法接近，此时可以得到最大的容积。

代码

class Solution {
public:
    int maxArea(vector<int>& height) {
        int start = 0, end = height.size()-1, max_v = 0;
        while(start < end){
            if(height[start] < height[end]){
                max_v = max(max_v, height[start]*(end-start));
                start++;
            }
            else{
                max_v = max(max_v, height[end]*(end-start));
                end--;
            }
        }
        return max_v;
    }
};