【中等】56-合并区间 Merge Intervals

题目

Given a collection of intervals, merge all overlapping intervals.

给出一个区间的集合，请合并所有重叠的区间。

Example1

输入: [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

Example2

输入: [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。

来源：力扣（LeetCode）
链接：https://leetcode.com/problems/merge-intervals/

解法

方法：排序

解题思路

首先，我们使用过一个数轴来抽象区间的合并过程，对于一组区间，我们可以通过他们在数轴上的覆盖情况得到最终的区间，只要从最左覆盖的区块开始判断它与其相邻的区块是否可以合并，并逐渐向后排查就可以得到最终的所有区间

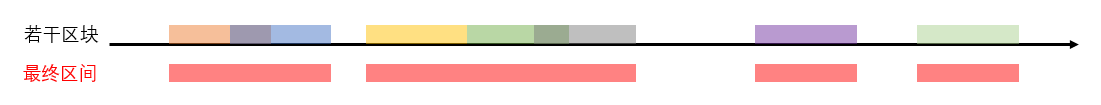
可以知道，判断两个区间是否可以合并的依据是较大起点的区间起点与较小起点的区间终点之间的关系(如果起点相同一定可以合并)。假设区间a的起点小于区间b的起点，那么如果区间b的起点<=区间a的终点，那么两个区间是可以合并的，合并的起点就是区间a的起点，合并的终点就是区间a和区间b之间较大的终点。

所以对于一组区间，只要我们按顺序对输入的区间进行合并就可以了，如对于区间1、2、... n，先把区间1当作区间a，区间2当作区间b，如果可以合并，得到的新的区间继续与区间3合并，当合并得到的新区间Inter与区间i无法合并时，区间Inter就是最终结果中的其中一个区间；此时，我们再将i作为新的区间a，i+1作为区间b重复上述过程。

但是直接这样前提是，区间1-n的起点是从小到大排列的，我们没有办法保证输入是按照起点的大小排序的，所以要先对区间进行排序，再按照上述算法进行合并得到最终的结果

代码

class Solution {
public:
    static bool comp(const vector<int> &a, const vector<int> &b){
        return a[0] < b[0];
    }
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        vector<vector<int>> res;
        sort(intervals.begin(), intervals.end(), comp); // 使用comp函数辅助排序
        int start = 0, end = 0;
        for(int i = 0;  i < intervals.size(); ++i){ // 从左到右排查数轴上的区块
            end = intervals[i][1];
            res.push_back(vector<int>(2, intervals[i][0])); // 新区间的起点一定是第一个区块的起点
            while(i<intervals.size()-1 && end >= intervals[i+1][0]){ // 下一个区块可以合并
                end = intervals[i+1][1] > end ? intervals[i+1][1] : end; // 判断当前区间的终点
                i++; // 继续判断下一个区块是否可以合并
            }
            res[res.size()-1][1] = end; // 后面已经没有可以合并的区块，就结束当前区间，从下一个区间开始找
        }
        return res;
    }
};