【中等】542-01 矩阵 01 Matrix
题目
Given a matrix consists of 0 and 1, find the distance of the nearest 0 for each cell.
The distance between two adjacent cells is 1.
- The number of elements of the given matrix will not exceed 10,000.
- There are at least one 0 in the given matrix.
- The cells are adjacent in only four directions: up, down, left and right.
给定一个由 0 和 1 组成的矩阵,找出每个元素到最近的 0 的距离。
两个相邻元素间的距离为 1
- 给定矩阵的元素个数不超过 10000。
- 给定矩阵中至少有一个元素是 0。
- 矩阵中的元素只在四个方向上相邻: 上、下、左、右。
Example1
输入
0 0 0
0 1 0
0 0 0
输出
0 0 0
0 1 0
0 0 0
Example2
输入
0 0 0
0 1 0
1 1 1
输出
0 0 0
0 1 0
1 2 1
解法
方法一:广度优先搜索
解题思路
对于这样的01矩阵,首先可以判断的是如果矩阵位置上的数值为0,那么距离是0,如果位置上是1,其周围如果有0,那么距离就是1,如果周围没有0,那么就要由其周围的1的最小距离决定了。
可以认为,如果已知0的位置,其周围所有的1的最小距离都是1,这些1周围的1的最小距离都是2,也就是说可以从距离为0开始逐渐递增,根据距离找到所有的点。也就是广度优先搜索的思想。
所以,我们先遍历矩阵找到所有的0,将这些0的位置信息存储到队列中,再对队列中所有的位置点找到距离为1的位置并继续存放在队列中,每一个点查询过后便移出。队列中没有位置点时,说明矩阵的所有位置都查询完,算法也就停止了。
代码
class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
int line = matrix.size(), row = matrix[0].size();
vector<vector<int>> dist(line, vector<int>(row));
queue<pair<int, int>> deal;
for(int i = 0; i < line; ++i){
for(int j = 0; j < row; ++j){
dist[i][j] = 0;
if(matrix[i][j] == 0){
deal.push(pair<int,int>(i, j));
}
}
}
while(!deal.empty()){
int i = deal.front().first, j = deal.front().second;
deal.pop();
// 向上
if(i>0 && matrix[i-1][j] == 1 && dist[i-1][j] == 0) {
dist[i-1][j] = dist[i][j]+1;
deal.push(pair<int, int>(i-1, j));
}
// 向下
if(i+1<line && matrix[i+1][j] == 1 && dist[i+1][j] == 0){
dist[i+1][j] = dist[i][j]+1;
deal.push(pair<int, int>(i+1, j));
}
// 向左
if(j>0 && matrix[i][j-1] == 1 && dist[i][j-1] == 0) {
dist[i][j-1] = dist[i][j]+1;
deal.push(pair<int, int>(i, j-1));
}
// 向右
if(j+1<row && matrix[i][j+1] == 1 && dist[i][j+1] == 0){
dist[i][j+1] = dist[i][j]+1;
deal.push(pair<int, int>(i, j+1));
}
}
return dist;
}
};
方法二:动态规划
解题思路
与广度优先搜索同样的思路,当位置点为0时,最小距离为0,当位置点为1时,显然其最小距离是由周边的点的距离决定的,符合归纳法的特征,就可以考虑使用动态规划算法。
动态规划是一种决策算法,在矩阵问题中,问题的本质就是从任意一个起点开始,如何行走到达某终点的步数最小,对于一个点1和点0,其路径最短的走法一定是水平向不回头走若干步,竖直方向不回头走若干步,也就是一共有四种走法:先左后上、先右后上、先左后下、先右后下,最大不超过line+row
我们思考这样几个问题:
-
一个01矩阵,左上角是0,其他位置不定,可以从任意0为起点出发,向右或向下走到达1,那么对于每一个位置为1的点,最短路径是多少?
-
一个01矩阵,右上角是0,其他位置不定,可以从任意0为起点出发,向左或向下走到达1,那么对于每一个位置为1的点,最短路径是多少?
-
一个01矩阵,左下角是0,其他位置不定,可以从任意0为起点出发,向右或向上走到达1,那么对于每一个位置为1的点,最短路径是多少?
-
一个01矩阵,右下角是0,其他位置不定,可以从任意0为起点出发,向左或向上走到达1,那么对于每一个位置为1的点,最短路径是多少?
可以发现,最终的问题变成,选择哪种走法可以使得距离最小呢?
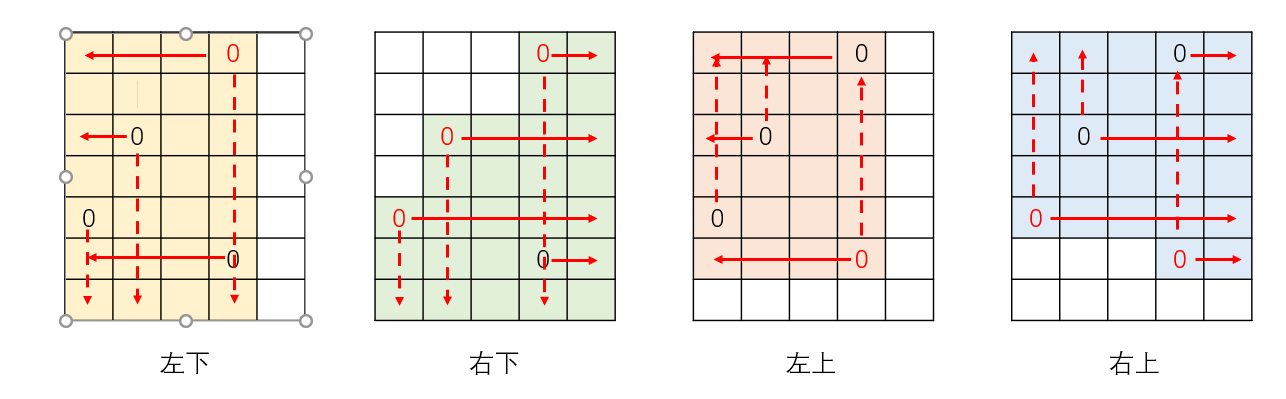
对于每一种走法,都可以进行一次搜索,每一次搜索都可能会有无法搜索到的部分(白色方格),此时我们视为无法走到,也就是距离超出最远为line+row+1,四个走法得到的距离中的最小值就是最终的结果。
在以从0到1只可以先左后上为例,初始状态为位置为0的点距离为0,决策是选择向左或者向上走,状态转移方程是
f[i][j] = matrix[i][j] * min{f[i+1][j]+1, f[i][j+1]+1}
代码
class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
int line = matrix.size(), row = matrix[0].size();
vector<vector<int>> dist(line, vector<int>(row,line+row+1));
for(int i = 0; i < line; ++i){
for(int j = 0; j < row; ++j){
if(matrix[i][j] == 0){
dist[i][j] = 0;
}
}
}
for(int i = 0; i < line; ++i){
for(int j = 0; j < row; ++j){
if(i>0) dist[i][j] = dist[i][j] < matrix[i][j]*(dist[i-1][j]+1) ? dist[i][j] : matrix[i][j]*(dist[i-1][j]+1);
if(j>0) dist[i][j] = dist[i][j] < matrix[i][j]*(dist[i][j-1]+1) ? dist[i][j] : matrix[i][j]*(dist[i][j-1]+1);
}
}
for(int i = line-1; i >= 0; --i){
for(int j = 0; j < row; ++j){
if(i<line-1) dist[i][j] = dist[i][j] < matrix[i][j]*(dist[i+1][j]+1) ? dist[i][j] : matrix[i][j]*(dist[i+1][j]+1);
if(j>0) dist[i][j] = dist[i][j] < matrix[i][j]*(dist[i][j-1]+1) ? dist[i][j] : matrix[i][j]*(dist[i][j-1]+1);
}
}
for(int i = 0; i < line; ++i){
for(int j = row-1; j >= 0; --j){
if(i>0) dist[i][j] = dist[i][j] < matrix[i][j]*(dist[i-1][j]+1) ? dist[i][j] : matrix[i][j]*(dist[i-1][j]+1);
if(j<row-1) dist[i][j] = dist[i][j] < matrix[i][j]*(dist[i][j+1]+1) ? dist[i][j] : matrix[i][j]*(dist[i][j+1]+1);
}
}
for(int i = line-1; i >= 0; --i){
for(int j = row-1; j >= 0; --j){
if(i<line-1) dist[i][j] = dist[i][j] < matrix[i][j]*(dist[i+1][j]+1) ? dist[i][j] : matrix[i][j]*(dist[i+1][j]+1);
if(j<row-1) dist[i][j] = dist[i][j] < matrix[i][j]*(dist[i][j+1]+1) ? dist[i][j] : matrix[i][j]*(dist[i][j+1]+1);
}
}
return dist;
}
};
总结
-
在广度优先搜索的写法里面,可以用一个
dirs[4][2]={{-1,0},{1,0},{0,-1},{0,1}}来记录上下左右的方向,但是这样写的问题在于每次都要进行一些重复的判断,代码整体运算速度会降低(比如如果是向下移动,只需要判断line是否小于最大行数,而不用判断大于0,但是如果用dirs就要重复判断了) -
对于动态规划算法,可以只搜索左上和右下两种走法也可以得到最终结果,因为对于搜索完左上的矩阵,已经保存了向左和向上的路线信息了,搜索右时可以得到右上信息,搜索下时也可以得到左上信息。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号