算法分析(4)-排序-归并排序
1简单释义
less和exch可以查看上一章:算法分析(3)-简单排序总结(选择,插入,希尔含图解)——Comparable接口
归并采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。归并排序是一种稳定的排序方法。
- 归并排序能够保证将任意长度为$N$的数组排序所需时间和$NlogN$成正比;
- 归并排序的主要缺点是其所需的额外空间与$N$成正比。
2 自顶向下的归并排序
2.1图解
自顶向下其实是先完成左侧数组然后完成右侧数组的排序规则:
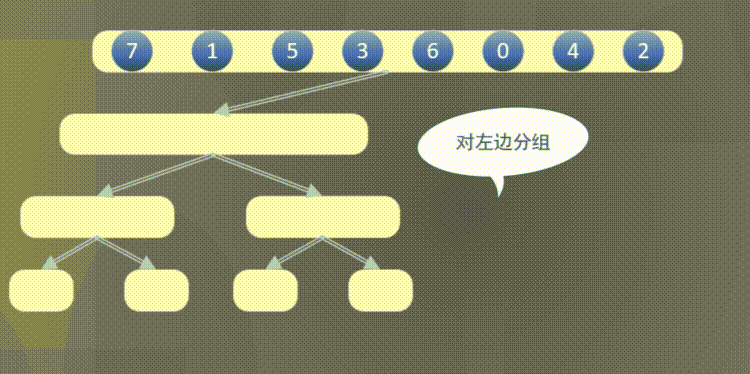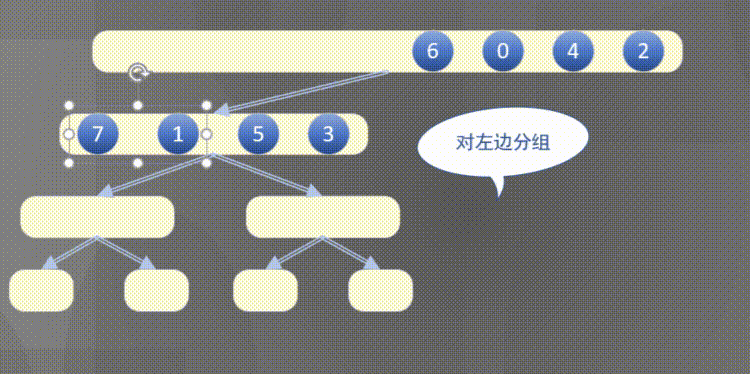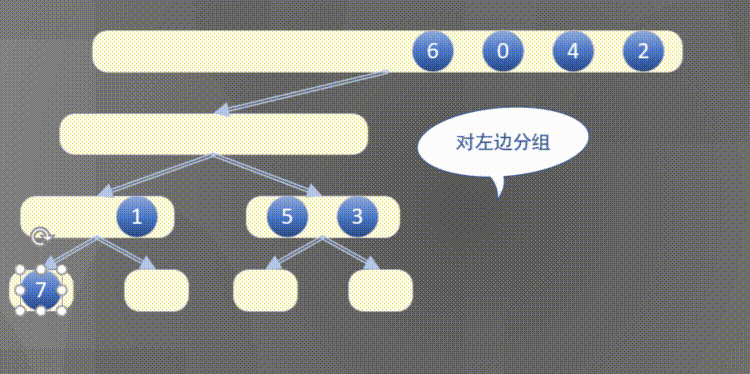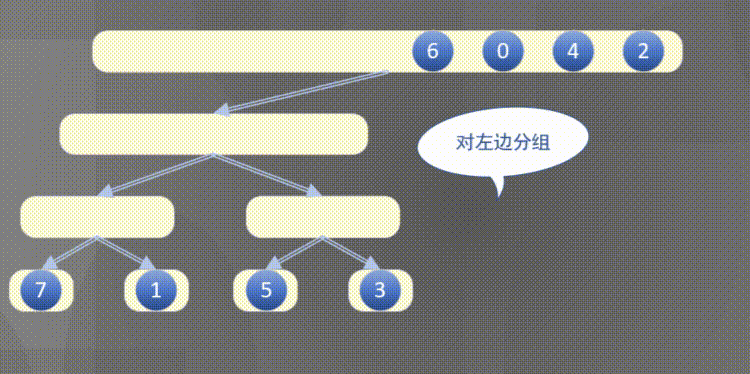
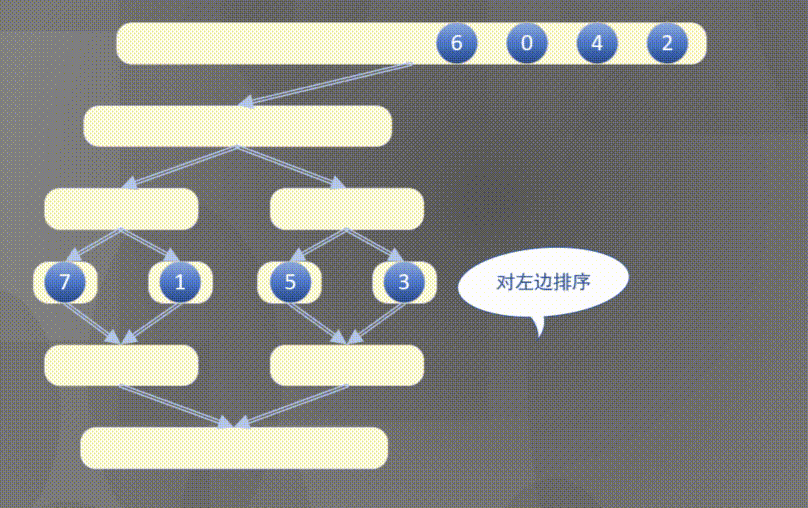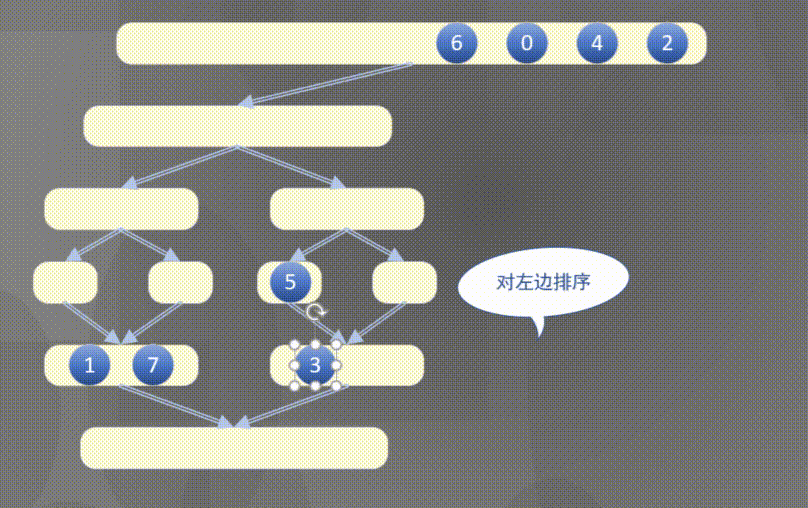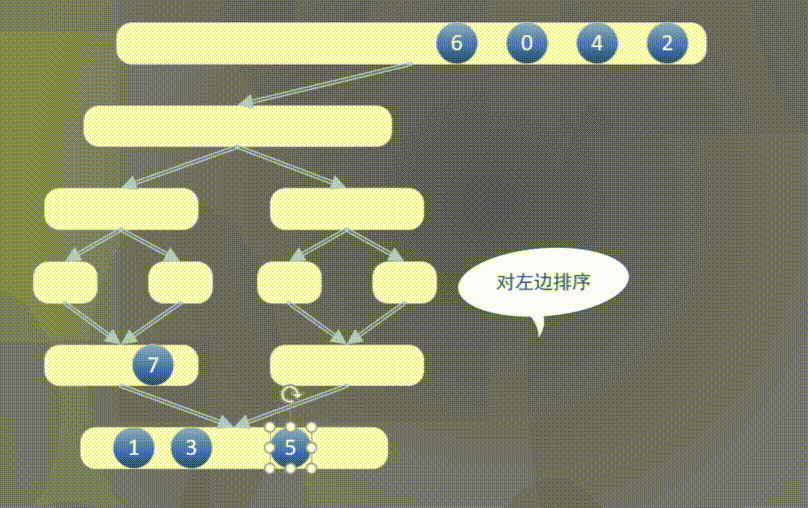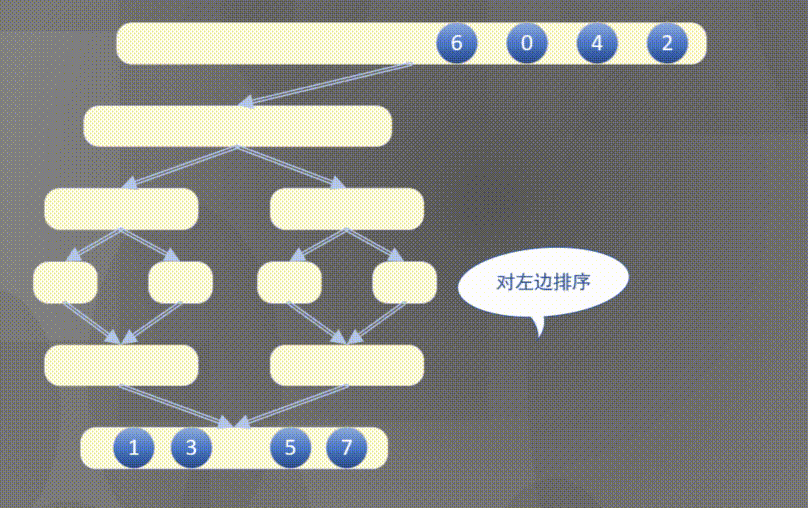
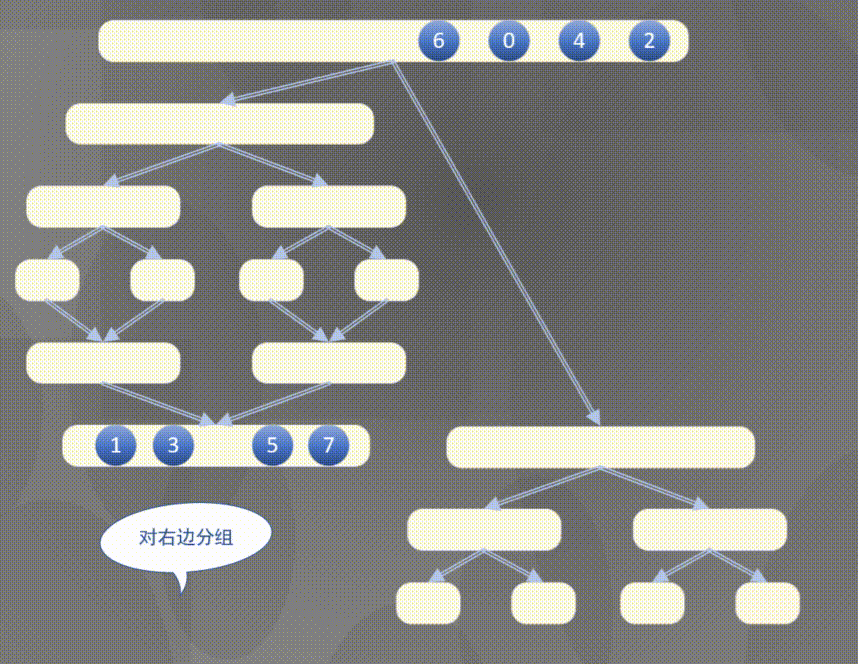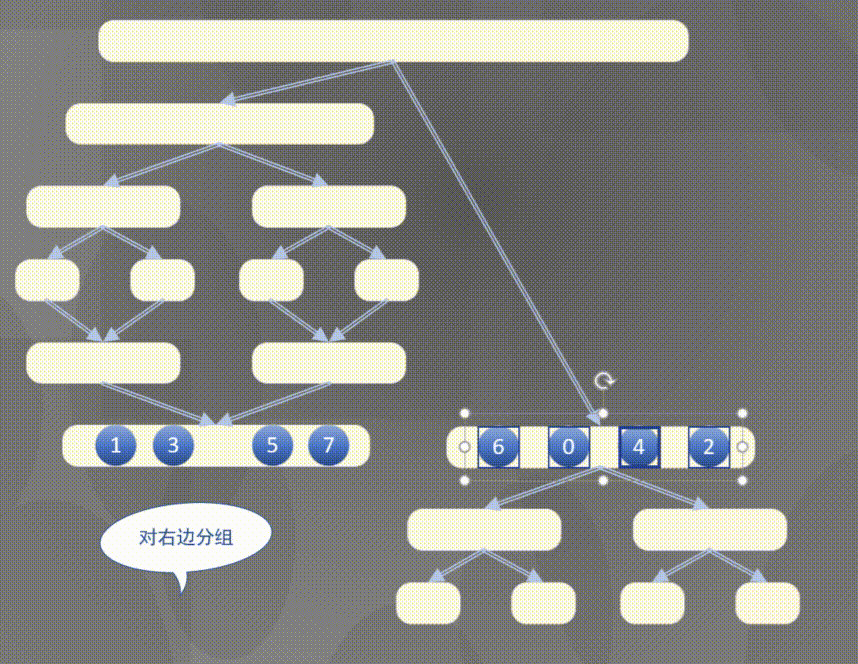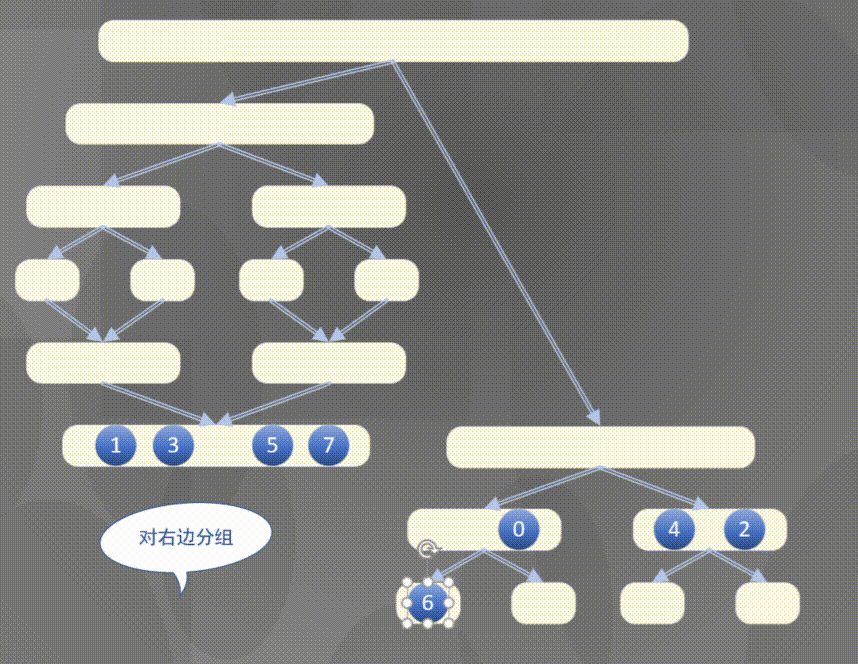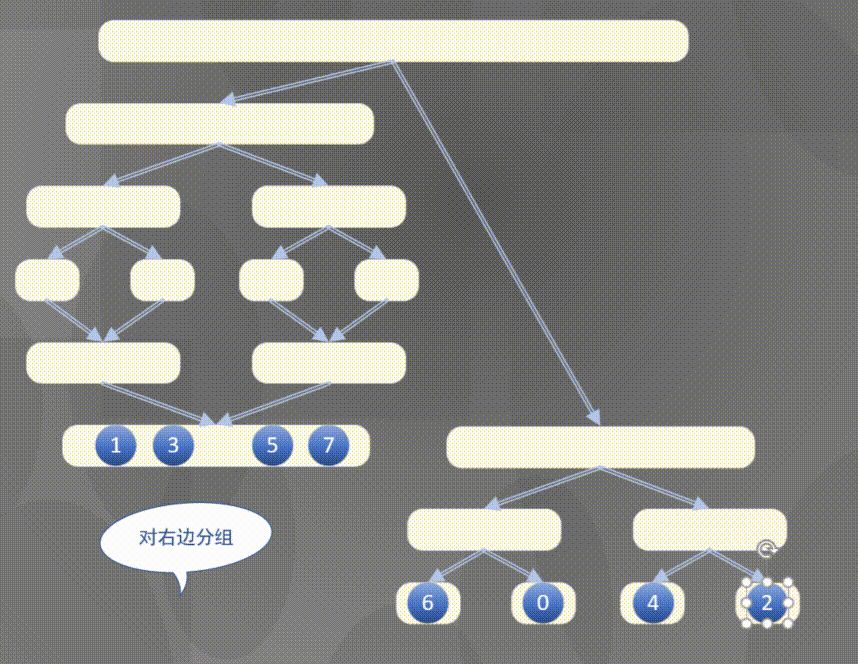
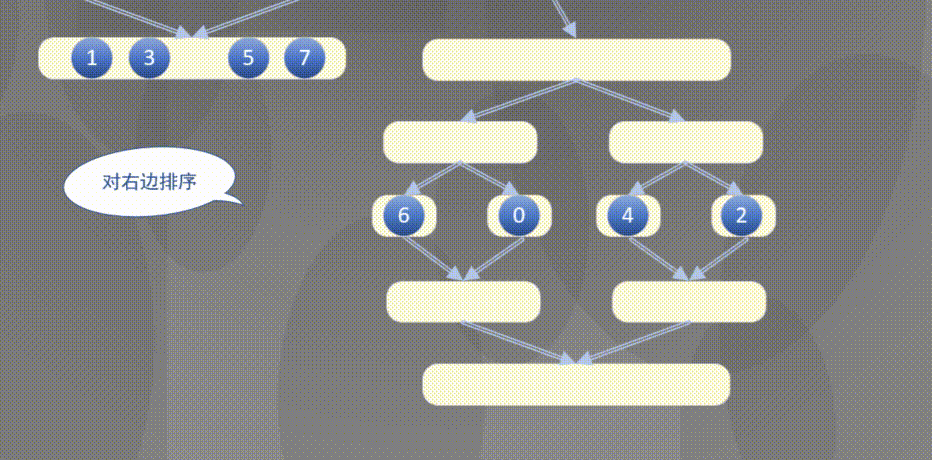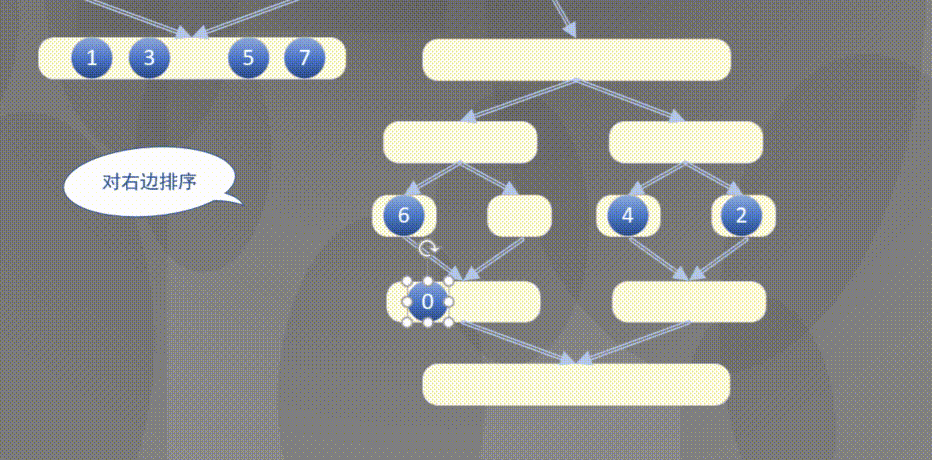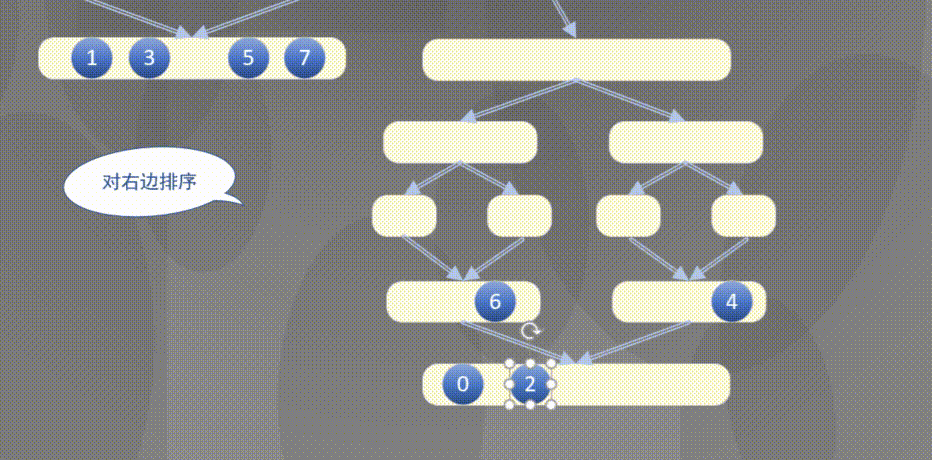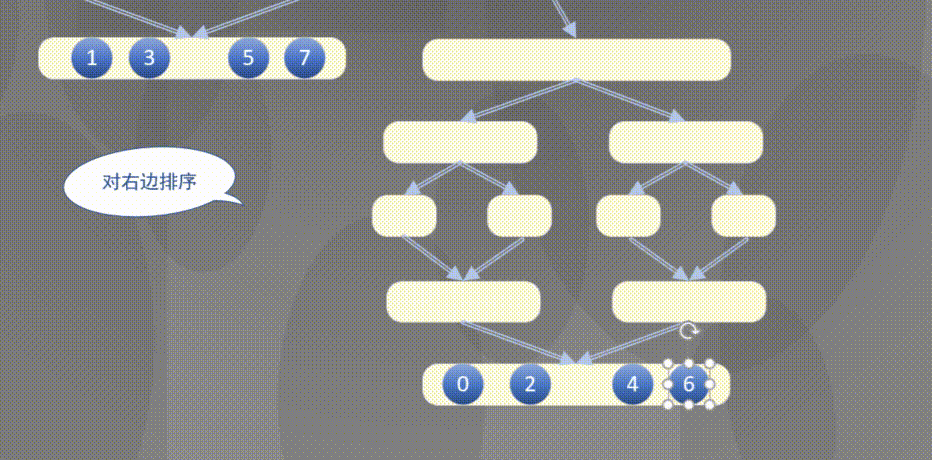
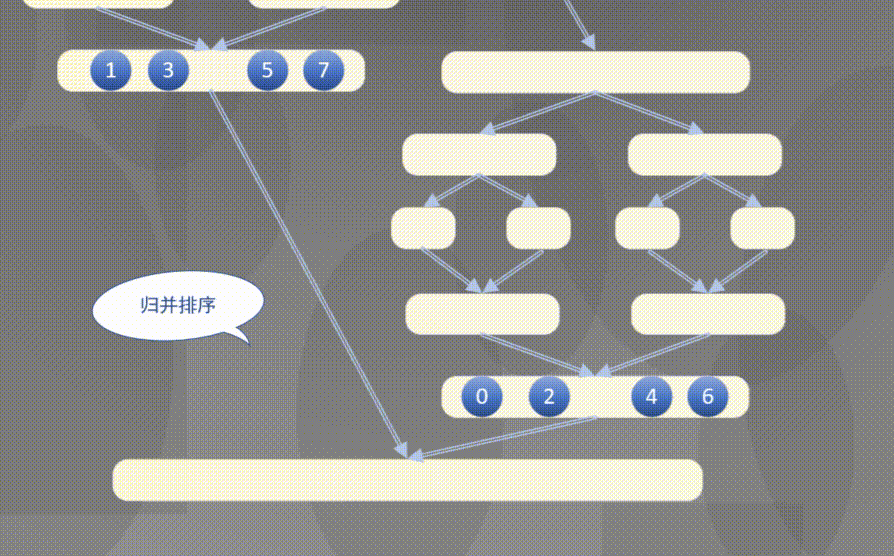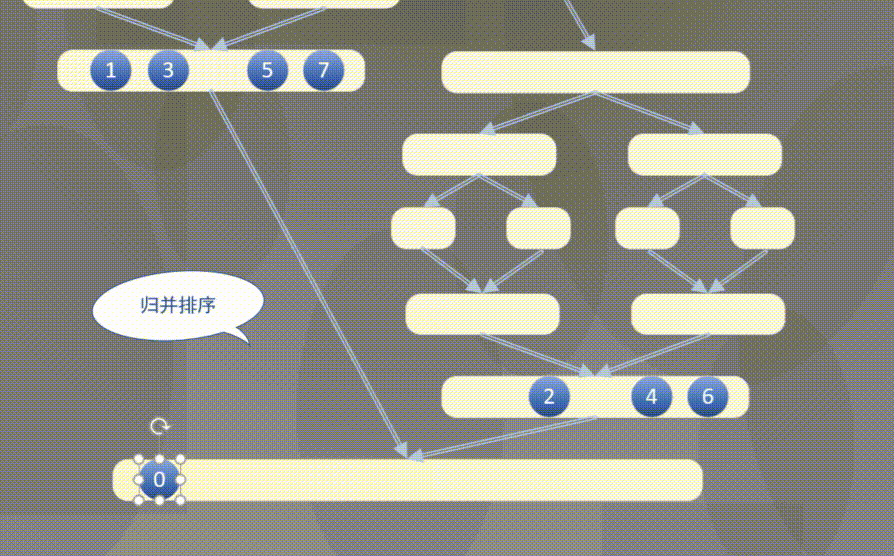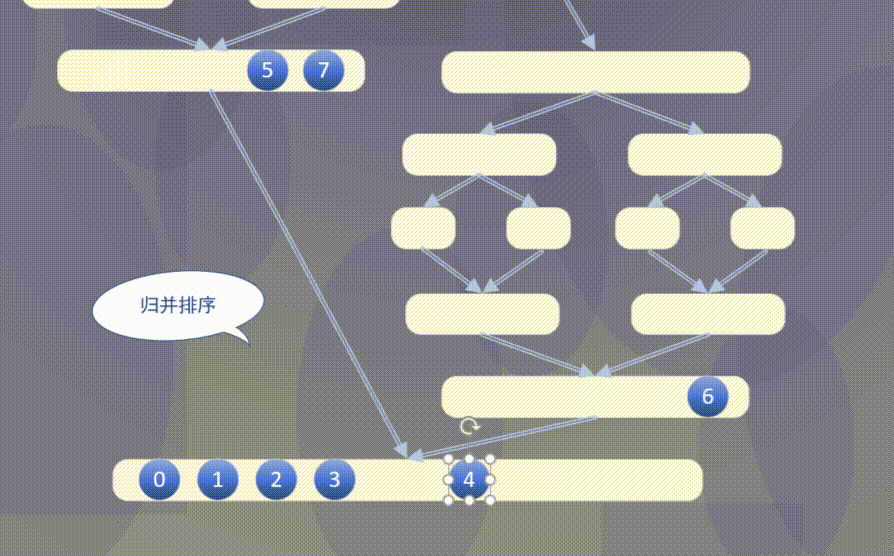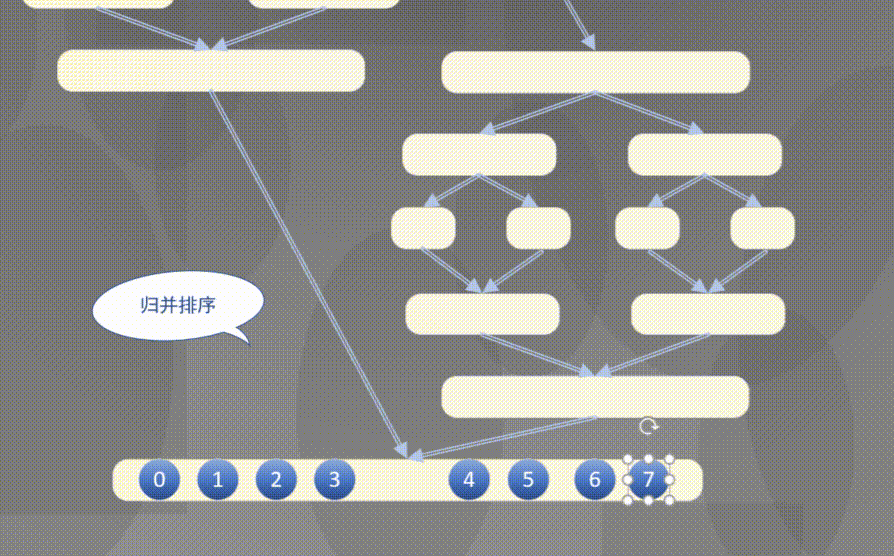
2.2 原地归并抽象方法的解释
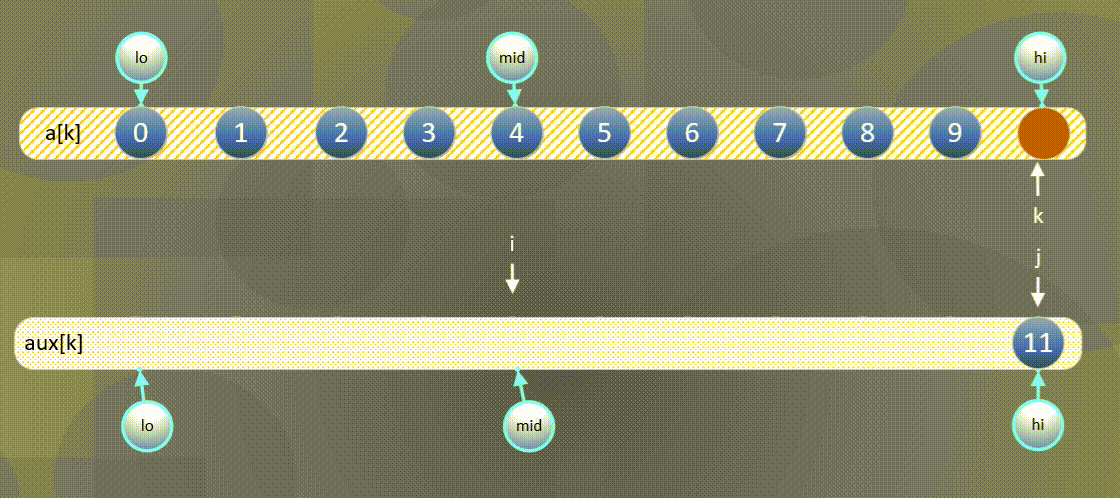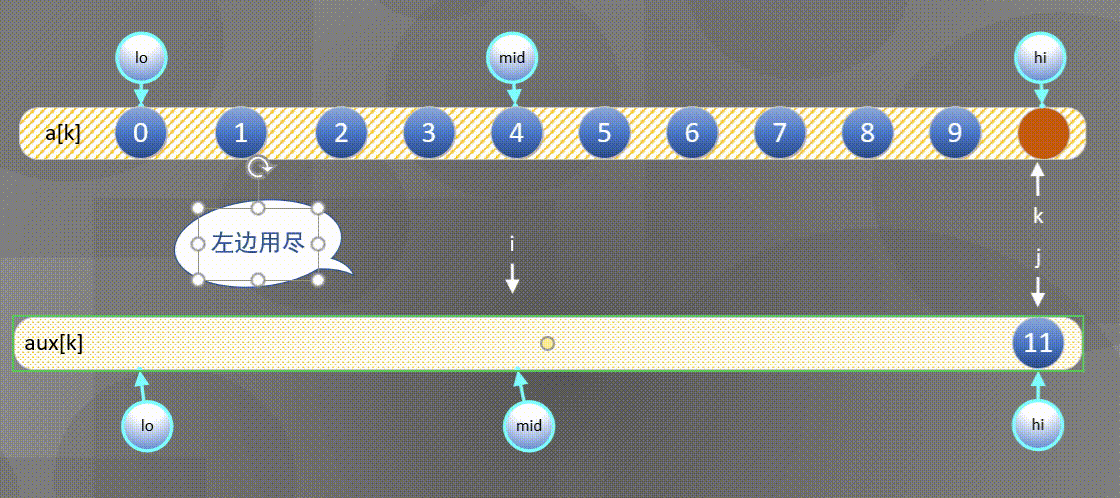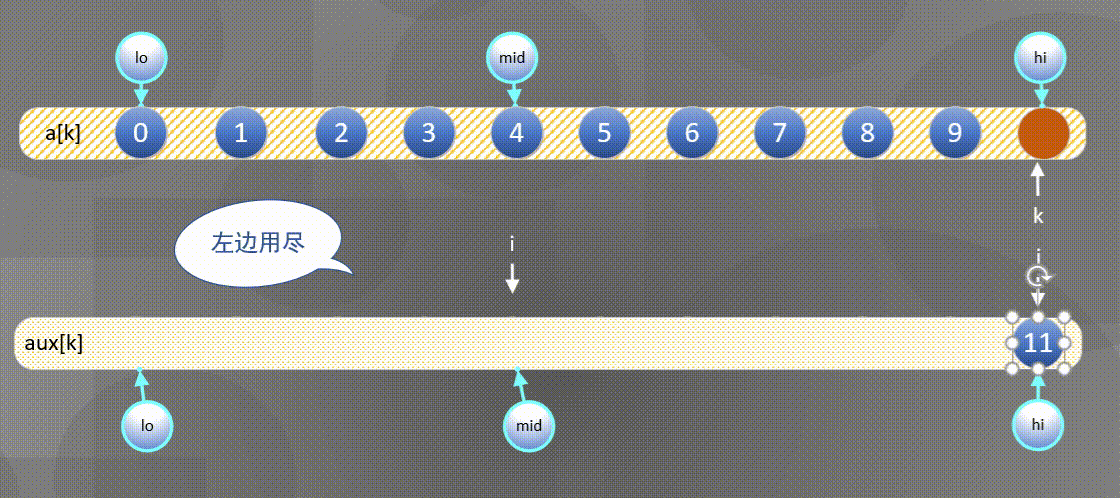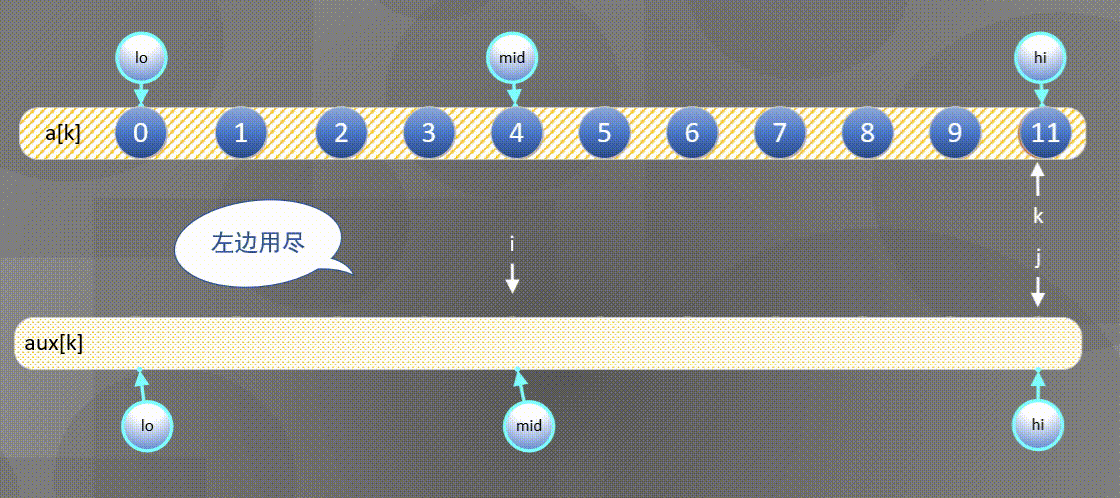
实现归并的一种方式就是直接将两个有序数组归并到第三个数组中,图示如下:
- 首先将左右序列排序好的数组$a[k]$所有元素复制到$aux[k]$中:
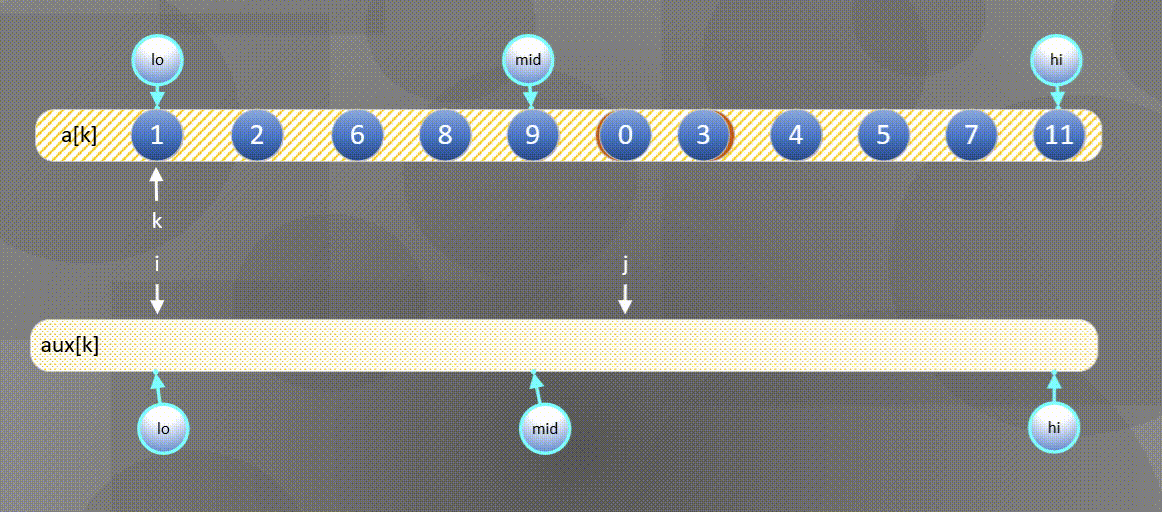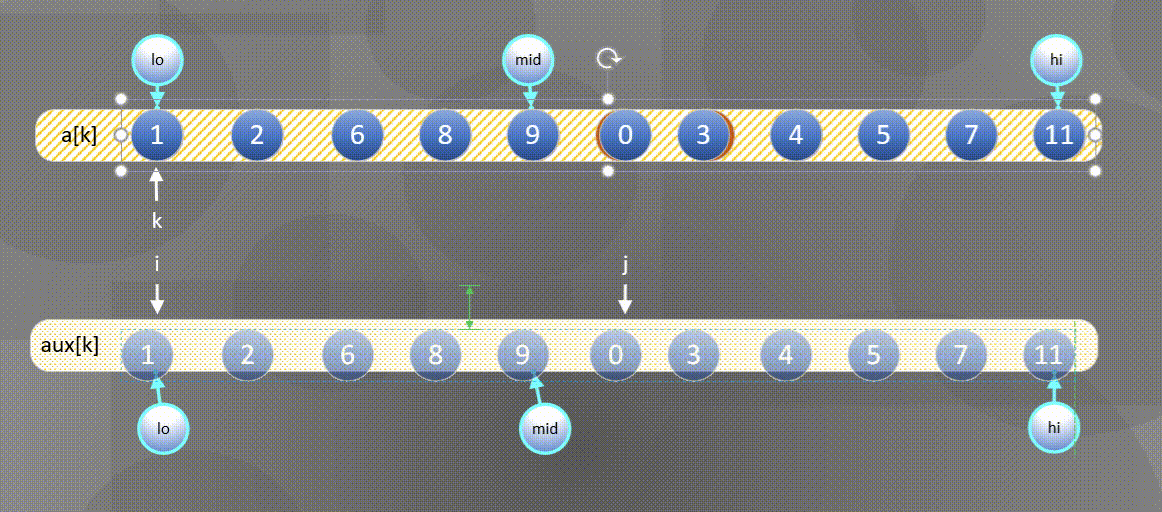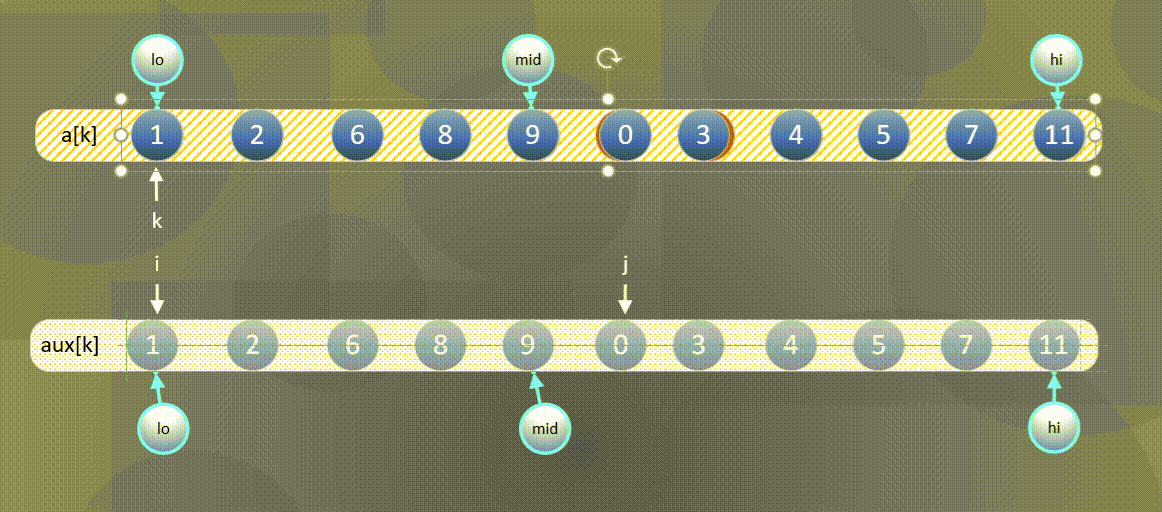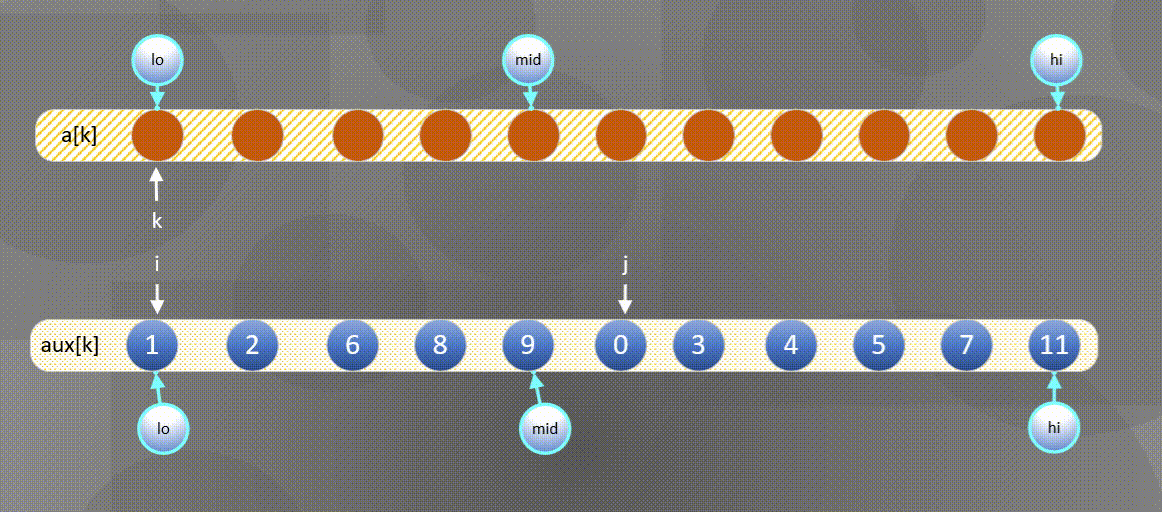
2. 然后将$aux[k]$中的元素归并到$a[k]$中。
- 如果右方元素较小将$aux[j]$中的元素归并到$a[k]$中,
- 如果左方元素较小将$aux[i]$中的元素归并到$a[k]$中。
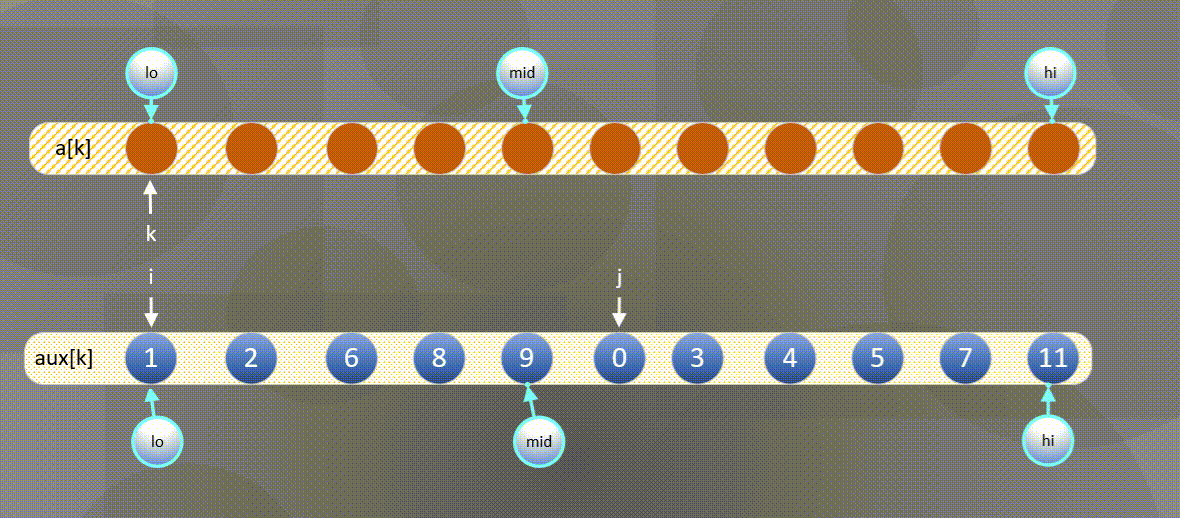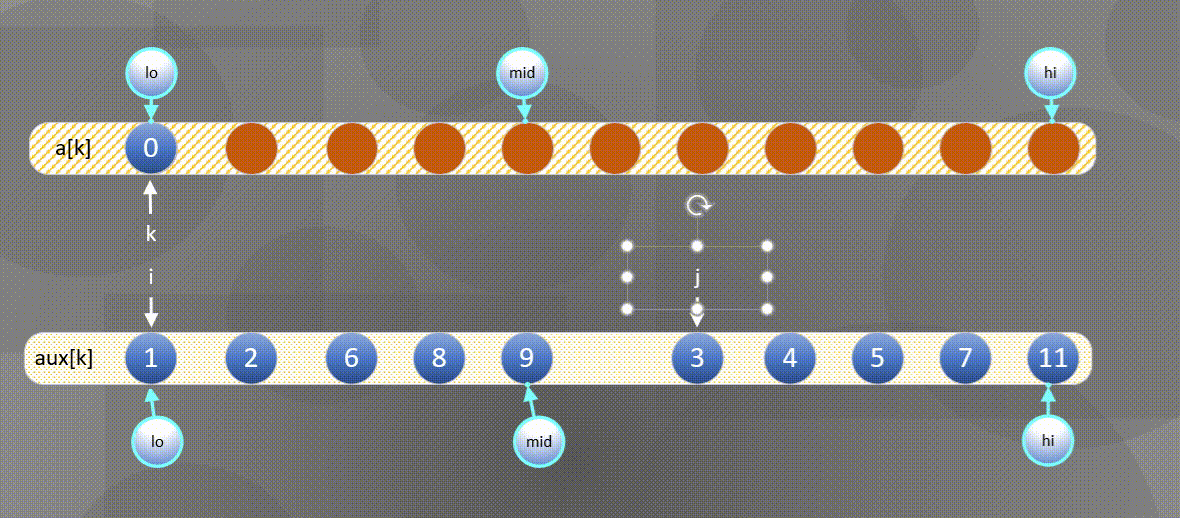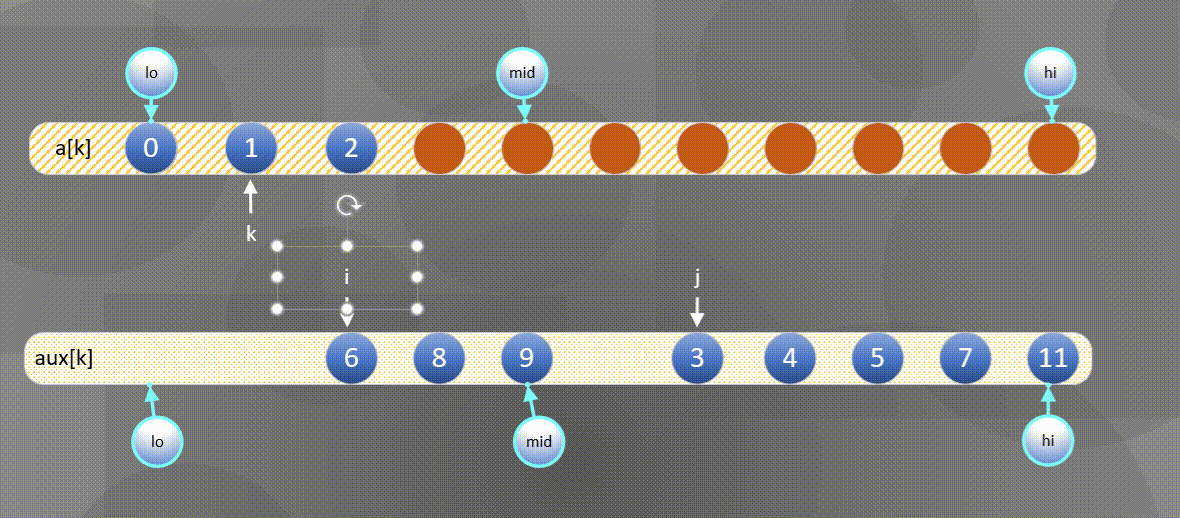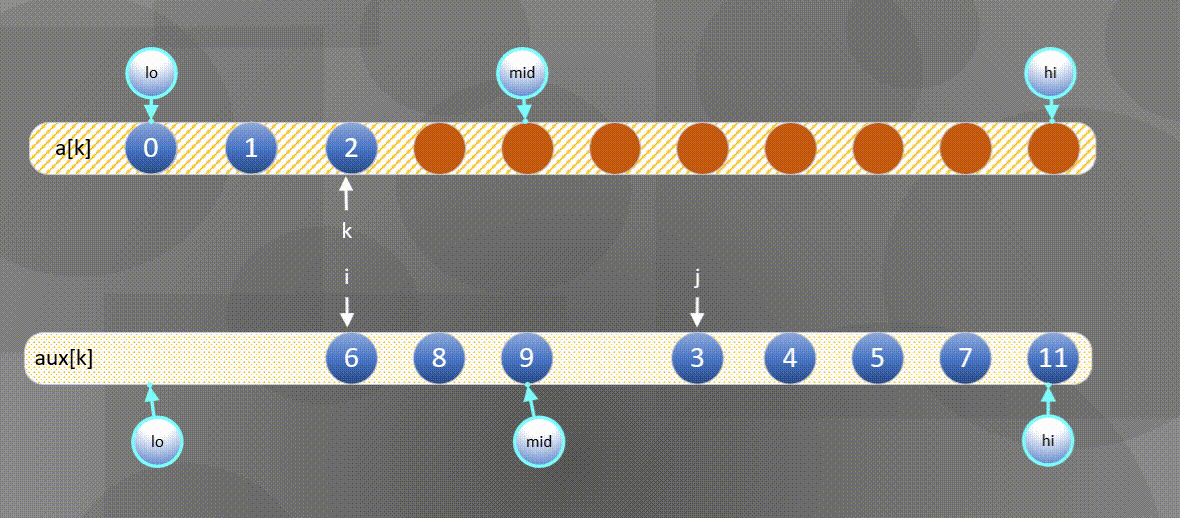
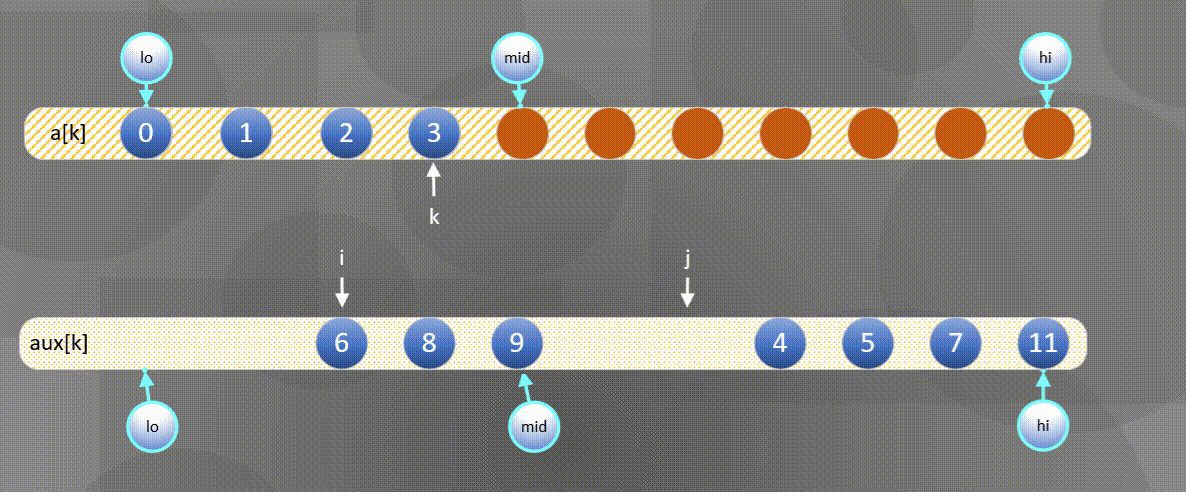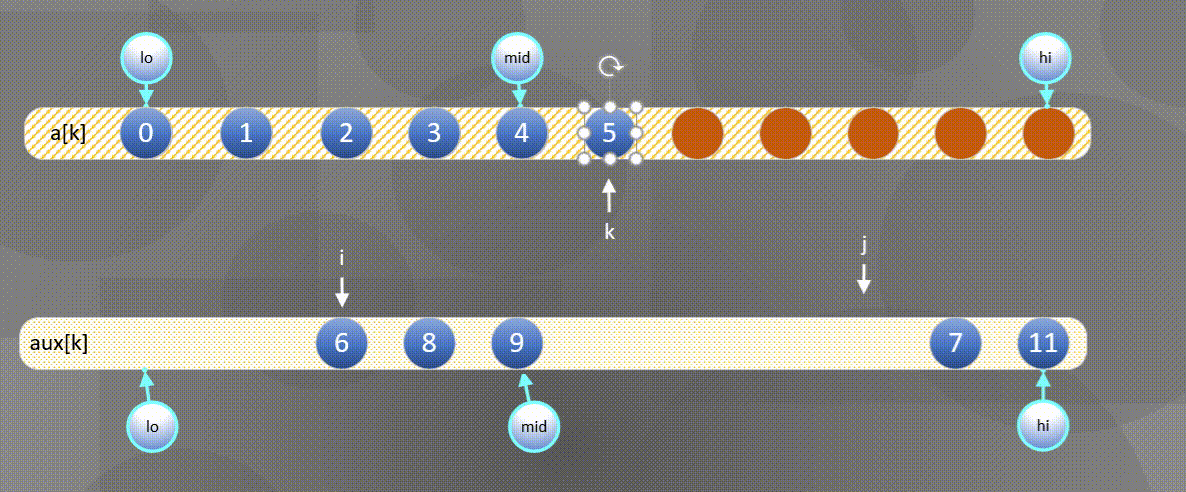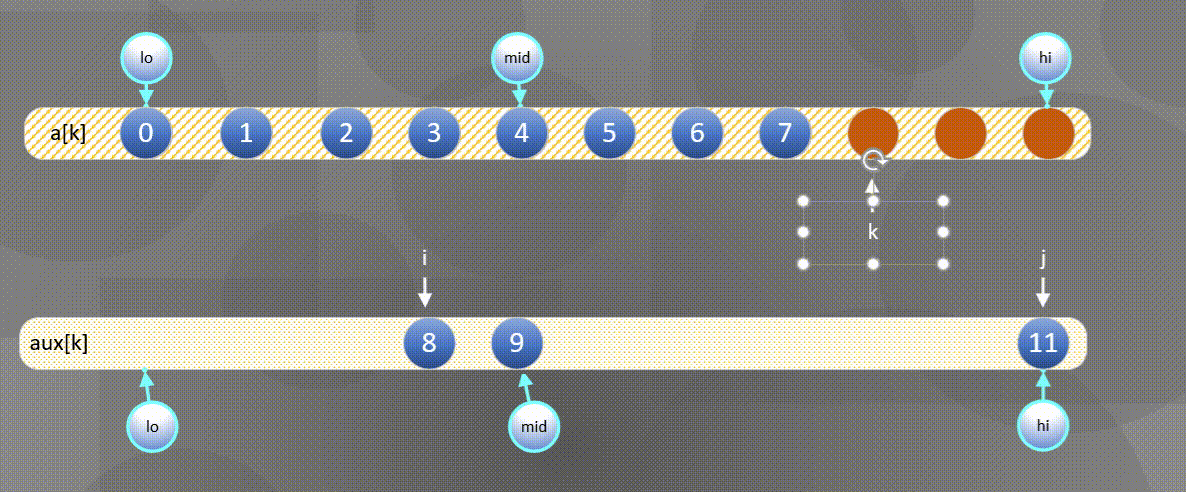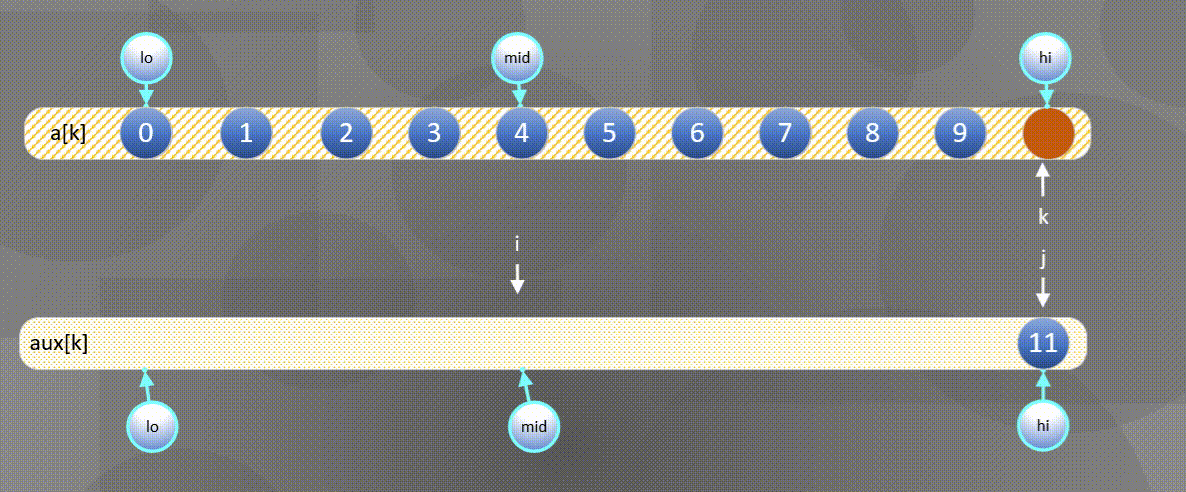
左边用尽直接将后半部分$aux[j]$复制到$a[k]$
原地归并算法如下:
这里的$less$可以查看上一章算法分析(3)-简单排序总结(选择,插入,希尔含图解)
//lo第一个元素,hi最后一个元素
private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi)
{
for (int k = lo; k <= hi; k++)
aux[k] = a[k];
int i = lo, j = mid+1;
for (int k = lo; k <= hi; k++)
{
if (i > mid) a[k] = aux[j++];//左边用尽直接将后半部分复制到a[k]
else if (j > hi) a[k] = aux[i++];//右边用尽直接将前半部分复制到a[k]
else if (less(aux[j], aux[i])) a[k] = aux[j++];//右方元素较小,复制到a[k],
else a[k] = aux[i++];//左方元素较小,复杂到a[k]
}
}
使用以上的抽象方法可以使用递归的方式完成递归排序。
2.3自顶向下的归并排序
首先上代码:
//递归的实现归并排序
public class Merge {
private static Comparable[] aux;//归并所需的辅助数组
public class void sort(Comparable[] a)
{
aux=new Comparable[a.length];//为辅助数组分配空间
sort(a,0,a.length-1);//递归过程
}
//排序
private static void sort(Comparable[] a, int lo, int hi) {
if (hi <= lo) return;
int mid = lo + (hi - lo) / 2;
sort(a,lo, mid);//排序左侧
sort(a,mid + 1, hi);//排序右侧
merge(a,lo, mid, hi);//归并过程,见上方抽象方法说明
}
}
其实$sort$的的作用只是对$merge$执行的顺序完成合理调用。
这里直接给出对于长度为$N$的数组,自顶向下的归并排序的比较次数:$1/2NlgN$~$NlgN$
访问数组的次数(最多):$6NlgN$
关于算法规模的计算以及数学分析的相关证明,会在本专栏之后进行更新。
2.4自顶向下的归并排序优化建议
代码后期会在github上更新,目前博主的git在商用,暂时不放优化代码
- 对小规模子数组使用插入排序
- 对子数组随时检测是否有序
- 不讲元素复制到辅助数组
3 自底向上的归并排序
3.1图解
自底向上其实就是从所有数组中最小分组进行归并排序
首先进行分解(这里的分解其实使用递归即可):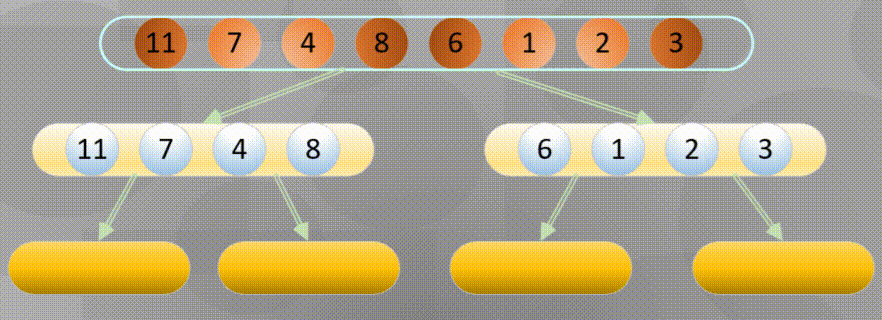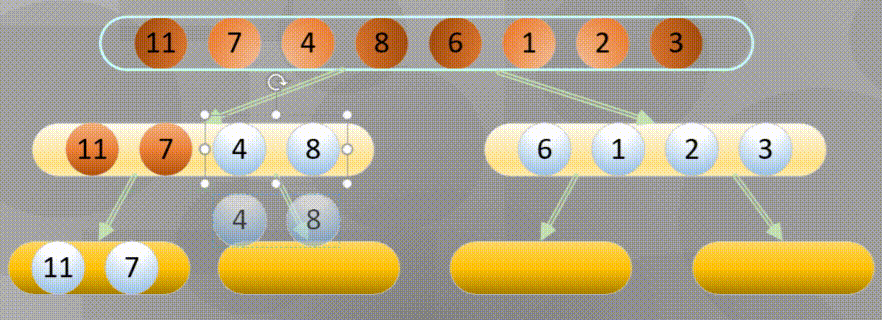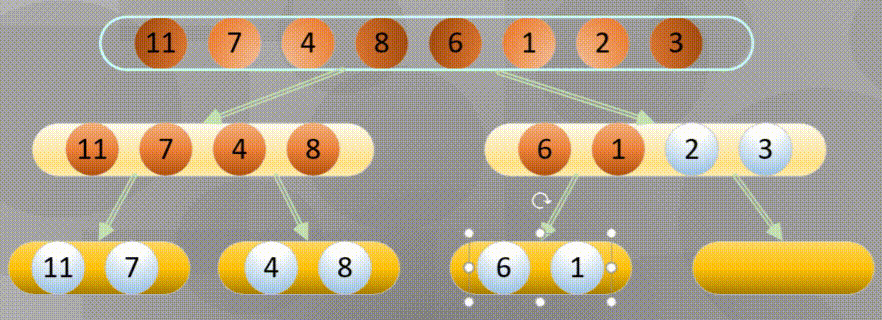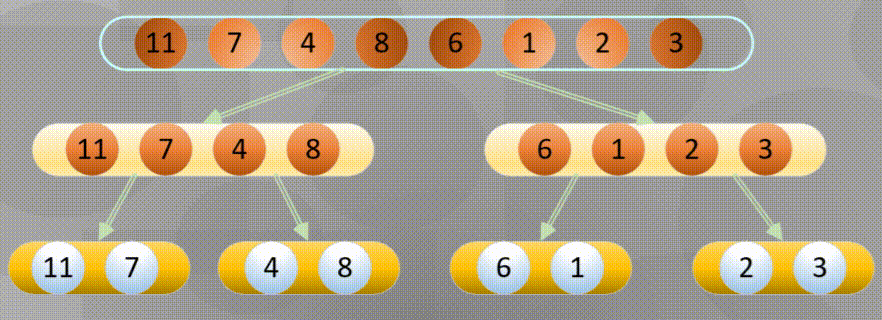
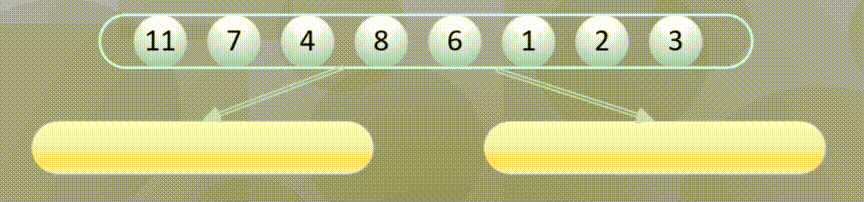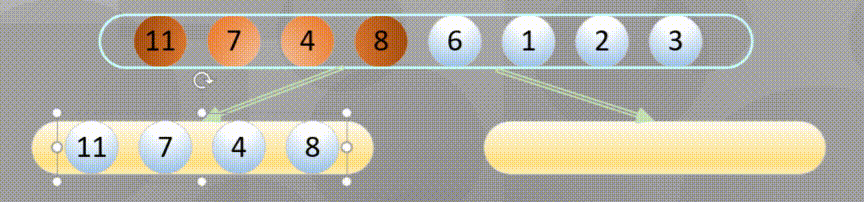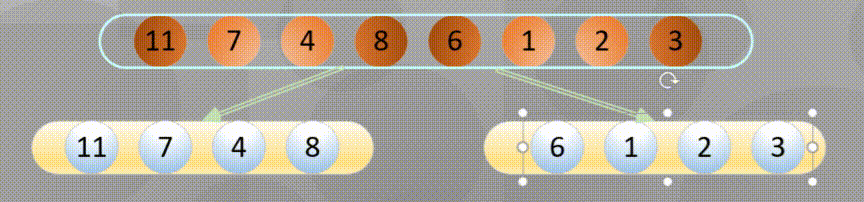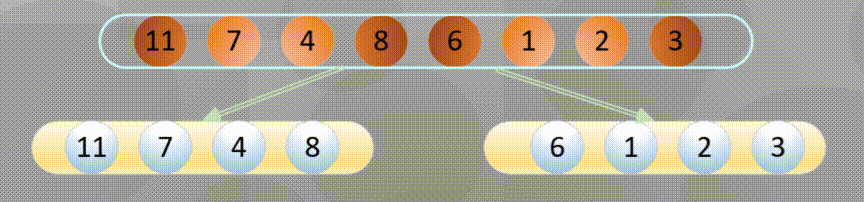
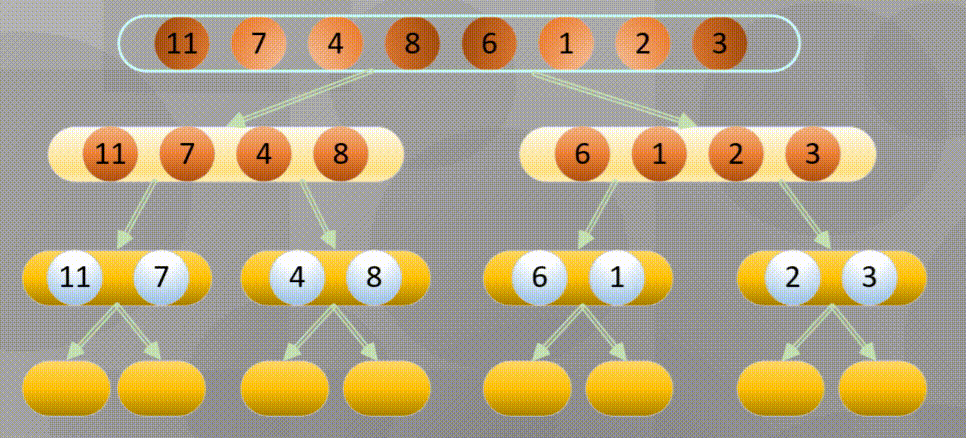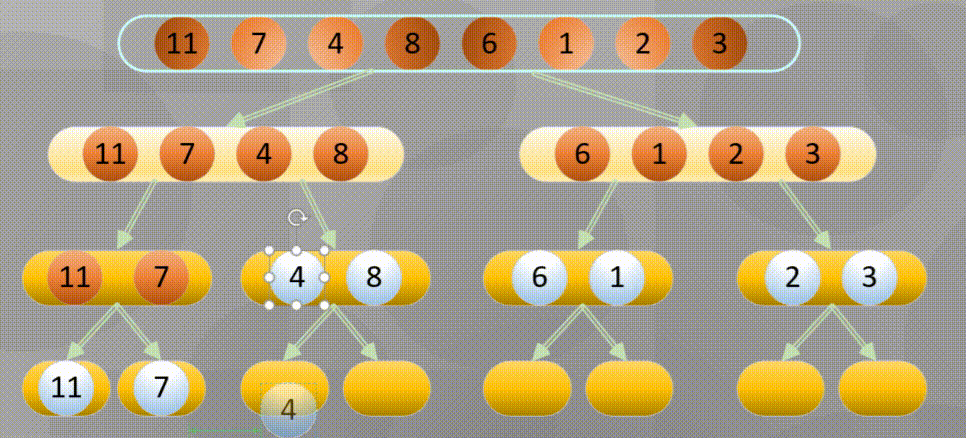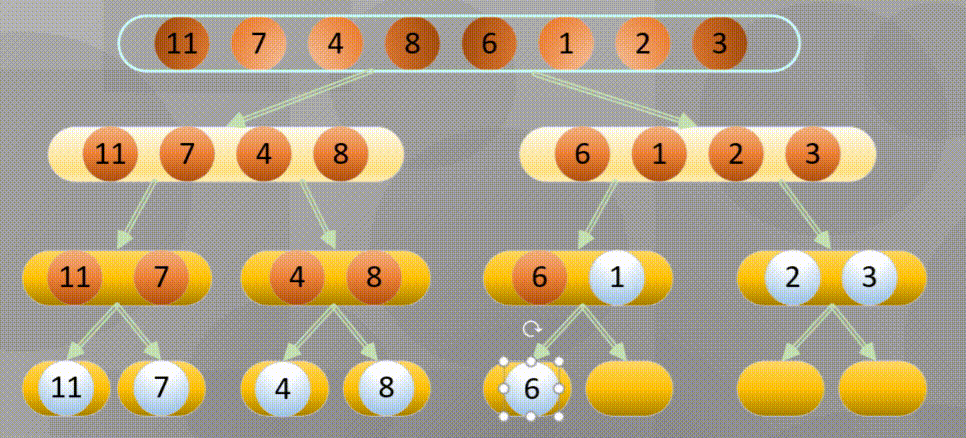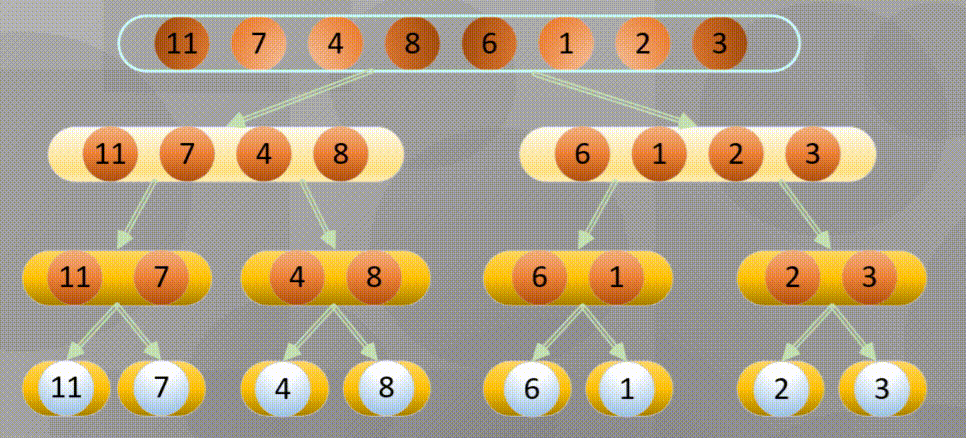
当分解到最简元素时进行原地归并:

3.2代码
//递归的实现归并排序
public class Merge {
private static Comparable[] aux;//归并所需的辅助数组
public static void sort(Comparable[] a)
{
int N=a.length;
aux=new Comparable[N];//为辅助数组分配空间
for(int sz=1;sz<N;sz=sz+sz)
for(int lo=0;lo<N-sz;lo+=sz+sz)
merge(a.lo.lo+sz-1;Math.min(lo+sz+sz-1,N-1));//见上方抽象方法说明
}
}
这里直接给出对于长度为$N$的数组,自顶向下的归并排序的比较次数:$1/2NlgN$~$NlgN$
访问数组的次数(最多):$6NlgN$

