算法金 | 一个强大的算法模型,GPR !!

大侠幸会,在下全网同名「算法金」 0 基础转 AI 上岸,多个算法赛 Top 「日更万日,让更多人享受智能乐趣」
高斯过程回归(GPR)是一种非参数化的贝叶斯方法,用于解决回归问题。与传统的线性回归模型不同,GPR 能够通过指定的核函数捕捉复杂的非线性关系,并提供不确定性的估计。在本文中,我们将详细介绍 GPR 算法的定义、核心思想和数学基础,并通过实例展示其在实际应用中的效果。
GPR 算法简介
GPR 的定义
高斯过程回归(Gaussian Process Regression, GPR)是一种基于高斯过程的统计模型,用于处理回归问题。高斯过程是一种分布,每个样本点都遵循一个高斯分布,这使得 GPR 在处理数据的非线性关系时表现出色。GPR 的核心是利用高斯过程的性质,通过指定合适的核函数,对数据进行建模和预测。
核心思想和原理
GPR 的核心思想是通过高斯过程来描述输入数据的潜在函数,即假设数据来自一个多变量正态分布。核函数是 GPR 的关键,它决定了模型的平滑度、周期性等特性。常用的核函数包括径向基函数(RBF)、线性核函数等。
在 GPR 模型中,通过高斯过程的协方差矩阵来描述样本点之间的关系,进而对未知数据点进行预测。
GPR 算法的数学基础
高斯过程回归的数学模型
高斯过程回归(GPR)的数学模型可以通过以下步骤来描述:
- 定义高斯过程:高斯过程是一个由多变量正态分布定义的随机过程。

- 核函数的定义:核函数(也称为协方差函数)用于衡量输入点之间的相关性。常用的核函数包括径向基函数(RBF)、线性核函数等。例如,RBF 核函数的形式为:
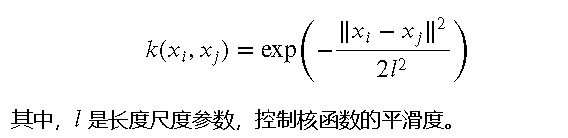

核函数及其作用
核函数是 GPR 的核心,它决定了模型的平滑度、周期性等特性。选择合适的核函数可以显著提高模型的性能。常见的核函数包括:
- 径向基函数(RBF)核:适用于平滑且连续的函数建模。
- 线性核:适用于线性关系建模。
- 周期核:适用于周期性数据建模。
核函数的形式和参数需要根据具体问题进行选择和调整。
超参数选择与优化
GPR 模型的超参数包括核函数的参数和噪声项。超参数选择通常通过最大化对数似然函数来实现。对数似然函数的形式为:
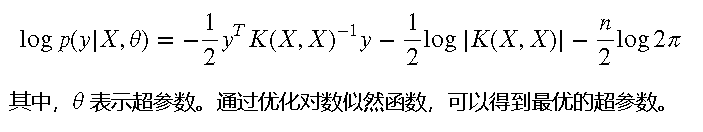
防失联,进免费知识星球,直达算法金 AI 实验室 https://t.zsxq.com/ckSu3
GPR 算法的实现与应用
import numpy as np
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, ConstantKernel as C
import matplotlib.pyplot as plt
# 武林大会随机种子
np.random.seed(1)
# 生成模拟数据
X = np.random.uniform(0, 5, (1000, 3)) # 特征数据,代表武林中高手的内功心法参数
y = np.sin(X[:,0]) + np.cos(X[:,1]) + 0.1 * np.random.randn(1000) # 目标数据,代表不同门派的武学修为
# 定义核函数,仿佛内功的核心修炼方法
kernel = C(1.0, (1e-3, 1e3)) * RBF(1.0, (1e-2, 1e2))
# 创建高斯过程回归模型,就如同一个武学大师
gpr = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=9)
# 训练模型,犹如将不同门派的武功秘籍尽收囊中
gpr.fit(X, y)
# 生成测试数据集,确保总数是3的倍数,如同江湖中三大门派的比武招亲
X_test = np.linspace(0, 5, 99).reshape(-1, 3)
y_pred, sigma = gpr.predict(X_test, return_std=True)
# 绘图,如同在武林大会上展示各派武学的威力
plt.figure()
plt.plot(X[:,0], y, 'r.', markersize=10, label='江湖中的高手')
plt.plot(X_test[:,0], y_pred, 'b-', label='武学预测')
plt.fill(np.concatenate([X_test[:,0], X_test[:,0][::-1]]),
np.concatenate([y_pred - 1.9600 * sigma, (y_pred + 1.9600 * sigma)[::-1]]),
alpha=.5, fc='b', ec='None', label='95% 置信区间')
plt.xlabel('内功心法参数')
plt.ylabel('武学修为')
plt.legend(loc='upper left')
# 展现武林大会上的巅峰对决
plt.show()
我们来一步一步解读这段代码
import numpy as np
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, ConstantKernel as C
import matplotlib.pyplot as plt
首先,我们导入必要的库:
- numpy 用于数值计算。
- sklearn 中的 GaussianProcessRegressor 和核函数,用于构建和训练高斯过程回归模型。
- matplotlib 用于数据可视化。
# 武林大会随机种子
np.random.seed(1)
这里设置了随机种子,以确保结果的可重复性。把它比作武林大会上,确保每次比武规则一致。
# 生成模拟数据
X = np.random.uniform(0, 5, (1000, 3)) # 特征数据,代表武林中高手的内功心法参数
y = np.sin(X[:,0]) + np.cos(X[:,1]) + 0.1 * np.random.randn(1000) # 目标数据,代表不同门派的武学修为
生成特征数据 X,包含 1000 个样本,每个样本有 3 个特征,取值范围在 0 到 5 之间。这些特征可以想象成武林中高手的内功心法参数。生成目标数据 y,它是由第一个特征的正弦值和第二个特征的余弦值加上少量噪声组成的,代表不同门派的武学修为。
# 定义核函数,仿佛内功的核心修炼方法
kernel = C(1.0, (1e-3, 1e3)) * RBF(1.0, (1e-2, 1e2))
定义高斯过程回归模型的核函数,这里使用的是常数核函数 C 和径向基函数核 RBF 的乘积。核函数在这里类似于武林中不同门派的核心修炼方法,它决定了模型如何去拟合数据。
# 创建高斯过程回归模型,就如同一个武学大师
gpr = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=9)
创建一个高斯过程回归模型,这个模型就像是一个武学大师,能够吸收和理解不同门派的武学秘籍。
# 训练模型,犹如将不同门派的武功秘籍尽收囊中
gpr.fit(X, y)
训练模型,犹如这个武学大师将所有门派的武功秘籍尽收囊中,形成自己的独门绝技。
# 生成测试数据集,确保总数是3的倍数,如同江湖中三大门派的比武招亲
X_test = np.linspace(0, 5, 99).reshape(-1, 3)
y_pred, sigma = gpr.predict(X_test, return_std=True)
生成测试数据集,并进行预测。这里生成了 99 个测试样本,并确保每个样本有 3 个特征。预测结果 y_pred 和预测标准差 sigma 就像是预测每个门派弟子的武学修为及其不确定性。
# 绘图,如同在武林大会上展示各派武学的威力
plt.figure()
plt.plot(X[:,0], y, 'r.', markersize=10, label='江湖中的高手')
plt.plot(X_test[:,0], y_pred, 'b-', label='武学预测')
plt.fill(np.concatenate([X_test[:,0], X_test[:,0][::-1]]),
np.concatenate([y_pred - 1.9600 * sigma, (y_pred + 1.9600 * sigma)[::-1]]),
alpha=.5, fc='b', ec='None', label='95% 置信区间')
plt.xlabel('内功心法参数')
plt.ylabel('武学修为')
plt.legend(loc='upper left')
# 展现武林大会上的巅峰对决
plt.show()
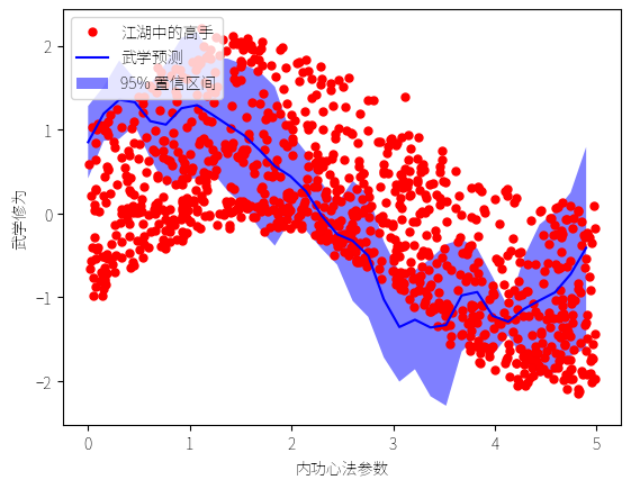
最后,我们将结果绘制出来,仿佛在武林大会上展示各派武学的威力:
- 红色点表示训练数据,即江湖中的高手们。
- 蓝色线表示预测值,即预测的武学修为。
- 蓝色阴影区域表示 95% 置信区间,展示预测的不确定性。
[ 抱个拳,总个结 ]
每天一个小案例,如果类似这样的文章对你有启发。
大侠,关注、点赞、转发走起~
- 科研为国分忧,创新与民造福 -

日更时间紧任务急,难免有疏漏之处,还请大侠海涵内容仅供学习交流之用,部分素材来自网络,侵联删
[ 算法金,碎碎念 ]
搬 砖 不 易 ~
日 更 到 哭 55



全网同名,日更万日,让更多人享受智能乐趣
如果觉得内容有价值,烦请大侠多多 分享、在看、点赞,助力算法金又猛又持久、很黄很 BL 的日更下去;同时邀请大侠 关注、星标 算法金,围观日更万日,助你功力大增、笑傲江湖



