算法金 | 必会的机器学习评估指标

大侠幸会，在下全网同名[算法金] 0 基础转 AI 上岸，多个算法赛 Top [日更万日，让更多人享受智能乐趣]

构建机器学习模型的关键步骤是检查其性能，这是通过使用验证指标来完成的。 选择正确的验证指标就像选择一副水晶球：它使我们能够以清晰的视野看到模型的性能。 在本指南中，我们将探讨分类和回归的基本指标和有效评估模型的知识。 学习何时使用每个指标、优点和缺点以及如何在 Python 中实现它们。

1 分类指标

1.1 分类结果 在深入研究分类指标之前，我们必须了解以下概念：

• 真正例 (TP)：模型正确预测正类的情况。
• 假正例 (FP)：模型预测为正类，但实际类为负类的情况。
• 真反例 (TN)：模型正确预测负类的情况。
• 假反例 (FN)：模型预测为阴性类别，但实际类别为阳性的情况。

简单来说，真正例和真反例，就像是模型正确识别出了正类与反类，而假正例和假反例。

1.2 准确度 准确率是最直接的分类指标，衡量正确预测的比例。虽然准确率易于理解和计算，但在类别不平衡的情况下，可能会产生误导。在这种情况下，考虑其他指标是至关重要的。准确率的公式为：

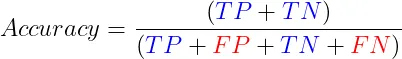
概括：

• 易于理解和沟通，并提供对模型性能的简单评估。
• 不适合不平衡的类别，因为它可能有利于多数类别。
• 无法区分假阳性和假阴性。
• 应与其他指标结合使用。

这是一种在 Python 中计算准确度得分的方法。我们可以使用以下代码将模型预测的值 ( y_pred ) 与真实值 ( y_test ) 进行比较：

from sklearn.metrics import precision_score 



# 计算模型的精确度得分

model_precision = precision_score(y_test, y_pred) 

print("Precision:", model_precision)

1.3 混淆矩阵

混淆矩阵是一个表格，总结了分类模型的表现，通过比较预测值和实际值。它为我们提供了一个模型表现的直观表示，帮助识别模型的错误之处。它显示了我们的所有四个分类结果。混淆矩阵提供了模型性能的直观表示，并有助于识别模型在哪里犯了错误。

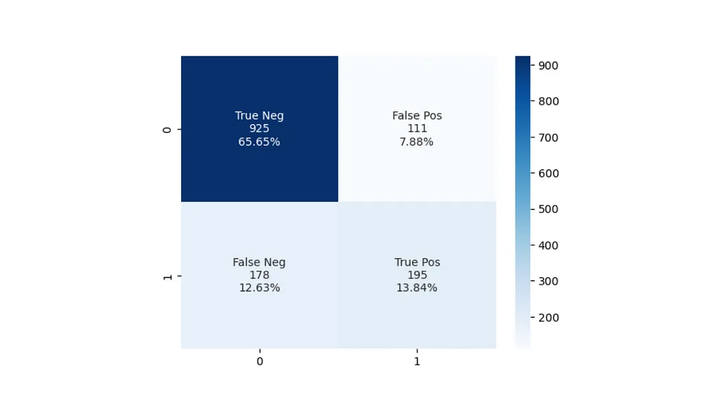
概括：

• 提供真阳性、假阳性、真阴性和假阴性的详细分类。
• 深入了解每个类别的模型性能，有助于识别弱点和偏差。
• 作为计算各种指标的基础，例如精确度、召回率、F1 分数和准确度。
• 可能更难以解释和沟通，因为它不提供整体模型性能的单一值（出于比较目的可能需要该值）。

在 Python 中绘制混淆矩阵的一种简单方法是：

from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay

# 计算混淆矩阵
conf_matrix = confusion_matrix(y_test, y_pred)

# 展示混淆矩阵
disp = ConfusionMatrixDisplay(confusion_matrix=conf_matrix, display_labels=model.classes_)
disp.plot()

1.4 精度 精确度，就是我们模型预测出来的正类中所占的份额。精度的公式为：

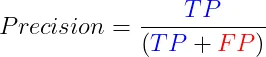
这个指标，特别在那些把假阳性看得比较重的场景下格外重要，比如说过滤垃圾邮件或者是医学上的诊断。但光有精确度还不够，因为它没办法告诉我们假阴性的情况，所以一般会跟召回率一起搭配使用。 概括：

• 在误报的代价特别大的情况下，精确度就显得尤为关键了。
• 易于理解和沟通。
• 但它就是不涉及那些被模型错过的正类，即假阴性的数量。
• 适用于不平衡数据。但是，它应该与其他指标结合使用，因为高精度可能会以牺牲不平衡数据集的召回率为代价

1.5 召回率（灵敏度） 召回率，也叫灵敏度，是评估在所有真正的正例中，有多少被我们的模型正确识别出来的比例。召回率的公式为：

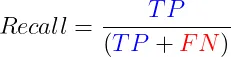
在那些错过真阳性的代价极其重大的场合——比如癌症筛查或者防范信用诈骗，或是在那种正类相对较少的数据集里——召回率的重要性不言而喻。正如召回率需要和精确率一样的搭档一样，为了达到一种评估的平衡，召回率也需要和其他指标一并参考。 概括：

• 在错失真阳性的后果非常严重时，召回率显得格外关键。
• 易于理解和沟通。
• 不考虑误报的数量。
• 适用于不平衡数据。然而，它应该与其他指标结合起来，因为高召回率可能会以牺牲不平衡数据集的精度为代价。

1.6 F1-分数 F1 分数是精确率和召回率的调和平均值，提供了平衡两者的单一指标。 F1 分数的公式如下：

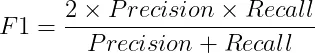
当误报和漏报同样重要并且您寻求精确率和召回率之间的平衡时，F1 分数非常有用。 概括：

• F1-Score 平衡精确度和召回率：当误报和漏报都很重要时很有用。
• 对于不平衡的数据特别有用，在这种情况下，需要在精确度和召回率之间进行权衡。
• 偏向于具有相似精度和召回率的模型，这可能并不总是令人满意的。
• 可能不足以比较不同模型的性能，特别是当模型在误报和漏报之间具有不同的权衡时。

一次性获得准确率、召回率和 F1 分数的最简单方法是使用 scikit-learn 的分类报告：

from sklearn.metrics import classification_report  # 修正导入语句，应该在import和classification_report之间加上空格

# 生成分类报告
# 该报告包括了精确度、召回率、F1分数等关键指标
class_report = classification_report(y_test, y_pred) 

# 打印分类报告
print(class_report)

这为我们提供了两个类别的准确率、召回率和 F1 分数。

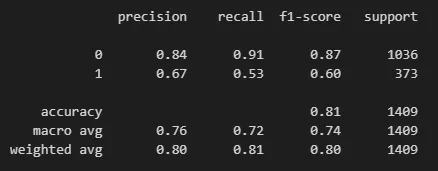
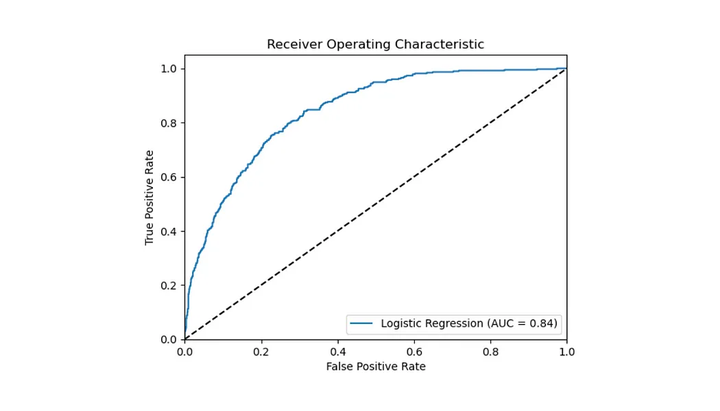
1.7 工作特性曲线下面积（AUC）

AUC衡量的是在不同的判定门槛下，模型识别正类的能力与误将负类判为正类的风险之间的平衡。AUC值满分为1，代表模型预测能力无懈可击，而得分为0.5则意味着模型的预测不过是碰运气。在评估和比较多个模型的表现时，AUC尤其有价值，但为了深入掌握每个模型在各个方面的优劣，最好还是将它与其他性能指标一并参考。

概括：

• 评估各种分类阈值的模型性能。
• 适用于不平衡的数据集。
• 可用于比较不同模型的性能。
• 假设误报和漏报具有相同的成本。
• 非技术利益相关者难以解释，因为它需要了解 ROC 曲线。
• 可能不适合具有少量观测值的数据集或具有大量类别的模型。

我们可以使用以下代码计算 AUC 分数并绘制 ROC 曲线：

# 从sklearn.metrics模块导入roc_auc_score和roc_curve函数用于计算AUC分数和绘制ROC曲线，同时导入matplotlib.pyplot用于绘图
from sklearn.metrics import roc_auc_score, roc_curve 
import matplotlib.pyplot as plt 

# 使用模型对测试集X_test进行概率预测，取正类预测概率为真阳性率的依据
y_pred_proba = my_model.predict_proba(X_test)[:, 1] 

# 利用真实标签y_test和预测概率y_pred_proba计算AUC分数，评估模型的整体性能
auc_score = roc_auc_score(y_test, y_pred_proba) 

# 基于真实标签和预测概率，计算ROC曲线的假阳性率（fpr）和真阳性率（tpr），及不同阈值
fpr, tpr, Thresholds = roc_curve(y_test, y_pred_proba) 

# 使用matplotlib绘制ROC曲线，展示模型的性能。曲线下的面积（AUC）越大，模型性能越好
plt.plot(fpr, tpr, label='My Model (AUC = %0.2f)' % auc_score) 

# 绘制对角线，表示随机猜测的性能水平，作为性能的基准线
plt.plot([0, 1], [0, 1], 'k--') 

# 设定图像的x轴和y轴的显示范围
plt.xlim([0.0, 1.0]) 
plt.ylim([0.0, 1.05]) 

# 设置x轴标签为“误报率”和y轴标签为“真阳性率”，即ROC曲线的标准轴标签
plt.xlabel('误报率') 
plt.ylabel('真阳性率') 

# 设置图表标题为“接收器操作特征”，即ROC曲线的常见名称
plt.title('接收器操作特征') 

# 添加图例，位于图的右下角，展示模型及其AUC分数
plt.legend(loc="lower right") 

# 显示绘制的图像
plt.show()

1.7 对数损失（交叉熵损失） 对数损失用来评估模型预测准确性的一种方法，它对每次预测的正确与否进行奖惩。 这种度量方式通过惩罚错误的预测同时奖励正确的预测来工作。如果对数损失的值越低，意味着模型的性能越好，而当这个值达到0时，就代表这个模型能够完美地进行分类。

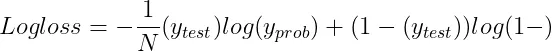
• N是观测值的数量。
• y_test是二元分类问题的真实标签（0 或 1）。
• y_prob是标签为 1 的预测概率。

当你需要对模型的概率预测进行评估时，比如在应用逻辑回归或者神经网络模型的情况下，对数损失就显得尤为重要了。 为了能更深入地掌握模型在各个分类上的表现，最好是将对数损失与其他评估指标一起考虑使用。 概括：

• 概率预测：衡量输出概率估计的模型的性能，鼓励经过良好校准的预测。
• 对数损失可用于比较不同模型的性能或优化单个模型的性能。
• 适用于不平衡数据。
• 对极端概率预测高度敏感，这可能会导致错误分类实例的巨大惩罚值。
• 可能难以向非技术利益相关者解释和沟通。

2 回归指标

2.1 平均绝对误差（MAE）

平均绝对误差（MAE）是用来计算预测值和实际值之间差距绝对值的平均量。简单来说，MAE的计算公式如下：

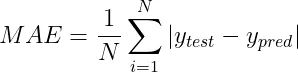
• N是数据点的数量。
• y_pred是预测值。
• y_test是实际值。

概括

• 易于解释：表示平均误差大小。
• 对异常值的敏感度低于均方误差 (MSE)。
• 无错误方向：不表示高估或低估。
• 在某些情况下可能无法捕获极端错误的影响。

在 Python 中，使用 scikit-learn：

from sklearn.metrics import mean_absolute_error  # 修正函数名称，应为小写的 'mean_absolute_error'

# 计算真实值与预测值之间的平均绝对误差 (MAE)
mae = mean_absolute_error(y_true, y_pred)  # 计算MAE

# 打印MAE值，以评估模型预测的准确性
print("MAE:", mae)

2.2 均方误差（MSE） 均方误差（MSE）用于计算预测值与实际值差异的平方后的平均数。MSE 的公式为：

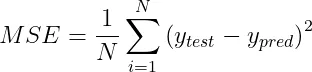
MSE特别对离群值敏感，这是因为它对于较大的误差施加了更重的惩罚，远超过小误差。这一特性根据具体的应用场景，既可能是一个优势也可能是一个劣势。 概括：

• 对极端错误更加敏感。
• 平方误差值可能不如绝对误差直观。
• 与平均绝对误差 (MAE) 相比，受异常值的影响更大。

2.3 均方根误差（RMSE） 均方根误差 (RMSE) 是均方误差的平方根。RMSE 的公式为：

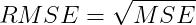
RMSE同样对离群值敏感，和MSE一样，对较大的误差给予较重的惩罚。不过，RMSE的一个显著优势在于它的单位和目标变量保持一致，这使得RMSE更加易于理解和解释。 概括：

• 对极端错误更加敏感。
• 与目标变量相同的单位：
• 与平均绝对误差 (MAE) 相比，受异常值的影响更大。

在 Python 中，使用 scikit-learn：

from sklearn.metrics import mean_squared_error  # 注意修正导入函数名的大小写

# 利用模型对数据集X进行预测，得到预测值y_pred
y_pred = model.predict(X) 

# 计算实际值y和预测值y_pred之间的均方误差（MSE）
mse = mean_squared_error(y, y_pred)  # 注意修正函数名的大小写

# 通过对MSE取平方根，计算均方根误差（RMSE），这一步使得误差单位与目标变量单位一致
rmse = np.sqrt(mse) 

# 输出均方根误差（RMSE），以评估模型预测的准确性
print('Root Mean Squared Error:', rmse)

2.4 平均绝对百分比误差（MAPE）

平均绝对百分比误差（MAPE）是一个衡量预测准确性的指标，它通过计算预测值与实际值之间差异的百分比，然后取这些百分比差异的平均值来实现。MAPE的计算方式可以这样表达：

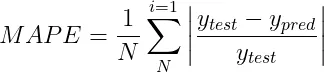
在对比不同模型性能或判断误差的重要程度时，MAPE展现了其独到的价值。 但是，当涉及到接近零的数值时，MAPE的应用就会遇到挑战，因为这时的百分比误差可能会激增，变得异常巨大。

概括：

• 相对误差指标：可用于比较不同尺度的模型性能。
• 易于解释：以百分比表示。
• 零值未定义，这可能发生在某些应用程序中。
• 不对称：高估小实际值的误差，低估大实际值的误差。

Scikit learn 没有 MAPE 函数，但我们可以使用以下方法自己计算：

# 定义一个函数来计算平均绝对百分比误差（MAPE）
def mape(y_true, y_pred): 
    # 计算真实值与预测值之间的绝对差异，然后除以真实值，最后乘以100转换为百分比
    return np.mean(np.abs((y_true - y_pred) / y_true)) * 100

# 使用定义好的MAPE函数，传入真实值y_true和预测值y_pred，计算MAPE
mape_value = mape(y_true, y_pred)  # 修正变量名以避免与函数名相同

# 打印MAPE值，评估模型预测的平均误差百分比
print("MAPE:", mape_value)  # 修正语法错误

2.5 R 平方（决定系数） R平方衡量了模型预测值与实际值之间的一致性，通过计算模型能解释的目标变量方差的比例来评估。具体来说，R平方的计算公式如下：

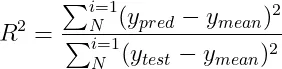
• y_mean是实际值的平均值。
• y_pred是预测值。
• y_test是实际值。

R平方的取值介于0到1之间，其中值越接近1意味着模型的预测能力越强。但是，R平方也存在一定的限制，比如说，即使加入了与目标变量无关的特征，其值也有可能上升。 概括：

• 代表解释方差的比例，使其易于理解和沟通。
• 对目标变量的规模不太敏感，这使得它更适合比较不同模型的性能。
• 偏向于具有许多功能的模型，这可能并不总是令人满意的。
• 不适合评估预测变量和目标变量之间不存在线性关系的模型。
• 可能会受到数据中异常值的影响。

在 Python 中，使用 scikit-learn：

from sklearn.metrics import r2_score 


# 使用r2_score函数计算真实值y_true和预测值y_pred之间的R平方值
r_squared = r2_score(y_true, y_pred) 

# 输出R平方值，以评估模型解释目标变量方差的能力
print("R-squared:", r_squared)

2.6 调整后的 R 平方（Adjusted R-Squared）

Adjusted R-Squared 是对R平方（ R-Squared）的改良，它在计算过程中考虑到了模型中包含的特征数量，从而对模型复杂度进行了调整。调整R平方的计算公式是这样的：

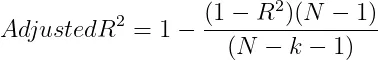
• N是数据点的数量。
• k是特征的数量。

调整后的 R-Squared 可以通过惩罚具有过多特征的模型来帮助防止过度拟合。 概括：

• 修改 R 平方，调整模型中预测变量的数量，使其成为比较具有不同预测变量数量的模型性能的更合适的指标。
• 对目标变量的规模不太敏感，这使得它更适合比较不同模型的性能。
• 惩罚额外变量：与 R 平方相比，降低过度拟合风险。
• 不适合评估预测变量和目标变量之间不存在线性关系的模型。
• 可能会受到数据中异常值的影响。

在 Python 中，我们可以根据 R 平方分数来计算它：

from sklearn.metrics import r2_score 

# 计算模型的R平方值，即模型的解释能力
r_squared = r2_score(y, y_pred) 

# 为了更准确地评估模型性能，计算调整后的R平方值
heroes_count = len(y)  # 观测值数量，类比为武林中的英雄人数
techniques_count = X.shape[1]   # 特征数量，类比为模型中的武学技巧数

# 调整后的R平方值的计算考虑了模型中的特征数量
adj_r_squared = 1 - (((1 - r_squared) * (heroes_count - 1)) / (heroes_count - techniques_count - 1))

# 输出调整后的R平方值
print("调整后的R平方：", adj_r_squared)

3 选择合适的指标

选择合适的评估指标对于确保项目成功至关重要。这一选择应基于具体问题背景、采用的模型类型，以及希望达成的项目目标。以下内容将引导您如何根据这些因素做出明智的决策。

3.1 了解问题背景

在选择指标之前，了解项目背景至关重要。考虑以下因素：

• 机器学习任务类型：选择指标时需要考虑您是在处理分类、回归还是多标签问题，因为不同的问题类型适合不同的评估方法。
• 数据分布情况：面对不平衡数据时，某些指标（如F1分数、精确度、召回率或AUC）可能更加有效，因为它们对类不平衡的敏感度较低。
• 错误的成本：考虑到误报和漏报在您的应用中可能带来的后果不同，选择能够恰当反映这些错误影响的指标十分重要。

3.2 考虑模型目标

模型旨在解决的具体问题同样影响着指标的选择：

• 准确概率估计：如果您的模型需要提供精确的概率预测，对数损失是一个很好的选择。
• 真阳性率与误报的平衡：若要在提高真阳性率的同时降低误报，考虑AUC作为评估标准可能更为合适。

3.3 评估多个指标

为了获得模型性能的全面视图，建议同时考虑多个指标。这样不仅可以揭示模型的长处和短板，还能为模型的优化提供方向。例如：

• 分类任务：同时考虑精确度、召回率和F1分数，可以帮助您在误报和漏报之间找到一个平衡点。
• 回归任务：结合使用如MAE这样的绝对误差指标和MAPE这样的相对误差指标，可以从不同角度评估模型的表现。

[ 抱个拳，总个结 ]

我们探讨了如何选择适合评估机器学习模型性能的指标，强调了指标选择的重要性，并提供了一系列指导原则来帮助你做出明智的选择。以下是各个关键部分的简要回顾：

• 了解问题背景：考虑机器学习任务的类型、数据的分布以及各种类型错误的重要性。
• 考虑模型目标：根据模型旨在解决的具体问题，选择最合适的指标，如准确概率估计或平衡真阳性率与误报。
• 评估多个指标：为了全面了解模型的性能，建议同时评估多个指标，包括精确度、召回率、F1分数（分类任务），以及MAE、MSE、MAPE（回归任务）。

具体到每个指标，我们讨论了：

• 分类指标：介绍了分类任务中的基本概念，如真正例、假正例、真反例、假反例，以及衡量这些分类结果的准确度、混淆矩阵、精确度、召回率、F1分数和AUC。
• 回归指标：探讨了回归任务中的关键指标，包括平均绝对误差（MAE）、均方误差（MSE）、均方根误差（RMSE）、平均绝对百分比误差（MAPE）和R平方（决定系数）。

通过选择正确的验证指标，可以清晰地评估和优化模型性能，确保机器学习项目的成功。希望本指南能够为你的机器学习之旅提供实用的见解和支持。