算法金 | 再见！！！K-means

大侠幸会，在下全网同名「算法金」

0 基础转 AI 上岸，多个算法赛 Top

「日更万日，让更多人享受智能乐趣」

今天我们来聊聊达叔 6 大核心算法之 —— k-means 算法。最早由斯坦福大学的 J. B. MacQueen 于 1967 年提出，后来经过许多研究者的改进和发展，成为了一种经典的聚类方法。吴恩达：机器学习的六个核心算法！

分几部分，拿下：

• k-means 算法的基本原理和工作步骤
• 相关的数学公式和代码示范
• k-means 算法的优缺点
• 误区和注意事项
• k-means 算法的变种和改进
• k-means 算法的实际应用
• k-means 算法与其他聚类算法的对比

1. k-means 算法简介

什么是 k-means 算法

k-means 算法是一种用于聚类分析的非监督学习算法。它通过将数据点划分为 k 个簇，使得每个簇中的数据点尽可能相似，而不同簇之间的数据点尽可能不同。这个算法的名称来源于其中的 k 个簇（clusters）和每个簇的均值（mean）。

k-means 算法的工作原理

k-means 算法的工作原理可以概括为以下几个步骤：

1. 初始化中心点
2. 分配样本到最近的中心点
3. 更新中心点
4. 迭代直到收敛

下面我们来浅浅的感受一下，走你~

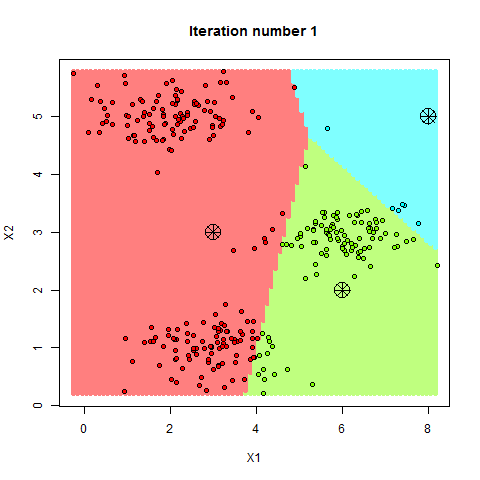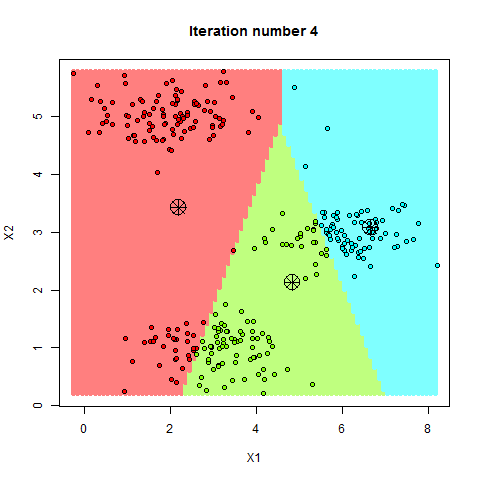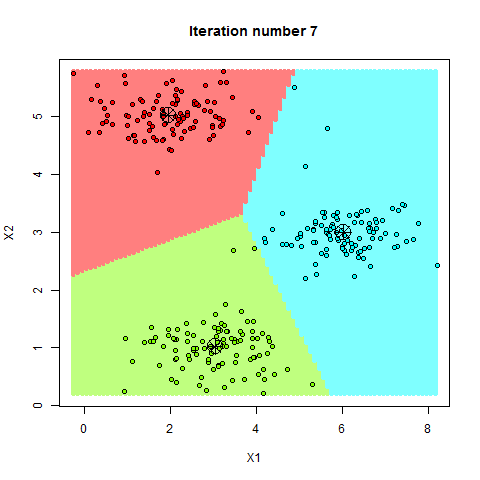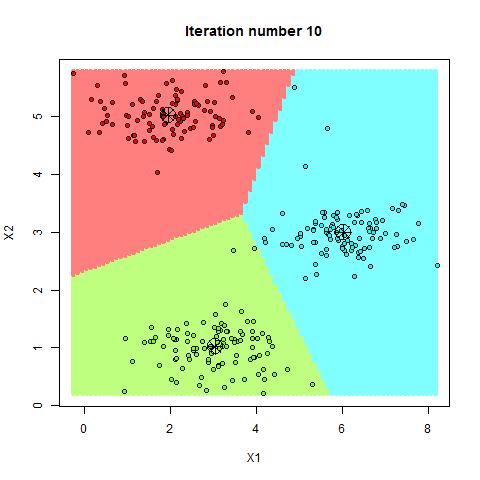
2. k-means 算法的核心步骤

2.1 初始化中心点

在 k-means 算法中，第一步是随机选择 k 个点作为初始中心点。这个步骤非常重要，因为初始中心点的选择会影响最终聚类结果的好坏。如果初始中心点选择不当，可能会导致算法陷入局部最优解。

2.2 分配样本到最近的中心点

一旦初始中心点确定后，我们就可以开始分配样本了。对于每个数据点，我们计算它到所有中心点的距离，并将其分配到距离最近的中心点所属的簇中。通常情况下，我们使用欧氏距离来计算数据点之间的距离。

2.3 更新中心点

在所有数据点被分配到最近的中心点后，我们需要重新计算每个簇的中心点。新的中心点是簇中所有数据点的平均值。

2.4 迭代直到收敛

我们不断重复分配样本和更新中心点这两个步骤，直到中心点不再发生变化或达到预设的迭代次数为止。这时，算法就收敛了，簇的划分结果也就确定了。

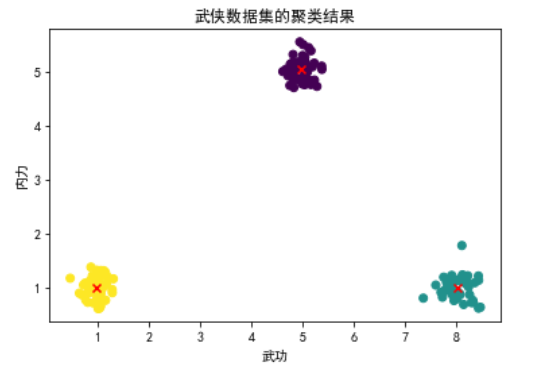
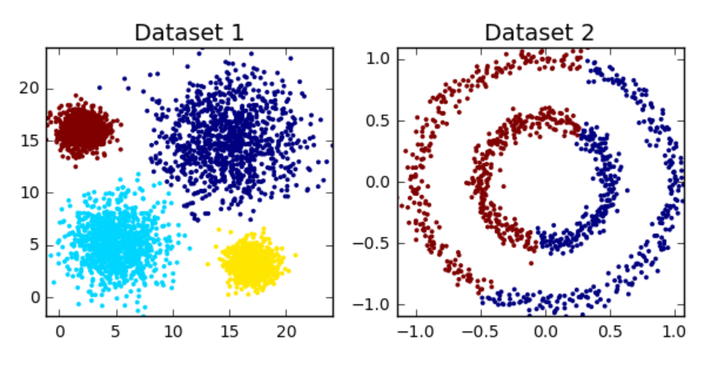
下面，我们用一个结合武侠元素的数据集来演示 k-means 算法的核心步骤：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

# 生成武侠风格的数据集
np.random.seed(42)
data_A = np.random.normal(loc=[1, 1], scale=0.2, size=(50, 2))
data_B = np.random.normal(loc=[5, 5], scale=0.2, size=(50, 2))
data_C = np.random.normal(loc=[8, 1], scale=0.2, size=(50, 2))

data = np.vstack((data_A, data_B, data_C))

# 使用 k-means 算法进行聚类
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(data)
labels = kmeans.labels_
centroids = kmeans.cluster_centers_

# 数据可视化
plt.scatter(data[:, 0], data[:, 1], c=labels, cmap='viridis', marker='o')
plt.scatter(centroids[:, 0], centroids[:, 1], c='red', marker='x')
plt.xlabel('武功')
plt.ylabel('内力')
plt.title('武侠数据集的聚类结果')
plt.show()

每天一个简单通透的小案例，如果你对类似于这样的文章感兴趣。

欢迎关注、点赞、转发~

3. 数学公式和代码示范

3.1 距离度量公式

在 k-means 算法中，最常用的距离度量是欧氏距离。欧氏距离可以衡量两个数据点之间的相似程度，计算公式如下：

其他距离度量方式有，曼哈顿距离 (Manhattan Distance)，切比雪夫距离 (Chebyshev Distance)，闵可夫斯基距离 (Minkowski Distance)等

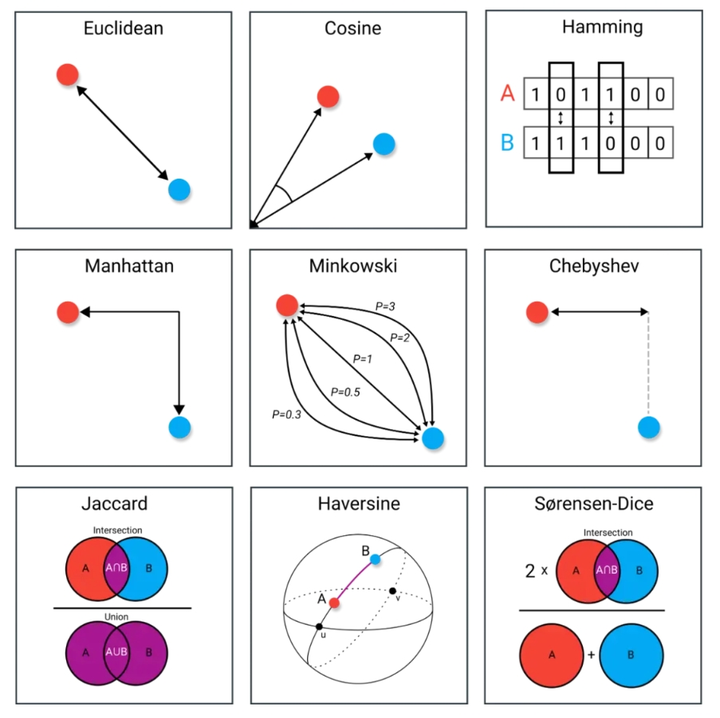
更多细节，见往期微*公号文章：再见！！！KNN

3.2 损失函数（目标函数）

k-means 算法的目标是最小化簇内数据点与中心点之间的总距离，即最小化下式：

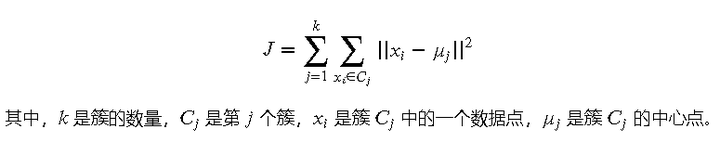
感受一下

3.3 手撕 K means

下面我们用 Python 手动实现 k-means 算法，并通过可视化展示算法的效果。

import numpy as np
import matplotlib.pyplot as plt

# 生成武侠风格的数据集
np.random.seed(7) # （彩蛋）42 是宇宙的答案
data_A = np.random.normal(loc=[1, 1], scale=0.2, size=(50, 2))
data_B = np.random.normal(loc=[5, 5], scale=0.2, size=(50, 2))
data_C = np.random.normal(loc=[8, 1], scale=0.2, size=(50, 2))

data = np.vstack((data_A, data_B, data_C))

def initialize_centroids(data, k):
    """随机选择 k 个点作为初始中心点"""
    indices = np.random.choice(data.shape[0], k, replace=False)
    return data[indices]

def assign_clusters(data, centroids):
    """将每个数据点分配到最近的中心点"""
    distances = np.linalg.norm(data[:, np.newaxis] - centroids, axis=2)
    return np.argmin(distances, axis=1)

def update_centroids(data, labels, k):
    """重新计算每个簇的中心点"""
    new_centroids = np.array([data[labels == i].mean(axis=0) for i in range(k)])
    return new_centroids

def kmeans(data, k, max_iters=100):
    """k-means 算法"""
    centroids = initialize_centroids(data, k)
    for _ in range(max_iters):
        labels = assign_clusters(data, centroids)
        new_centroids = update_centroids(data, labels, k)
        if np.all(centroids == new_centroids):
            break
        centroids = new_centroids
    return labels, centroids

# 运行 k-means 算法
k = 3
labels, centroids = kmeans(data, k)

# 数据可视化
plt.scatter(data[:, 0], data[:, 1], c=labels, cmap='viridis', marker='o')
plt.scatter(centroids[:, 0], centroids[:, 1], c='red', marker='x')
plt.xlabel('武功')
plt.ylabel('内力')
plt.title('武侠数据集的聚类结果')
plt.show()

4. k-means 的优缺点

4.1 k-means 的优势

1. 简单易懂：k-means 算法的概念和实现都非常简单，易于理解和应用。
2. 计算效率高：由于算法的时间复杂度较低，k-means 适合处理大规模数据集。
3. 结果直观：通过可视化，k-means 聚类结果清晰明了，容易解释。

4.2 k-means 的劣势

1. 需要预设簇数 k：k-means 需要用户事先指定簇的数量 k，而在实际应用中，合适的 k 值往往很难确定。
2. 对初始中心点敏感：k-means 对初始中心点的选择非常敏感，不同的初始中心点可能导致不同的聚类结果，甚至局部最优解。
3. 只适用于凸形簇：k-means 假设簇是球形的，这使得它难以处理非凸形的簇结构。
4. 受异常值影响大：异常值可能会显著影响中心点的计算，从而影响聚类结果。

5. 误区和注意事项

5.1 误区：选择 k 值的误区

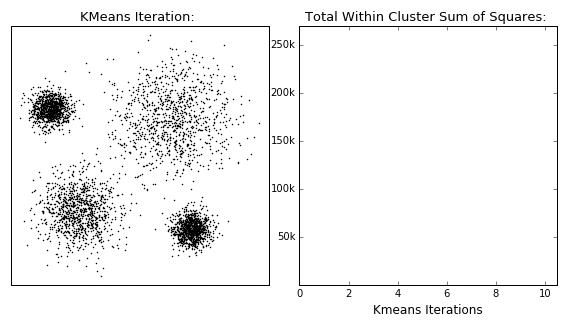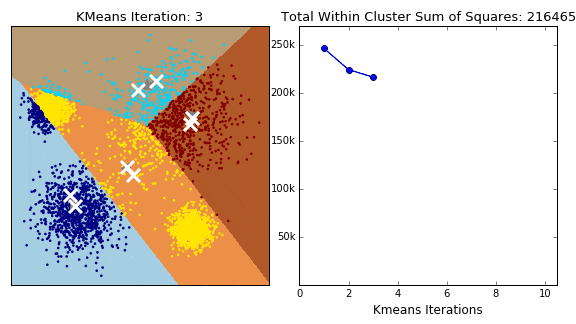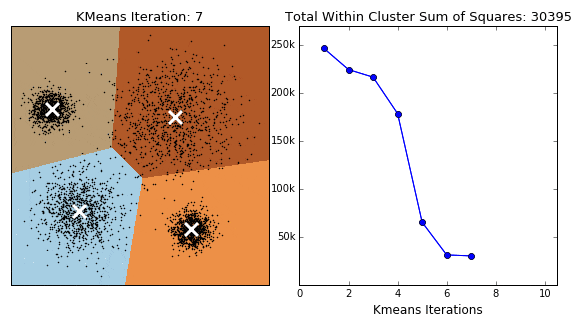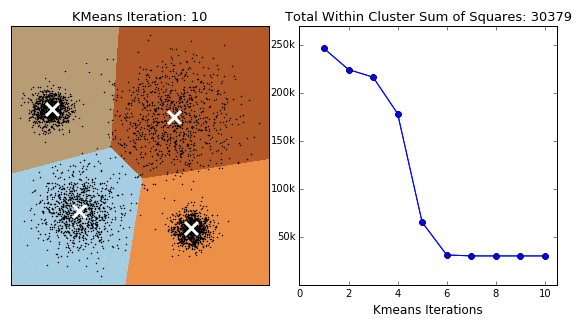
一个常见的误区是随意选择 k 值。选择合适的 k 值对于 k-means 算法的效果至关重要。如果 k 过小，可能会导致欠拟合，无法捕捉数据中的全部信息；如果 k 过大，可能会导致过拟合，使得模型对数据的细节过于敏感。常用的方法有肘部法（Elbow Method）和轮廓系数法（Silhouette Score）来选择合适的 k 值。

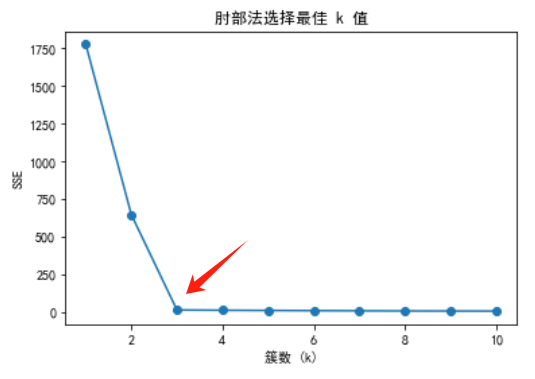
肘部法（Elbow Method）

肘部法是一种常用的选择 k 值的方法。其基本思想是通过计算不同 k 值下的总误差平方和（SSE），绘制 SSE 随 k 值变化的曲线，当曲线出现“肘部”时，对应的 k 值即为最佳选择。SSE 随 k 值增加而递减，当 k 值达到某个临界点后，SSE 的减小速度明显减缓，这个临界点对应的 k 值就是肘部。

肘部法的步骤如下：

1. 运行 k-means 算法，令 k 从 1 取到最大值。
2. 计算每个 k 值对应的 SSE（误差平方和）。
3. 绘制 k 值与 SSE 的关系图，找出肘部点。

from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

def elbow_method(data, max_k):
    sse = []
    for k in range(1, max_k + 1):
        kmeans = KMeans(n_clusters=k, random_state=42)
        kmeans.fit(data)
        sse.append(kmeans.inertia_)

    plt.plot(range(1, max_k + 1), sse, marker='o')
    plt.xlabel('簇数 (k)')
    plt.ylabel('SSE')
    plt.title('肘部法选择最佳 k 值')
    plt.show()

# 使用肘部法选择最佳 k 值
elbow_method(data, 10)

轮廓系数法（Silhouette Score）

轮廓系数法通过计算数据点的轮廓系数来评估聚类结果的质量。轮廓系数介于 -1 和 1 之间，数值越大表示聚类效果越好。轮廓系数不仅考虑了同一簇内数据点的紧密程度，还考虑了不同簇之间的分离程度。

轮廓系数法的步骤如下：

1. 运行 k-means 算法，令 k 从 2 取到最大值。
2. 计算每个 k 值对应的平均轮廓系数。
3. 绘制 k 值与平均轮廓系数的关系图，选择平均轮廓系数最高的 k 值。

from sklearn.metrics import silhouette_score

def silhouette_method(data, max_k):
    silhouette_scores = []
    for k in range(2, max_k + 1):
        kmeans = KMeans(n_clusters=k, random_state=42)
        labels = kmeans.fit_predict(data)
        score = silhouette_score(data, labels)
        silhouette_scores.append(score)

    plt.plot(range(2, max_k + 1), silhouette_scores, marker='o')
    plt.xlabel('簇数 (k)')
    plt.ylabel('平均轮廓系数')
    plt.title('轮廓系数法选择最佳 k 值')
    plt.show()

# 使用轮廓系数法选择最佳 k 值
silhouette_method(data, 10)

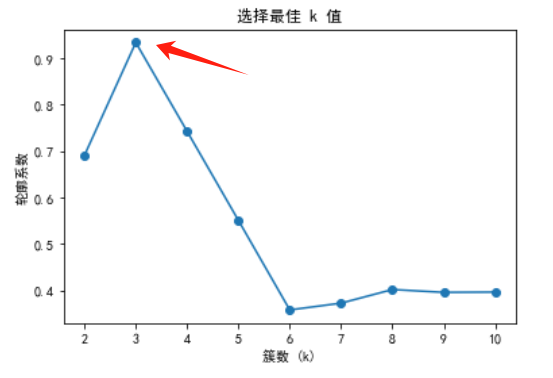
通过这两种方法，我们可以更加科学和合理地选择 k 值，从而提高 k-means 算法的聚类效果。

5.2 注意事项：数据标准化

在使用 k-means 算法之前，对数据进行标准化处理非常重要。由于不同特征的量纲不同，直接使用未标准化的数据会导致距离计算时某些特征的影响被放大。通常情况下，我们使用 z-score 标准化方法：

from sklearn.preprocessing import StandardScaler

# 数据标准化
scaler = StandardScaler()
data_standardized = scaler.fit_transform(data)

# 使用标准化后的数据进行聚类
kmeans = KMeans(n_clusters=3, random_state=42)
labels = kmeans.fit_predict(data_standardized)
centroids = kmeans.cluster_centers_

# 数据可视化
plt.scatter(data_standardized[:, 0], data_standardized[:, 1], c=labels, cmap='viridis', marker='o')
plt.scatter(centroids[:, 0], centroids[:, 1], c='red', marker='x')
plt.xlabel('标准化后的武功')
plt.ylabel('标准化后的内力')
plt.title('标准化数据的聚类结果')
plt.show()

5.3 误区：初始中心点选择的重要性

有些铁子们可能会忽略初始中心点的选择，直接使用默认的随机初始化。其实，初始中心点的选择会显著影响聚类结果。为了避免局部最优解，我们可以使用 k-means++ 算法进行初始化，这样可以有效提高算法的稳定性和收敛速度。

# 使用 k-means++ 初始化进行聚类
kmeans_pp = KMeans(n_clusters=3, init='k-means++', random_state=42)
labels_pp = kmeans_pp.fit_predict(data)
centroids_pp = kmeans_pp.cluster_centers_

# 数据可视化
plt.scatter(data[:, 0], data[:, 1], c=labels_pp, cmap='viridis', marker='o')
plt.scatter(centroids_pp[:, 0], centroids_pp[:, 1], c='red', marker='x')
plt.xlabel('武功')
plt.ylabel('内力')
plt.title('k-means++ 初始化的聚类结果')
plt.show()

5.4 注意事项：避免局部最优解

为了进一步避免陷入局部最优解，可以多次运行 k-means 算法，并选择最优的聚类结果。这样做可以显著提高最终结果的稳定性和准确性。

# 多次运行 k-means 算法并选择最优结果
best_inertia = np.inf
best_labels = None
best_centroids = None

for _ in range(10):
    kmeans = KMeans(n_clusters=3, random_state=42)
    labels = kmeans.fit_predict(data)
    if kmeans.inertia_ < best_inertia:
        best_inertia = kmeans.inertia_
        best_labels = labels
        best_centroids = kmeans.cluster_centers_

# 数据可视化
plt.scatter(data[:, 0], data[:, 1], c=best_labels, cmap='viridis', marker='o')
plt.scatter(best_centroids[:, 0], best_centroids[:, 1], c='red', marker='x')
plt.xlabel('武功')
plt.ylabel('内力')
plt.title('多次运行后的最佳聚类结果')
plt.show()

6. k-means 算法的变种和改进

6.1 k-means++ 算法

k-means++ 是 k-means 算法的一种改进版本，旨在通过一种更巧妙的初始中心点选择方法来提高算法的稳定性和收敛速度。k-means++ 的核心思想是在选择初始中心点时，让新的中心点尽可能远离已选择的中心点，从而减少随机初始化带来的不稳定性。

k-means++ 初始化步骤：

1. 随机选择一个数据点作为第一个中心点。
2. 对于每一个数据点 𝑥𝑥，计算它到最近已选中心点的距离 𝐷(𝑥)𝐷(𝑥)。
3. 根据 𝐷(𝑥)𝐷(𝑥) 的概率分布随机选择下一个中心点，选择概率与 𝐷(𝑥)𝐷(𝑥) 正相关。
4. 重复步骤 2 和 3，直到选择出 k 个中心点。

6.2 Mini-Batch k-means

Mini-Batch k-means 是 k-means 的另一个改进版本，适用于大规模数据集。它通过使用小批量的数据进行迭代，减少了每次迭代的计算量，从而大大加快了聚类速度。Mini-Batch k-means 的核心思想是每次仅随机选取一部分数据进行中心点的更新。

6.3 其他变种

除了 k-means++ 和 Mini-Batch k-means 之外，还有许多 k-means 的变种和改进算法，例如：

1. Bisecting k-means：通过递归地将数据集分成两部分来进行聚类，适用于层次聚类。
2. Fuzzy k-means：允许一个数据点属于多个簇，通过模糊隶属度来表示，适用于模糊聚类。
3. Kernel k-means：通过使用核函数将数据映射到高维空间进行聚类，适用于非线性数据。

这些改进算法在不同的应用场景中具有各自的优势，可以根据具体需求选择合适的算法。

7. k-means 算法的应用和案例

7.1 图像压缩

k-means 算法在图像压缩中的应用非常广泛。通过将图像中的像素点聚类为 k 个颜色簇，可以有效减少图像的颜色数量，从而实现图像压缩。下面是一个使用 k-means 进行图像压缩的示例。

from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np
from skimage import io

# 读取图像
image = io.imread('https://example.com/image.jpg')
image = np.array(image, dtype=np.float64) / 255

# 将图像数据重塑为二维数组
w, h, d = image.shape
image_array = np.reshape(image, (w * h, d))

# 使用 k-means 进行图像压缩
kmeans = KMeans(n_clusters=16, random_state=42).fit(image_array)
labels = kmeans.predict(image_array)
compressed_image = kmeans.cluster_centers_[labels].reshape(w, h, d)

# 显示原始图像和压缩后的图像
fig, ax = plt.subplots(1, 2, figsize=(12, 6), subplot_kw={'xticks': [], 'yticks': []})
ax[0].imshow(image)
ax[0].set_title('原始图像')
ax[1].imshow(compressed_image)
ax[1].set_title('压缩图像')
plt.show()

7.2 客户分群

在市场营销中，k-means 算法可以用来对客户进行分群，从而更好地制定营销策略。通过分析客户的消费行为、偏好等特征，将客户分成不同的群体，有助于企业针对不同客户群体制定个性化的营销方案。

7.3 其他实际应用

除了图像压缩和客户分群，k-means 算法在其他领域也有广泛的应用，例如：

1. 文档分类：将文档聚类为不同的主题，有助于文档的自动归档和检索。
2. 城市规划：根据居民的地理位置和人口密度，将城市划分为不同的区域，优化城市资源配置。
3. 基因表达分析：在生物信息学中，k-means 用于分析基因表达数据，找出具有相似表达模式的基因群体。

通过这些实际应用的案例，可以看出 k-means 算法在不同领域的强大实用性。

8. 横向对比：k-means 与其他聚类算法

8.1 k-means vs. 层次聚类

原理

• k-means：通过迭代优化中心点来最小化簇内平方误差。
• 层次聚类：通过构建树状结构（树状图）来逐步聚合或拆分数据点。

适用场景

• k-means：适用于大规模数据，且簇的形状是球形的情况。
• 层次聚类：适用于小规模数据，且需要层次结构或簇的形状不规则的情况。

优缺点对比

• k-means：计算速度快，但对初始点敏感，适合处理大数据。
• 层次聚类：无需预设簇数，但计算复杂度高，不适合大数据。

8.2 k-means vs. DBSCAN

原理

• k-means：基于均值和距离的聚类算法。
• DBSCAN：基于密度的聚类算法，通过寻找高密度区域形成簇。

适用场景

• k-means：适用于数据均匀分布的情况。
• DBSCAN：适用于簇形状不规则且有噪声的数据。

优缺点对比

• k-means：需要预设簇数，对异常值敏感。
• DBSCAN：无需预设簇数，能识别噪声，但参数选择困难。

8.3 k-means vs. GMM

原理

• k-means：通过最小化簇内平方误差进行聚类。
• GMM (高斯混合模型)：假设数据由多个高斯分布组成，通过期望最大化（EM）算法进行聚类。

适用场景

• k-means：适用于簇形状均匀的数据。
• GMM：适用于簇形状复杂的数据，能够处理概率归属问题。

优缺点对比

• k-means：简单高效，但对簇形状有假设限制。
• GMM：灵活性高，但计算复杂度高，需要选择适当的高斯分布数量。

通过这些对比，我们可以看到不同聚类算法在不同应用场景下的优缺点，选择合适的算法可以更好地解决具体问题。

[ 抱个拳，总个结 ]

• 了解了 k-means 算法的基本概念、工作原理和应用场景。
• 学习了 k-means 算法的核心步骤，包括初始化中心点、分配样本、更新中心点和迭代直到收敛。
• 掌握了 k-means 算法的数学公式，如欧氏距离和损失函数，通过代码示例加深理解。
• 分析了 k-means 的优缺点，强调了选择合适 k 值和数据标准化的重要性。
• 探讨了 k-means 算法的变种和改进，如 k-means++ 和 Mini-Batch k-means。
• 通过图像压缩和客户分群等案例展示了 k-means 的实际应用效果。
• 比较了 k-means 与其他聚类算法（如层次聚类、DBSCAN 和 GMM），帮助理解不同算法的适用场景和优缺点。

希望通过这篇文章，大家能对 k-means 算法有一个全面的认识，并掌握其实际应用的方法。如果你有任何疑问或需要进一步探讨，欢迎随时留言交流。

吴恩达：机器学习的六个核心算法！

回归算法，逻辑回归，决策树算法， 神经网络，K-means（本文），梯度下降（TODO，催更请留言）

- 科研为国分忧，创新与民造福 -

日更时间紧任务急，难免有疏漏之处，还请大侠海涵

内容仅供学习交流之用，部分素材来自网络，侵联删

[ 算法金，碎碎念 ]

全网同名，日更万日，让更多人享受智能乐趣

如果觉得内容有价值，烦请大侠多多 分享、在看、点赞，助力算法金又猛又持久、很黄很 BL 的日更下去；

同时邀请大侠 关注、星标 算法金，围观日更万日，助你功力大增、笑傲江湖