基于纳什均衡的多智能体强化学习交通信号控制
纳什均衡理论基本概念
- 基本概念
- 纳什均衡：要其他参与者不改变自己的策略的情况下，没有任何一个参与者可以通过改变策略获得更多的收益。任何静态的博弈至少有一个纳什均衡。
- 多交叉路口交通信号控制问题
多交叉路口交通信号控制就是在城市的多个路口，同时控制不同路口的交通信号，形成一个联合控制动作，提升城市整体的通行能力。
- 从博弈论到多智能体强化学习
- 多交叉路口交通信号控制问题定义
在基于纳什均衡和 MARL 的多交叉路口交通信号控制问题中，我们定义：每一个控制交通灯变化（时长）的行为主体是Agenti(i ∈ N )；πi为当前 Agent
（Agenti）所有可接受的交通灯时长控制策略，奖励 Ri是环境表示 Agenti和其他 Agent（Agent−i）在整个交通环境下的拥堵程度 (可以按照车辆排队长
度、通过路口的平均速度具体指标计算），拥堵程度越低，奖励越大。
- 基于纳什均衡的优势行动者评论家算法
- 深度强化学习的相关的算法分为基于价值函数、基于策略、基于结合策略和价值函数三类。
- 基于结合策略和价值函数的方法的优点：
（1）避免了策略梯度算法中奖励函数是通过与环境的实际交互进行估计不稳定的缺点
（2）避免了价值函数中不能有效进行连续动作策略的输出的缺点 - “演员-评论家”（Actor-Critic）模型就是典型的结合结合策略和价值函数的方法。Actor-Critic 用 Q 学习来估计奖励函数，取代在每次与环境中交互中估算，
可以使奖励估算的过程更加稳定。
-Nash-A2C 算法（基于纳什均衡的优势行动者评论家算法）
优势函数代表着 Qˆ 和 Vˆ 的差值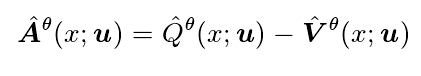
其中，优势函数 Advance 为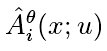 
， 
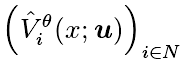为用于评估奖励的价值函数。Q 函数
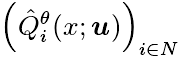用于奖励预测。
分离参数集合 θ 为价值函数参数集合和策略函数参数集合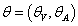
其中 θV代表值函数的模型 ˆV θV的参数; θA代表智能体（参与者）动作选择策略的模型参数 ˆπθA。算法目标为：将采样的样例的损失和 Nash-Bellman 方程联系起来，最小化：
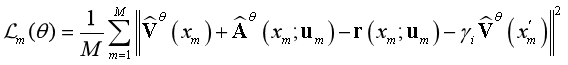
为了简化上式表达，我们定义：
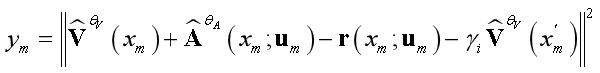
引入记忆缓冲区（replaybuffer）来存储三元组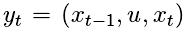 
，分别代表环境的先前状态 xt−1，在该状
态下执行的操作 u，环境的下一个状态 xt，和经过这个状态的奖励 yt。我们从replay buffer 中随机采样一段记忆信息，使用随机梯度下降（SGD）更新参数。该算法还使用 ϵ-贪婪探索，优化动作策略。
Nash-A2C 算法结构：
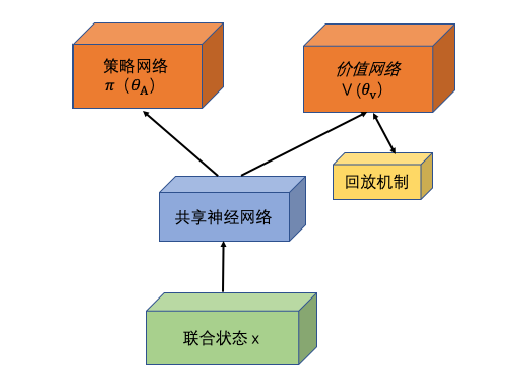
算法步骤：
- Nash-A3C 算法
Nash-A3C 算法在多个环境副本上并行地异步执行多个 Nash-A2C 算法（网络结构如图4-3所示），不同的环境采用不同的策略，经历不同的状态，有不同的智能体与环境交互的历史记录。
Nash-A3C 算法结构：
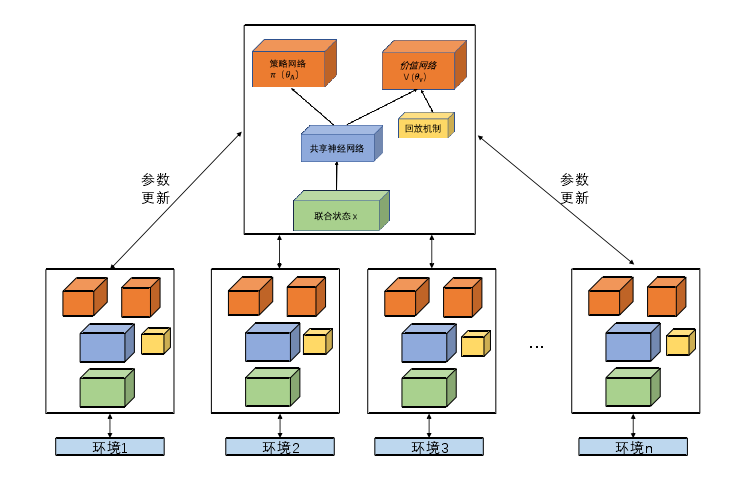
算法步骤：
- 仿真实验
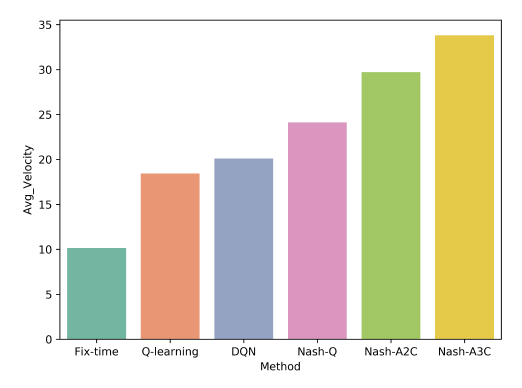
分别采用固定时长 、Q 学习 、DQN、Nash-Q、Nash-A2C、Nash-A3C 交通信号控制的算法在基于真实交通流量的城市多交叉路口仿真平台 USE 仿真环境中进实验并收集实验结果。
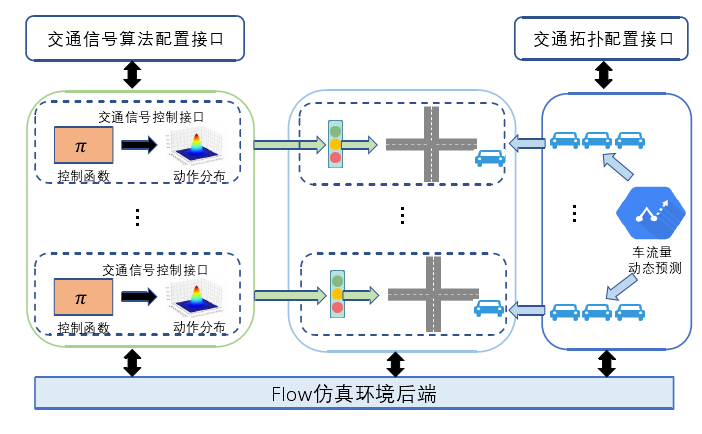
- 仿真环境设置
配置交叉路口 27 个，连接道路 45 条。每一个交叉路口的初始的进入车流量，离开车流量按照 MTD 的数据进行配置，将交通灯控制接口算法配置到每一个路口上，通过算法接口进行
交通信号时长控制，并根据当前和历史流量动态调整交通流量
- 实验过程
在仿真环境中输入真实的车流量数据。然后通过算法接口分别配置固定时长 、Q 学习 、DQN、Nash-Q、Nash-A2C、Nash-A3C 交通信号控制的算法。每隔 15 分钟通过交通流量预测
系统更新一次每个交通路口的车流量，记录每分钟每个交通路口的车辆等待时长和车辆平均速度（视为环境反馈奖励），进行 1000 Episode（回合）训练。
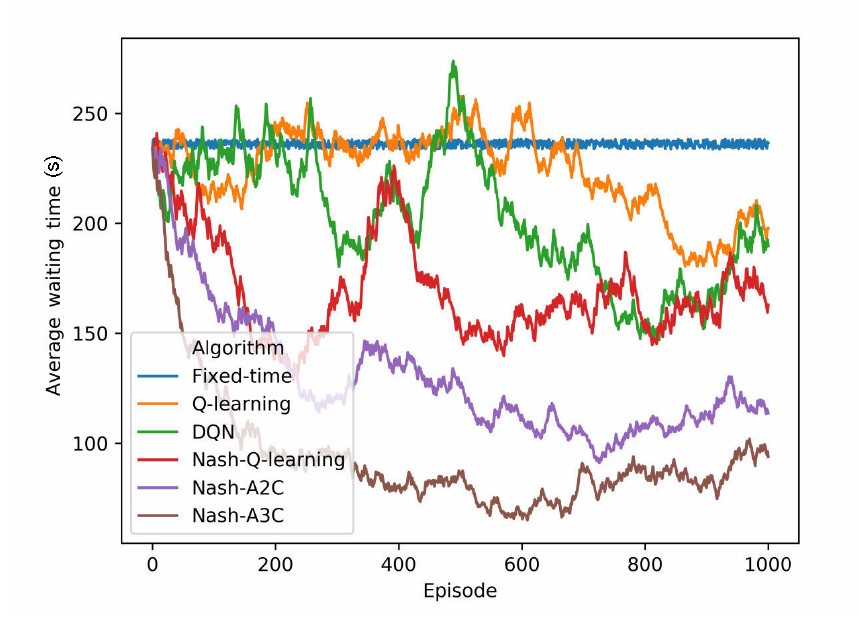
分析：第四节提出的Nash-A2C和Nash-A3C算法的训练收敛效果优于其他基线方法。 - 实验结果：
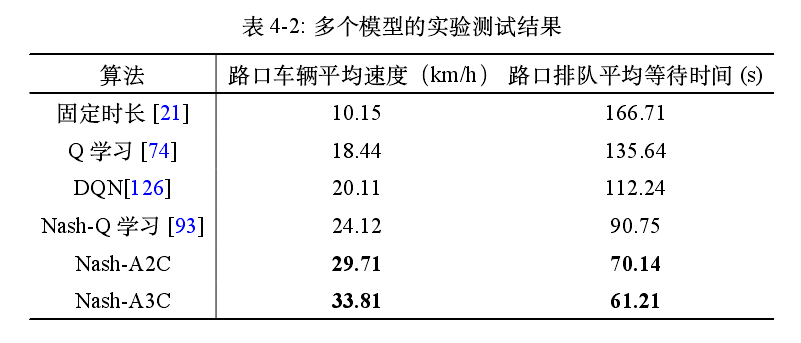
测试过程中每个 Episode 中每个路口平均等待时间的结果：
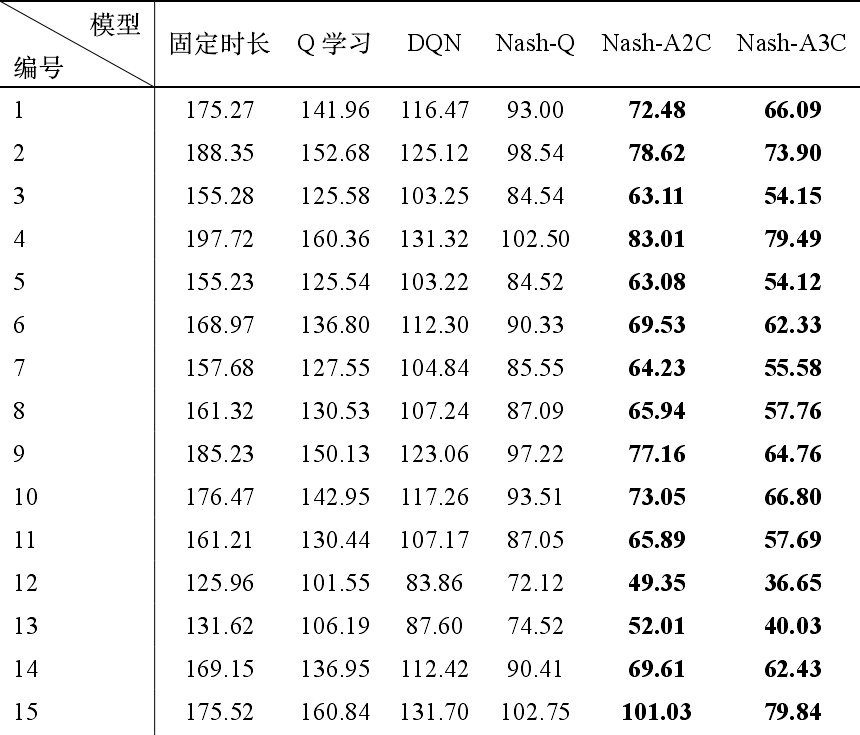
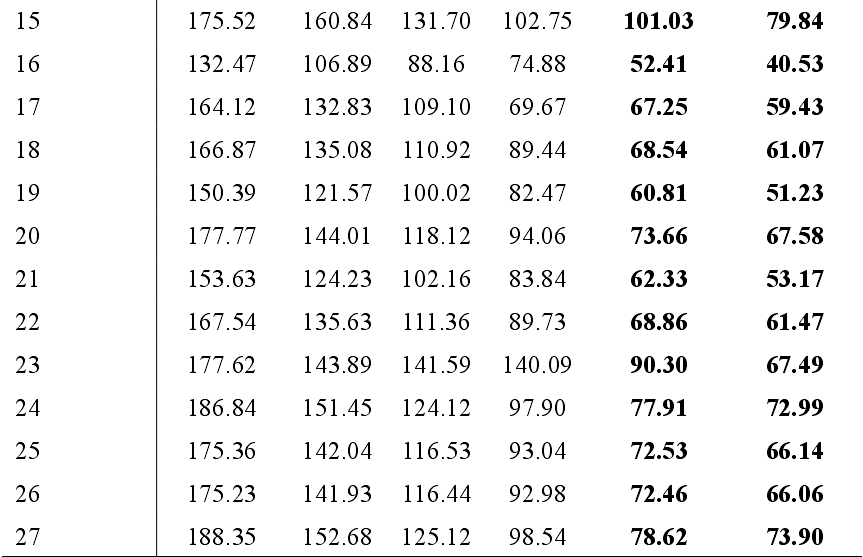
每个交叉路口的平均等待时间热点图：
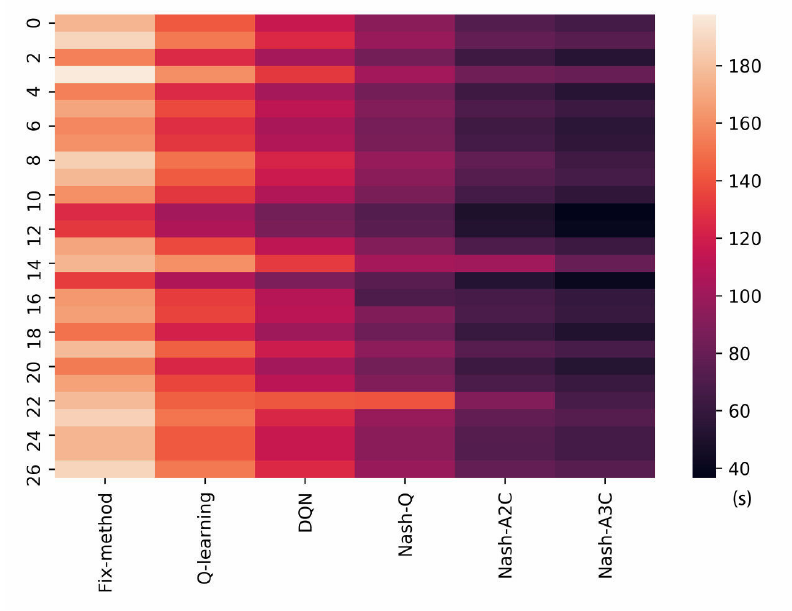
每个模型的平均通过速度（km/h）：
每个模型的平均等待时长（s）
- 实验小结
MARL 算法中引入纳什均衡理论，对于提升 MARL 的交通信号的控制效果具有正向作用。这也为后续章节算法使用纳什均衡理论建立一定的基础。
