第一章绪论笔记1
一、复杂网络的结构特性
1. 度分布
- 一个节点的重要程度可以用和这个节点度相同的节点的数量Nk占所有节点数量TN的比例。形式化的表示为：P（k）=Nk/TN
- 网络的平均度：用网络度的一阶矩来表示，表示所有结点的度的平均值。形式化表示为：
=ΣkP（k），就是度和这个度的节点占全部节点的比例的乘积，然后求和。度分布的异质性可以用网络度分布的二阶矩来表示，
形式化描述为：<k²>=Σk²P（K）。就是度的平方和这个度的节点占全部节点的比例的乘积，然后求和。
2. 簇系数 - 簇系数表征了系统内成团特性，反映的是网络的聚合程度。簇系数的定义为：Ci=2Ri/｛Ki（ki-1）｝。其中，Ci为i结点的簇系数，Ki（ki-1）/2为连接度为ki的i节点的邻居结点之间相互连接的边的最大数量，
如果边数为Ki（ki-1）/2，说明节点i和他的Ki个邻居节点为全连接网络。Ri为实际连接这些节点的边的数量。整个网络的簇系数C=ΣCi/TN。当C=1，网络为全连接网络，C=0，所有结点都为孤立结点或星型结构。
3. 平均距离 - 最短距离dij：指的是从节点i到节点j所经过的最短路径上的边数。
- 网络的直径D：网络中连接两个节点的最长路径，D=maxdij
- 网络的平均距离：
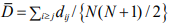，其中，N为无向网络的节点数。D为网络中任意两个节点之间的最短距离求平均值来获得的。
研究表明，实际的网络通常都具
有较短的平均距离。
4. 介数 - 介数Bi：网络中所有最短路径经过节点i的概论。用公式表示为：
，其中
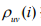指的是从节点u到v中经过i节点的最短路径的数量，
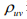指的是所有从节点u到v的最短路径的数量。
二、网络结构的数学生成方法
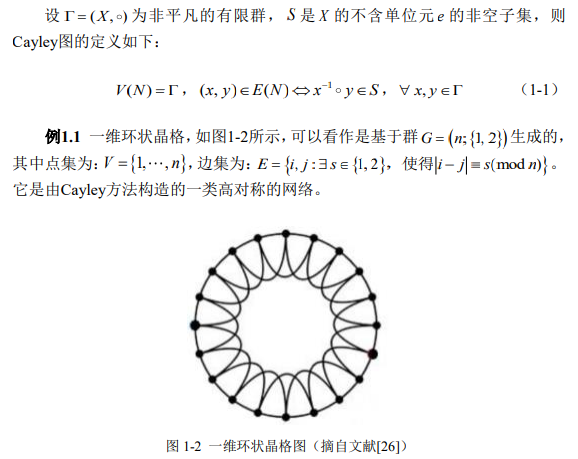
- Cayley 方法 （！ 没看懂，后续继续学习）
- Cayley 方法的特点：由Cayley方法得到的网络具有高对称性，因为它是基于群的概念得到。
- 群的基本概念： 非空集X和作用在它上面的二元运算○组成的代数结构
称为群。
○是某一种二元运算，可以是普通的加法、惩罚，也可以是modn加法等。
- 封闭性：即对于任意的x,y∈X，均满足x○y∈X。
- 结合律：对于任意的x，y，z ∈X，有
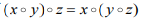
- 单位元：存在e∈X，满足对于任意的x∈X，
- 逆元：对于任意的x∈X，存在相应的y∈X，满足
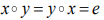，此时y称为x的逆元，记为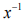
例如：
- 群的构造方法：
- 笛卡尔乘积方法
笛卡尔乘积方法是另一种有效的网络生成方法，它可以从指定的若干小网络（如环状网络）构造出较大网络。通过使用笛卡尔乘积方法构造出来的网络，由于将原有的小网络作为它的子网络，
必然会继承原先小网络所具有的连通性和正则性等网络特性。（小网络通过笛卡尔乘积方法构造出大网络，大网络会继承小网络的连通性和正则性）。
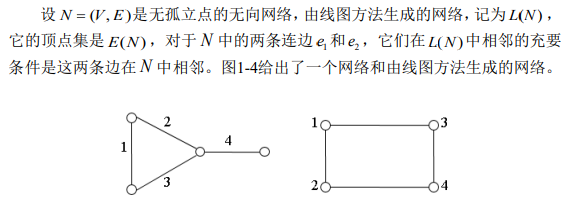
- 线图方法
由已知网络构造更大网络的一种重要方法。线图中的许多参数，例如点的度、连通性等都可以方便地从原图中导出。
三、常见的复杂网络模型
- 规则网络
规则网络被定义为一类具有度分布均匀，平均路径长度较长，平均路径长度和网络大小成比例等显著特点的复杂网络。 - 随机网络
- 定义：在随机网络中，节点之间是否进行连接是未知的，而且存在一定的概率关系。给定网络节点总数，网络中任意两个节点之间以一定的概率进行连边，连边概率的变化会直接影响到随机网
络的拓扑结构性质。 - 特点：簇系数小，平均路径长度短和接近于泊松分布的度等特征。泊松分布的概率函数为：
，
泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。 泊松分布适合于描述单位时间内随机事件发生的次数。 - 构造方式：有N个孤立的点，这N个点最多有
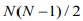条可能的连接，以一定的概论p在任意两个未连接
的节点之间建立一条连边，最终可以得到具有p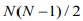条连边的随机网络。
- 小世界网络
大量的现实网络具有较短的网络平均路径，较高的聚类系数，以及指数分布的连接度等结构特征。Watts等[30]在1998年首次提出具有小世界效应的WS小世界网络模型。通过顺时针对最近邻耦合网络中的节点
进行“断边重连”操作，构造出WS小世界网络模型。该网络模型的平均路径较短且簇系数较大，更加符合现实世界中复杂网络的结构特征。
- WS小世界网络模型构造过程：
个人理解：在环形规则网络中遍历每一个节点，对于连接节点的每条边以概论p来决定是否进行断边重连，如果要断边重连，先断边，然后在整个网络中随机挑选一个节点连接，这个节点不能是本身，也不能出现重复连接。 - WS小世界网络模型生成示意图：
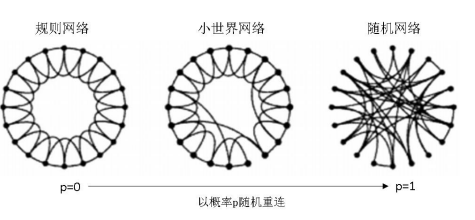
在WS小世界网络模型的建立过程中，由于使用随机重连的机制会在一定程度上损坏原有网络的连通性，从而导致网络中出现一些孤立节点。为了有效解决该问题，Newman等[31]在1999年进一步提出NW小世界网络模型，
原先在WS小世界网络中使用的随机重连机制被随机加边机制所替代，可以有效避免随机重连破坏原来网络的连通性。NW小世界网络模型的其它构造方法和WS小世界网络模型基本相同，下面详细介绍NW小世界网络模型的构造过程。 - NW小世界网络模型构造过程：首先，定义一个环形的规则网络，该网络具有N个节点，每个节点都只和它最近邻的k个节点相连；然后以一定的概率p对随机选取的两个未连接的节点进行连接。需要注意的是，在进行随机加
基于记忆与期望的网络演化博弈研究边的过程中，同样需要保证不能出现重复连边和自我连接的情况，即不能重复连接两个节点和不能用一条线连接某个节点自身。通过保证这两个约束条件，能够保证网络的连通性不会
遭到破坏。此外，当N足够大，p足够小时，WS小世界模型就等价于NW小世界模型。
个人理解：WS每个节点和K条边相连，系统以p的概率来断边重连。NW每个节点只和K个邻居节点相连，以概论p对随机选取的两个未连接的节点进行连接。 - NW小世界网络模型生成示意图：
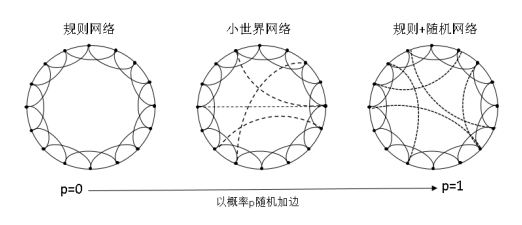
- 无标度网络
- 特点：以真实重现大量真实网络的度分布的特征，从而解释了幂律分布的产生机理。
- 持续增长 ：持续增长是指大部分真实网络的节点不是固定的，而是随着时间的演化，它们的规模会不断动态增大
- 优先连接：新增节点会优先与连接度比较大的节点进行连接。然而优先连接会导致连接度大的点会跟越来越多的节点连接，这也是造成无标度网络中有少量连接度很高的节点存在的原因。
- 构造算法：无标度网络模型的构造算法如下：在初始时刻，只有m0个连通的节点，即任意两个节点都进行连接，在之后的每个时间步中，都会有一个新的节点加入到现有网络中。新加入节点的m条边分别连接到网络中已经存在的m0个不同的节点上，且满足
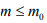。网络中旧节点是否会被连接的概率正比于该节点的度ki，形式化表示为
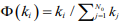，这里N0表示当前系统的节点总数。通过这样的方式构造出来的无标度网络，在经过时间间隔t后，将会得到一个节点总数为
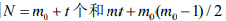条边的网络。 - 不足和缺陷：
- 当网络演化的时间足够长时，会逐渐形成规模较大的网络，与此同时，网络中节点的度分布会呈现幂律分布，即：
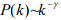，而实际复杂网络的幂指数的取值范围为：
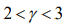。 - 随着网络规模的不断增大，无标度网络的簇系数也会逐渐趋近于零。
