机器学习--最优化
一、说在前面
今天学习的是机器学习当中的最优化的问题,如何将自己的模型更加优化。
二、笔记
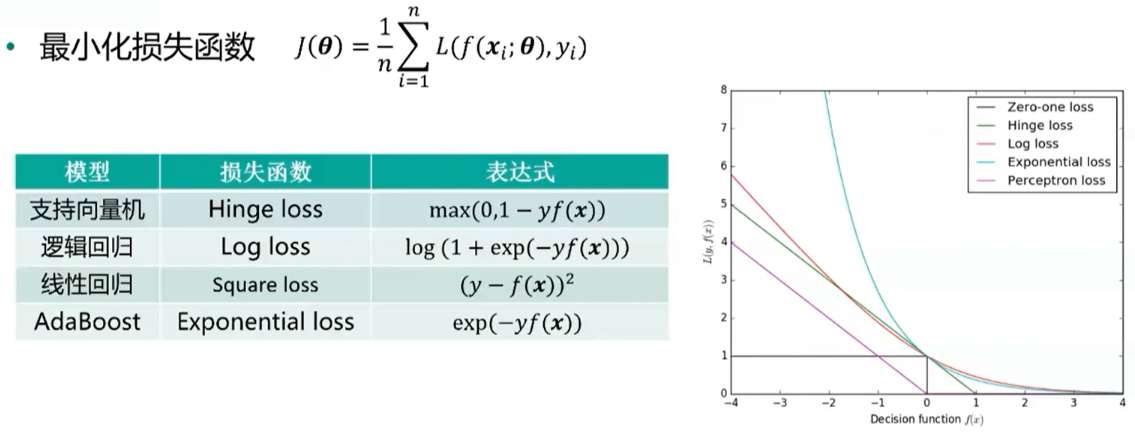
1、机器学习模型的优化目标 最小化损失函数
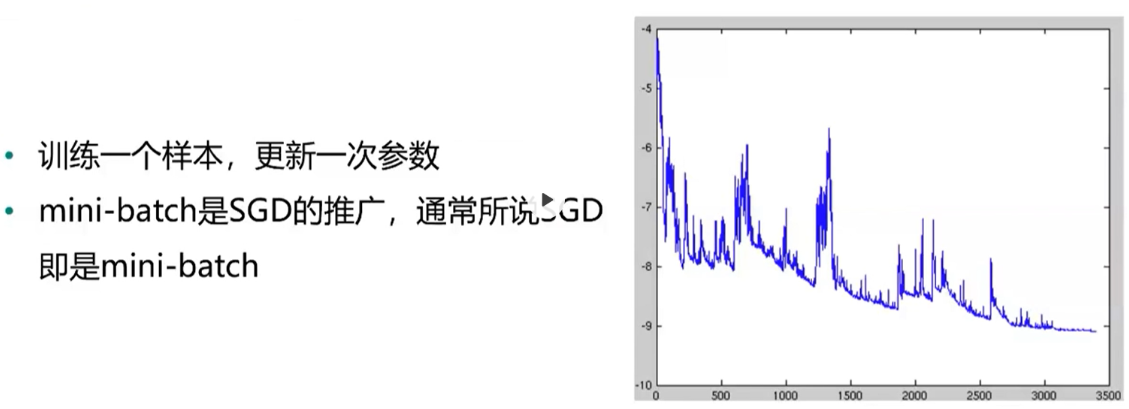
2、随机梯度下降(SGD) 沿着斜坡向下走 在实际引用中,有两种处理方法 线性衰减,然后保持为常数 开始为常数,当训练误差不再变化或变化非常小时,缩小为原来的1/10或1/2
对梯度下降法的挑战
病态条件
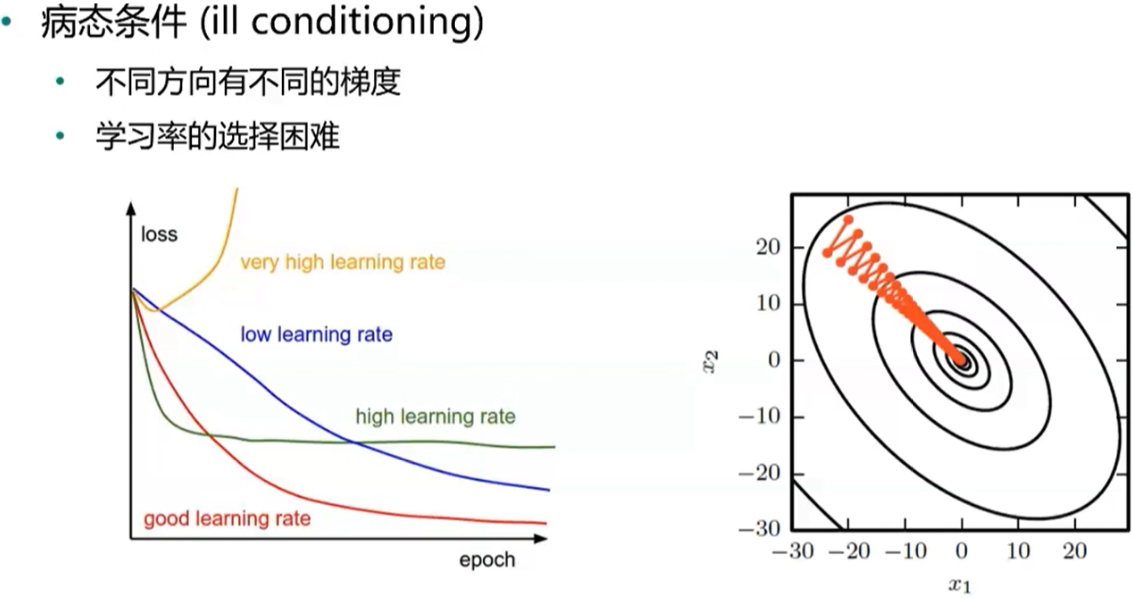
局部最小
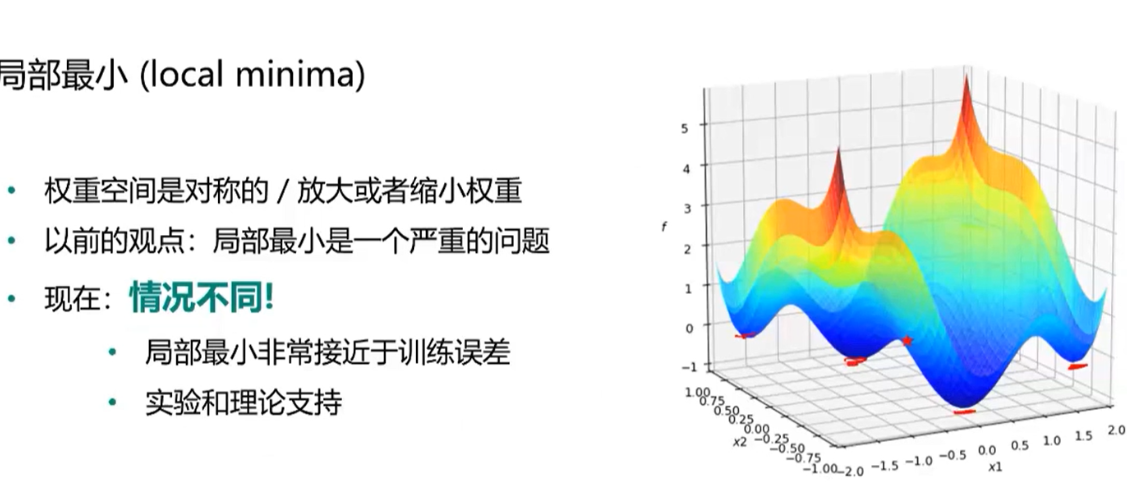
鞍点

平台

梯度爆炸与悬崖

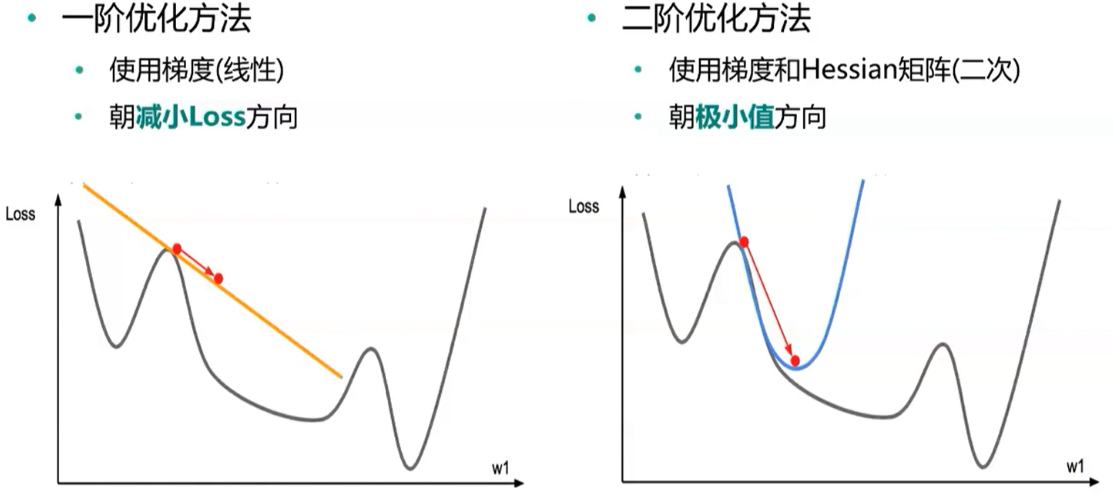
3、动量法(momentum) 主要想法:在参数更新时考虑历史梯度信息 Nesterov动量法(往前多看一步) 梯度计算在施加当前速度之后 在动量法基础上添加了一个矫正因子 4、自适应学习率方法 AdaGrad 学习率自适应:与梯度历史平方值综合的平方根成反比 效果:更为平缓的倾斜方向上会去的更大的进步,可能逃离鞍点 问题:累计梯度平方和增长过快,导致学习率迅速减小,提前终止学习 RMSProp 在AdaGrad的基础上,降低了对早起历史梯度的依赖,通过设置衰减系数β Adam 同时考虑动量和学习率自适应 5、二阶方法
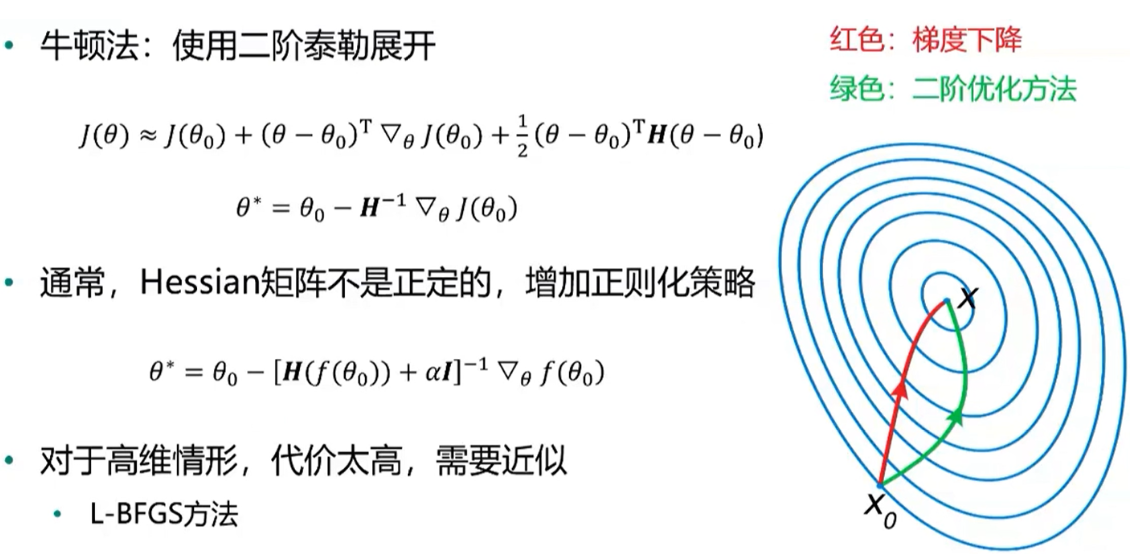
如何选择优化算法 在大数据场景(样本量大,特征维数大)下,一阶方法最实用(随机梯度) 自适应学习率算法族(以RMSProp为代表)表现相当鲁棒 Adam可能是最佳选择 使用者对算法的熟悉程度,以便于调节超参数 6、实践案例:机器学习常用优化方法的Python实践 Matplotlib:绘制三维曲面,绘制等高线,制作动画,绘制梯度场(箭头) Scipy:scipy.optimize.minimize求解最优化问题 TensorFlow:构建手写数字神经网络模型 Pandas:数据预处理,OneHot编码