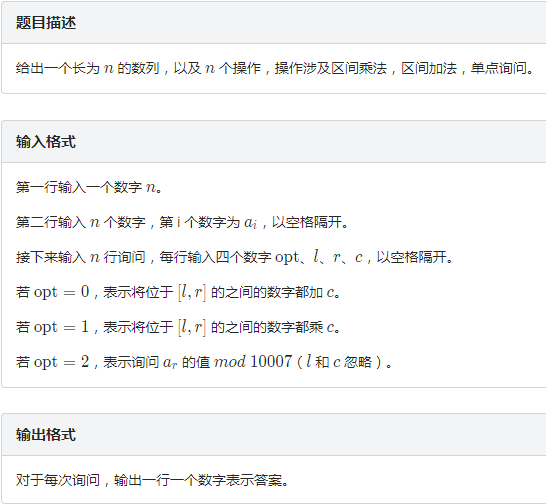
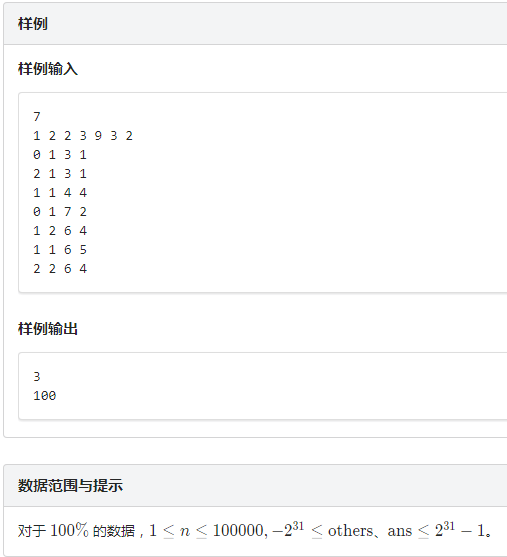
LibreOJ 6283 数列分块入门 7(区间加区间乘区间求和)

题解:这道题要打一个乘标记一个加标记,两个标记的优先级是乘法高,所以在乘的时候要将加标记同时乘上一个c,当然,对于每个非完整块一定要记得暴力重构整个块,把加标记和乘标记都初始化.

代码如下:

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define mod 10007
using namespace std;

int tag1[100010],tag2[100010],lump[100010],a[100010];
int n,sz;

void reset(int x)
{
    for(int i=(x-1)*sz+1;i<=min(x*sz,n);i++)
    {
        a[i]=(a[i]*tag2[x]+tag1[x])%mod;
    }
    tag1[x]=0;
    tag2[x]=1;
}

void add(int l,int r,int c)
{
    reset(lump[l]);
    for(int i=l;i<=min(lump[l]*sz,r);i++)
    {
        a[i]+=c;
        a[i]%=mod;
    }
    if(lump[l]!=lump[r])
    {
        reset(lump[r]);
        for(int i=(lump[r]-1)*sz+1;i<=r;i++)
        {
            a[i]+=c;
            a[i]%=mod;
        }
    }
    for(int i=lump[l]+1;i<=lump[r]-1;i++)
    {
        tag1[i]+=c;
        tag1[i]%=mod;
    }
}

void mul(int l,int r,int c)
{
    reset(lump[l]);
    for(int i=l;i<=min(lump[l]*sz,r);i++)
    {
        a[i]*=c;
        a[i]%=mod;
    }
    if(lump[l]!=lump[r])
    {
        reset(lump[r]);
        for(int i=(lump[r]-1)*sz+1;i<=r;i++)
        {
            a[i]*=c;
            a[i]%=mod;
        }
    }
    for(int i=lump[l]+1;i<=lump[r]-1;i++)
    {
        tag1[i]*=c;
        tag1[i]%=mod;
        tag2[i]*=c;
        tag2[i]%=mod;
    }
}

int main()
{
    int opt,l,r,c;
    scanf("%d",&n);
    sz=sqrt(n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        lump[i]=(i-1)/sz+1;
    }
    for(int i=1;i<=lump[n];i++)
    {
        tag2[i]=1;
    }
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d%d%d",&opt,&l,&r,&c);
        if(!opt)
        {
            add(l,r,c);
        }
        else
        {
            if(opt==1)
            {
                mul(l,r,c);
            }
            else
            {
                printf("%d\n",(a[r]*tag2[lump[r]]+tag1[lump[r]])%mod);
            }
        }
    }
}