LibreOJ 6280 数列分块入门 4(分块区间加区间求和)

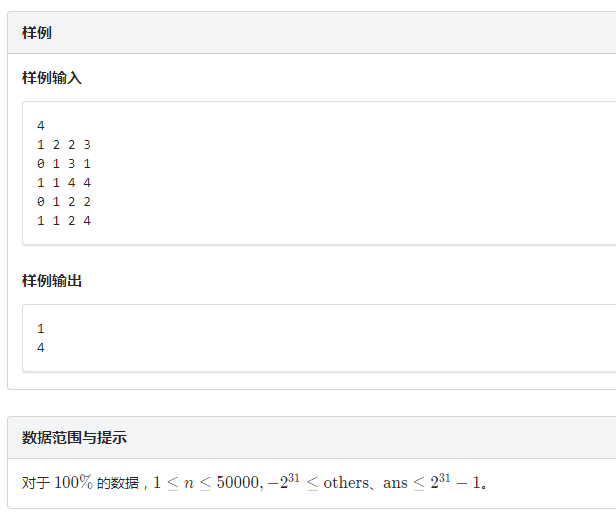
题解:分块的区间求和比起线段树来说实在是太好写了(当然,复杂度也高)但这也是没办法的事情嘛.总之50000的数据跑了75ms左右还是挺优越的.

比起单点询问来说,区间询问和也没有复杂多少,多开一个sum数组记录和,加的时候非完整块暴力重构,完整块加整块.查询时非完整块暴力加,完整块加整块

代码如下:

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

long long a[100010],sum[100010],lump[100010],tag[100010];
int n,sz;

void reset(int x)
{
    sum[x]=0;
    for(int i=(x-1)*sz+1;i<=min(sz*x,n);i++)
    {
        sum[x]+=a[i];
    }
}

void add(long long l,long long r,long long c)
{
    for(int i=l;i<=min(lump[l]*sz,r);i++)
    {
        a[i]+=c;
    }
    reset(lump[l]);
    if(lump[l]!=lump[r])
    {
        for(int i=(lump[r]-1)*sz+1;i<=r;i++)
        {
            a[i]+=c;
        }
        reset(lump[r]);
    }
    for(int i=lump[l]+1;i<=lump[r]-1;i++)
    {
        tag[i]+=c;
    }
}

long long query(long long l,long long r)
{
    long long ans=0;
    for(int i=l;i<=min(lump[l]*sz,r);i++)
    {
        ans+=a[i]+tag[lump[i]];
    }
    if(lump[l]!=lump[r])
    {
        for(int i=(lump[r]-1)*sz+1;i<=r;i++)
        {
            ans+=a[i]+tag[lump[i]];
        }
    }
    for(int i=lump[l]+1;i<=lump[r]-1;i++)
    {
        ans+=sum[i]+tag[i]*sz;
    }
    return ans;
}

int main()
{

    long long opt,l,r,c;
    scanf("%d",&n);
    sz=sqrt(n);
    for(int i=1;i<=n;i++)
    {
        scanf("%lld",&a[i]);
        lump[i]=(i-1)/sz+1;            
    }
    for(int i=1;i<=n;i++)
    {
        sum[lump[i]]+=a[i];
    }
    for(int i=1;i<=n;i++)
    {
        scanf("%lld%lld%lld%lld",&opt,&l,&r,&c);
        if(!opt)
        {
            add(l,r,c);
        }
        else
        {
            long long tmp=query(l,r);
            printf("%lld\n",tmp%(c+1));
        }
    }
}