初探FFT（快速傅里叶变换）
第一次接触省选的知识点呢！zrf大佬在课堂上讲的非常清楚，但由于本蒟蒻实在太菜了，直接掉线了。今天赶紧恶补一下。
那么这篇博客将分为两块，第一块是FFT的推导和实现，第二块则是FFT在OI上的应用
因为博主是蒟蒻，难免有些写错的地方，还请各位大佬不吝指正。
目标是能够让像博主这样的蒟蒻都能学会FFT(都有耐心看完这篇博客)
一、FFT的推导与实现
1、多项式的表示
最常见的表示方式自然是系数表示
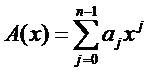
诶诶诶，别走啊，我说清楚点还不行吗？
其实就是我们常见的表达方式
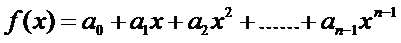
这种表达式的优势在于我们可以用O(n)的复杂度快速求值
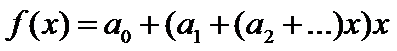
这称之为霍纳法则，很明显这是对的，因为实质上只是合并同类项。
但是遇到乘法系数表示的复杂度就不尽人意了
先等等，多项式乘法怎么乘呢？
就和一般的乘法一样列竖式计算啊！
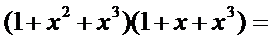
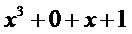
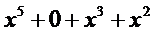
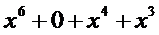
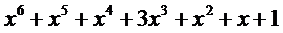
好的，我们继续说系数表示下多项式乘法的复杂度。
比如说
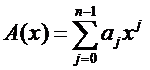
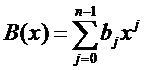
令C(x)=A(x)*B(x)，则
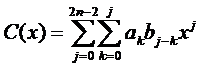
这个公式看着非常复杂，但结合上面多项式乘法的原理和定义应该可以看得懂，最重要的是，两个sigma有助于清晰直观地看出复杂度是O(n^2)的。
如果有两个长度为100000的多项式，让我们求他们的乘积，那么用这种方法，我们只好说一句“告辞”了。
但如果一定要你求呢？虽然好像强人所难，但这仍然是可做的。
“当手里的每一张牌都是坏牌，想要赢一把的唯一办法就是打破游戏规则。”--保罗·奥斯特《幻影书》《作文素材》
是的，我们发现系数表示已经阻碍住了我们的步伐，所以我们不得不舍弃它，使用一种新的表示方式--点值表示
什么是点值表示？
来来来，先一起迷糊一下：
一个次数界为n的多项式A(x)的点值表示就是一个由n个点值所组成的集合
{(x0,y0),(x1,y1),...,(xn-1,yn-1)}
对k=0,1,2...n-1，xk各不相同，yk=A(xk)
什么，你居然看懂了，好吧，我真是太菜了。
意思就是对于多项式函数，我们将n个不同的值代入该函数（n是指该多项式的最高次），将代入值与所得值组成一对，总共n对，来表示该函数。
比如说
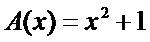
我们代入0,1,2（当然，你要代什么198,328,648或者233,666,19260817之类的也没人拦你）
则可以得出该函数的点值表示
{(0,1),(1,2),(2,5)}
好的，那么点值表示有什么优点呢？
假设
A(x)={(x0,y0),(x1,y1),...,(xn-1,yn-1)}
B(x)={(x0,g0),(x1,g1),...,(xn-1,gn-1)}
C(x)=A(x)*B(x)
噫，我记得A(x0)不就等于y0,B(x0)不就等于g0吗？
因此
C(x0)=A(x0)*B(x0)=y0*g0
所以C的点值表达式是什么呢？
C(x)={(x0,y0*g0),(x1,y1*g1),...,(xn-1,yn-1*gn-1)}
复杂度竟然是惊人的O(n)!
可优越了！
但是不得不泼一盆冷水，没有题目会选择给出点值表达的多项式，然后让你也还给他点值表达的多项式，而且就算给了，两个多项式的x也不会都是分别相等的。
所以你不得不把读进来的系数表达式转换成点值，再在乘完以后把点值转换回系数。
这样问题就来了，点值表达式真的只对应一个系数表达式吗？
首先我们先来介绍一个高科技的术语：插值
其实在这里插值什么的并不高深，可以理解为将一个多项式从点值表示转换成系数表示。
然后就要来证明插值多项式的唯一性（点值表达式只对应一个系数表达式）了
用系数的方式表示y0如下
y0=a0+a1x1+a2x1^2+...+an-1x^n-1
然后你可以用矩阵乘法来表示y0
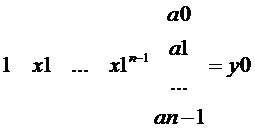
接着我们可以把y1,y2,y3.....全部代进去，放到一块
就会成这样。
左边这个矩阵在各种矩阵中是特殊的存在，被称之为范德蒙德矩阵
他的行列式值det(A)为
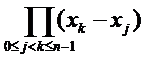
因为之前保证了xk各不相同，所以只要j不等于k，xk-xj一定不等于0
即det(A)不等于0
同时我们知道，如果有一个矩阵他没有逆矩阵，他的det一定为0
所以这个矩阵一定有逆矩阵。
有逆矩阵代表着由唯一的矩阵使
即有唯一的a
所以在对k=0,1,2...n-1，xk各不相同的情况下，插值多项式具有唯一性。
证毕了，但是结束了吗？
真遗憾并非如此，我们知道用求x所对应的点值复杂度是O(n),然后要算n个值，复杂度是O(n^2)，所以还是gg的！
那你还说用点值表示是优越的？！
先别激动，我们可以通过巧妙选取x的方式来优化这个算值的过程，使得复杂度成为O(nlogn)。
且听我慢慢道来。
首先我们需要引入一个概念
单位复数根
n次单位复数根是指一个复数ω，满足
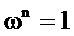
那么我们可以做以下推断：
所以n次单位根的解只有n个。
我们将n次复数根的第m个解定义为
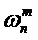其中m同样表示为
的m次方，根据上面的定义，很显然这是成立的。
所以
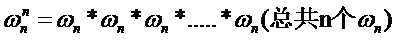
然后根据复平面上的乘法几何意义满足角度为辅角相加，长度为长度相乘的原则我们可以得出：
整个圆的度数为单位根与x轴正半轴夹角的n倍，因为单位长度所以长度没有变，角度增加如前所述
然后自然
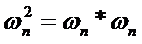
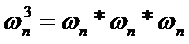
以此类推，每个单位根之间的夹角均相同，整个圆正好能排n个单位根。
即n个单位复数根均匀的分布在单位圆上。
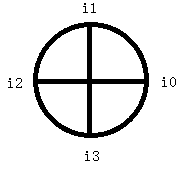
然后再给出一个知名的公式（别吓着了！这公式只是给你装逼用的！）
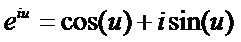
其中u是弧度制的
那么
这玩意不求理解，只是为了求值用的~当然其实在写程序的时候你会发现压根用不着e
好的，那么推了这么多，为的其实是引出几个引理（引理名称以及定义均来自于《算法导论》）。
消去引理：
对于任何整数n≥0，k≥0，以及d＞0满足
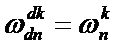
看着很高大上，但其实很简单
请问下图两条边有什么区别？
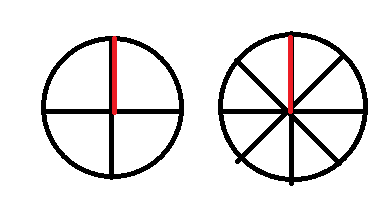
肯定没区别的啦！
就跟1/4=2/8一个道理啊。
从而可以推出
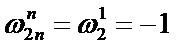
折半引理：
如果n>0，那么2n个2n次单位复数根的平方的集合就是n个n次单位复数根的集合。
这可以从感官上来证明，
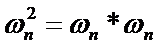
那么平方完以后就相当于辅角扩大到原来的两倍。
所以左边的就膨胀成了右边的。
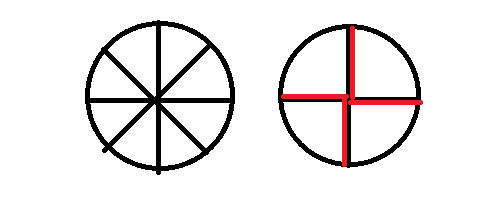
是的，如我们所见，获得每个单位根正好两次。
也就是（这个非常重要！）
然后
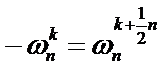
求和引理：
对于任意整数n≥1和不能被n整除的非负整数k，有（这个也很重要！）
这是怎么证的呢？
sigma看着有点难受，我们把它拆开来。
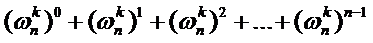
这不是一个等比序列吗？
来来来，为您送上等比数列的求和公式
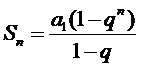
那么代入上式得：
那么如果k能被n整除呢？
DFT
好的，上面的引理都整出来了，我们开始找回我们很早很早之前提到的多项式的系数表示法
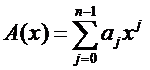
假设我们已经知道了所有的aj（废话，不知道还做什么题啊！别忘了出题人给你的是系数表示法，然后我们要求点值表示法（滑稽））
然后我们根据之前的乘法，我们需要2n个点值，以保证获得唯一插值的C
将我们已知的值
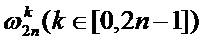
代入A(x)得
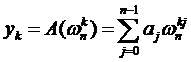
然后向量yk={y0,y1,y2...}就是向量a{a0,a1,a2...}的离散傅里叶变换（DFT），恭喜你get到了一个新的可以装逼的专业术语了！
我们记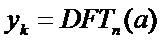
由此我们终于能够引出FFT了！
FFT
假设我们有函数
我们可以把它拆成两半
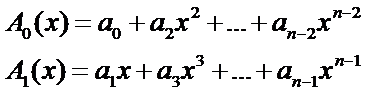
然后我们合并一下公因数
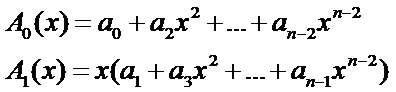
那么原式可表示为
这似乎还不够明显，让我们再设两个公式
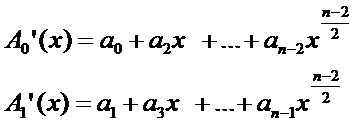
然后不是非常明显了吗？
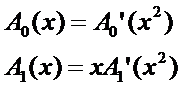
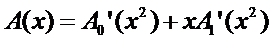
这有什么用呢？
还记得折半引理吗？
然后我们只需要知道等号右边那个玩意的值，我们就可以搞定左边的了！
然后这就是整个FFT最巧妙的一步！
原式被化成了这个样子：
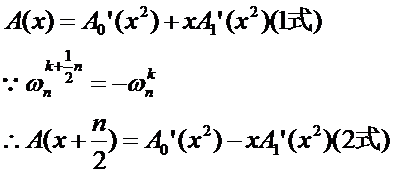
用n/2的数据可以求出n个值，这就相当于缩小了一半的大小！
所以复杂度就变成了O(nlogn)!
当然，n必须是2的幂次，如果数量不够的话，必须往高项补零！
这样就可以写出代码了：
先别得意的太早！我们只是找到了将系数表示法通过快速求值变成点值表示法的方式，然后，应该怎么把点值表示法快速插值成系数表示法呢？
IDFT&IFFT
我们曾经用范德蒙德矩阵证明过插值唯一性，在那里我们有得到过这个玩意：
只需要给已知点值乘上一个范德蒙德矩阵的逆矩阵即可
那么现在我们的范德蒙德矩阵是什么样的呢？
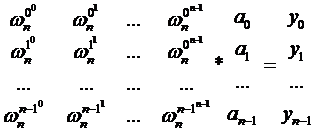
我们把这个矩阵单独拎出来
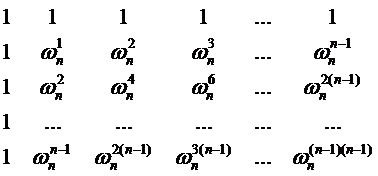
这个矩阵我们略微找下规律
j行k列的值V(j,k)为：
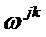
那这个范德蒙德矩阵的逆矩阵是什么？
哦，对了，逆矩阵的定义
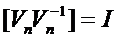
然后I是单位矩阵，长这样：
只有i行i列的值为1，其他都为0
定理30.7
对j,k=0,1,...,n-1,此逆矩阵的(j,k)处元素为
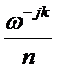
这个定理其实规定了逆矩阵长这样。
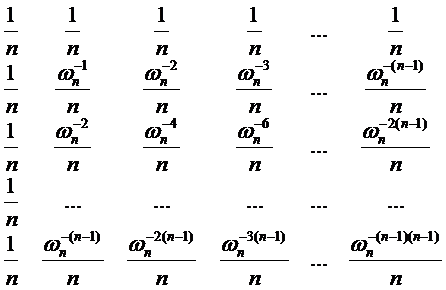
怎么证？
我们先把求和引理拖下来
对于任意整数n≥1和不能被n整除的非负整数k，有
那么范德蒙德矩阵与我们刚刚所设的矩阵的乘积的(j1,j2)处是多少呢？
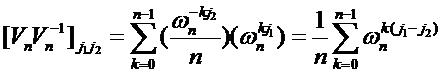
很明显，因为j1,j2=0,1,...,n-1
所以
显然
很明显范德蒙德矩阵与我们刚刚所设的矩阵的乘积就是一个单位矩阵
我们将逆矩阵代入公式，就得到了IDFT
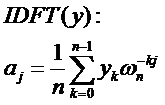
这玩意和DFT很像不是吗？
然后你可别问我
怎么求……
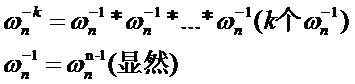
所以发现了吗？
DFT是顺时针旋转，那么IDFT就是逆时针旋转。
那么只需要在FFT上改动很小一点
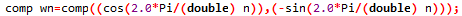
把初始的Y坐标从正翻成负的，那么就搞定了！
别忘了我们的1/n！IFFT在最后还要将结果都除以n！
那么IFFT的代码也就出来了。
既然这么像，不如整合一下，用一个kd函数表示DFT还是IDFT，如果kd为1，则做DFT，为-1做IDFT。
由此我们得到了递归版的FFT
那么多项式乘法的nlogn做法就写出来了！
代码如下：（递归版）
#include<cmath> #include<vector> #include<cstdio> #include<cstring> #include<iostream> #include<complex> #include<complex.h> #include<algorithm> #define hi puts("hi!"); using namespace std; double Pi=acos(-1.0); struct comp { double r,i; comp(){r=0,i=0;} comp(double a,double b):r(a),i(b){}; void print() { printf("%.12lf %.12lf\n",r,i); } }; inline comp operator +(const comp a,const comp b) { return comp(a.r+b.r,a.i+b.i); } inline comp operator -(const comp a,const comp b) { return comp(a.r-b.r,a.i-b.i); } inline comp operator *(const comp a,const comp b) { return comp(a.r*b.r-a.i*b.i,a.i*b.r+b.i*a.r); } int e,m; vector<comp>x,y; vector<comp> DFT(vector<comp>a,int kd) //disastrous fatal TLE { int n=a.size(); if(n==1) { return a; //Èç¹ûֻʣÏÂÒ»¸öÊý£¬ÄÇô¾ÍÖ±½Ó·µ»ØaÊý×é } vector<comp> a0,a1,y0,y1,ans; for(int i=0;i<n;i++) { if(i&1) { a1.push_back(a[i]); //ÆæÊýÏî·Öµ½a1Êý×é } else { a0.push_back(a[i]); //żÊýÏî·Öµ½a0Êý×é } } y0=DFT(a0,kd); y1=DFT(a1,kd); //·ÖÖÎ comp wn=comp((cos(2.0*Pi/(double) n)),(kd*sin(2.0*Pi/(double) n))); //Çó³öÒ»¸ön´Îµ¥Î»¸´Êý¸ùµÄÖµ comp w=comp(1.0,0.0); //¶¨ÒåµÚ0¸öµ¥Î»¸´Êý¸ùµÄÖµ ans.resize(a.size()); for(int i=0;i<n/2;i++,w=w*wn) //»ñÈ¡ÏÂÒ»¸ön´Îµ¥Î»¸´Êý¸ùµÄÖµ { ans[i]=y0[i]+y1[i]*w; //¶ÔÓ¦ÉÏÎÄһʽ ans[i+(n>>1)]=y0[i]-y1[i]*w; //¶ÔÓ¦ÉÏÎĶþʽ } return ans; } int main() { scanf("%d%d",&e,&m); for(int i=0;i<=e;i++) { int tmp; scanf("%d",&tmp); x.push_back(comp((double)tmp,0.0)); } for(int i=0;i<=m;i++) { int tmp; scanf("%d",&tmp); y.push_back(comp((double)tmp,0.0)); } int limit=1; while(limit<=e+m) { limit<<=1; } for(int i=e;i<limit-1;i++) { x.push_back(comp(0.0,0.0)); } for(int i=m;i<limit-1;i++) { y.push_back(comp(0.0,0.0)); } x=DFT(x,1); y=DFT(y,1); for(int i=0;i<limit;i++) { x[i]=x[i]*y[i]; } x=DFT(x,-1); for(int i=0;i<=e+m;i++) { printf("%d ",(int)(x[i].r/limit + 0.5)); } return 0; }
但是当我们信心满满的提交上去时，我们会发现
为什么会这样呢？
是算法错了吗？
我们去数据比较友好的loj上测试一下
这说明算法没错。
但是耗时巨久，内存开销巨大
想来也是，我们的FFT是递归版的，传递的是vector函数，不RE都奇怪啊！
那有没有方法优化呢？
有的，首先是公用子表达式上的优化。
因为复数乘法比较慢，
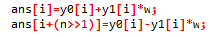
这里y1[i]*w出现了两遍，可以这么写
可惜治标不治本，它的函数传递问题还是不能解决。
不妨把它从递归版改成迭代版吧！
FFT的迭代优化
要把它从递归改成迭代的，我们需要理解它的递归结构。
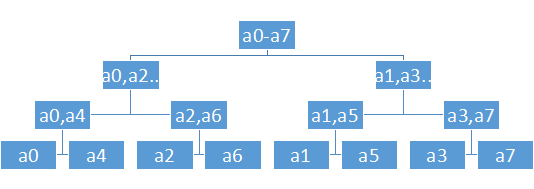
如图为8个数FFT的分治过程。
发现了吗？
没发现我们再看一下程序显示的结果
对于数据
1 2
1 2
1 2 1
第一组1 2来说
一开始我们的数组是这样的（0,1,2,3）
但是我们实际递归的顺序是（0,2,1,3）
所以递归的时候我们是按照上列排列合并的，
对于数列ans，a0是a0[0]，a4是a1[0]，并不是按照我们所理解的a0,a1
所以迭代时我们也需要按照上述格式现将数组排好。
那么怎么把原数组排成这样子呢？
找一找规律
你需要万能的二进制！
一般的数字1,2,3,4,5,6,7,8的二进制如下，如果反转一下呢？
wow！这不就是我们需要排的顺序吗？
现在的问题变成了如何快速求出i的反转数
这其实是个DP问题。
x的两倍相当于x<<1那么反转之后r[x]相当于r[x>>1]>>1
这还是好理解的，然后如果是奇数，它的末尾为一，反转之后则开头为一
于是DP公式就推出来了
r[x]=r[x>>1]>>1|(x&1)<<(l-1)
其中l是指当前情况二进制的最高位数
代码如此写：
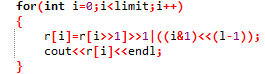
之后的操作就和递归是一样的了，一点一点的并上去。
那么最后的优化也做完了，我们可以开始写FFT的迭代版了。
再往上一提交，舒爽！
可见常数已经大大减小了，但是由于数据范围为1000000
内存占用还是很高的
但这也是没办法的事情不是吗？（容♂许之心泛滥中）
以上，本篇博客的第一部分：FFT的推导与实现终于结束了，不记公式和代码总共3600+，也挺不容易的……
然后之后就是狗尾续貂的第二部分：FFT在OI上的应用了，因为这篇博客是我边学边写的，所以应用并不高深，主要是几道例题，然后就全靠练习了……
二：FFT在OI上的应用
首先当然是我们最熟悉的多项式乘法了！
那么就先上模板吧！
多项式乘法（洛谷P3803/loj108/uoj34）
题目描述
给定一个n次多项式F(x)，和一个m次多项式G(x)。
请求出F(x)和G(x)的卷积。
输入输出格式
输入格式：
第一行2个正整数n,m。
接下来一行n+1个数字，从低到高表示F(x)的系数。
接下来一行m+1个数字，从低到高表示G(x))的系数。
输出格式：
一行n+m+1个数字，从低到高表示F(x)∗G(x)的系数。
输入输出样例
输入样例#1：
1 2
1 2
1 2 1
输出样例#1：
1 4 5 2
原理刚才已经基本上显示过了，这就是一个fft的板子
代码如下：
#include<cmath> #include<vector> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define Pi acos(-1) using namespace std; int r[4000010]; int limit,n,m,l; struct comp { double r,i; comp(){} comp(double a,double b):r(a),i(b){} void print() { printf("%.12lf %.12lf\n",r,i); } }a[4000010],b[4000010]; inline comp operator +(const comp a,const comp b) { return comp(a.r+b.r,a.i+b.i); } inline comp operator -(const comp a,const comp b) { return comp(a.r-b.r,a.i-b.i); } inline comp operator *(const comp a,const comp b) { return comp(a.r*b.r-a.i*b.i,a.i*b.r+a.r*b.i); } void FFT(comp *x,int pd) { for(int i=0;i<limit;i++) { if(i<r[i]) { swap(x[i],x[r[i]]); } } for(int mid=1;mid<limit;mid<<=1) { comp wn=comp(cos(Pi/mid),pd*sin(Pi/mid)); for(int l=mid<<1,j=0;j<limit;j+=l) { comp w=comp(1.0,0.0); for(int k=0;k<mid;k++,w=w*wn) { comp u=x[k+j]; comp v=w*x[k+j+mid]; x[k+j]=u+v; x[k+j+mid]=u-v; } } } } int main() { scanf("%d%d",&n,&m); limit=1; while(limit<=n+m) { limit<<=1; l++; } for(int i=0;i<limit;i++) { r[i]=r[i>>1]>>1|((i&1)<<(l-1)); } for(int i=0;i<=n;i++) { scanf("%lf",&a[i].r); } FFT(a,1); for(int i=0;i<=m;i++) { scanf("%lf",&b[i].r); } FFT(b,1); for(int i=0;i<limit;i++) { a[i]=a[i]*b[i]; } FFT(a,-1); for(int i=0;i<=n+m;i++) { printf("%d ",(int)(a[i].r/limit+0.5)); } return 0; }
然后我们再来一道模板题过渡一下
A*Bproblem升级版(洛谷1919/RQNOJ314/BZOJ2179)
给出两个n位10进制整数x和y，你需要计算x*y。
输入输出格式
输入格式：
第一行一个正整数n。 第二行描述一个位数为n的正整数x。 第三行描述一个位数为n的正整数y。
输出格式：
输出一行，即x*y的结果。（注意判断前导0）
输入输出样例
输入样例#1：
1
3
4
输出样例#1：
12
说明
数据范围：
n<=60000
这道题其实还是很巧妙的，把x按位数化成多项式，y也如法炮制，那么问题就变成了求多项式x与多项式y的乘积
为什么这样可以呢？
设x=23，那么转换成多项式就是{2,3}
y=24，转换成多项式就是{2,4}
两者的成绩为
{4,14,12}
这可能看不出什么，但是进下位之后呢？
{5,5,2}
那啥，23*24不就等于552吗？其实这本来就是乘法的竖式计算啊！
所以就可以用FFT锤爆了。
对于处理前导零，我选择的是从后往前做x和y的多项式
如{0,0,2,3}
这样最后的解也就自动对齐了！
代码如下：
#include<cmath> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define Pi acos(-1) using namespace std; struct comp { double r,i; comp() {} comp(double a,double b):r(a),i(b) {} } a[250010],b[250010]; inline comp operator +(const comp a,const comp b) { return comp(a.r+b.r,a.i+b.i); } inline comp operator -(const comp a,const comp b) { return comp(a.r-b.r,a.i-b.i); } inline comp operator *(const comp a,const comp b) { return comp(a.r*b.r-a.i*b.i,a.i*b.r+a.r*b.i); } int l,limit,r[250010]; void FFT(comp *x,int pd) { for(int i=0; i<limit; i++) { if(i<r[i]) { swap(x[i],x[r[i]]); } } for(int mid=1; mid<limit; mid<<=1) { comp wn=comp(cos(Pi/mid),pd*sin(Pi/mid)); for(int l=mid<<1,j=0; j<limit; j+=l) { comp w=comp(1.0,0.0); for(int k=0; k<mid; k++,w=w*wn) { comp u=x[k+j]; comp v=w*x[k+j+mid]; x[k+j]=u+v; x[k+j+mid]=u-v; } } } } int main() { char s1[100000],s2[100000]; int ans[250010],n; scanf("%d\n",&n); limit=1; while(limit<=2*n) { limit<<=1; l++; } for(int i=0; i<limit; i++) { r[i]=r[i>>1]>>1|((i&1)<<(l-1)); } gets(s1); for(int i=0; i<n; i++) { a[limit-i-1].r=s1[i]-'0'; } FFT(a,1); gets(s2); for(int i=0; i<n; i++) { b[limit-i-1].r=s2[i]-'0'; } FFT(b,1); for(int i=0; i<limit; i++) { a[i]=a[i]*b[i]; } FFT(a,-1); for(int i=0; i<=n*2; i++) { ans[i]=(int)(a[limit-i].r/limit+0.5); } int x=0; for(int i=n*2; i>=0; i--) { ans[i]+=x; x=ans[i]/10; ans[i]%=10; } int len; for(int i=0; i<=n*2; i++) { if(ans[i]) { len=i; break; } } for(int i=len; i<=n*2; i++) { printf("%d",ans[i]); } }
来道应用题：
HDU4609 3-idiots
Problem Description
King OMeGa catched three men who had been streaking in the street. Looking as idiots though, the three men insisted that it was a kind of performance art, and begged the king to free them. Out of hatred to the real idiots, the king wanted to check if they were lying. The three men were sent to the king's forest, and each of them was asked to pick a branch one after another. If the three branches they bring back can form a triangle, their math ability would save them. Otherwise, they would be sent into jail.
However, the three men were exactly idiots, and what they would do is only to pick the branches randomly. Certainly, they couldn't pick the same branch - but the one with the same length as another is available. Given the lengths of all branches in the forest, determine the probability that they would be saved.
Input
An integer T(T≤100) will exist in the first line of input, indicating the number of test cases.
Each test case begins with the number of branches N(3≤N≤105).
The following line contains N integers a_i (1≤a_i≤105), which denotes the length of each branch, respectively.
Output
Output the probability that their branches can form a triangle, in accuracy of 7 decimal places.
Sample Input
2
4
1 3 3 4
4
2 3 3 4
Sample Output
0.5000000
1.0000000
题意大致为给你n（n<=100000）根棒子，每根棒子的长度为ai（ai<=100000）
求任意取出三根能组成三角形的概率。
这道题当然是要先用O(n^3)的方法TLE一遍了！
好吧，废话不多说，我们开始怼正解（正经脸）
如果我们拿出一根长度为a[i]的棒子，假设另外两根都比它要短，那么此时我们的方案数该怎么算呢？
首先两根棒子的长度和要比a[i]长，每根的单一长度都比a[i]短。
如果我们将a数组排个序，那么a[i]之前的就都比它短了。
然后我们要取长度和大于它的
这里就可以用FFT优化了
如果把样例
4
1 3 3 4
按照长度为i的数量转化成新的数组，为：
{0,1,0,2,1}
然后组合数就是数组的卷积
什么是卷积？就是多项式的乘积啊！
比如说上面数组的卷积就是
{0,0,1,0,4,2,4,4,1}
其中的第i项就是指任取两根组成的长度个数
但其实我们把两根一样的也加起来了，所以要去掉
{0,0,0,0,4,2,2,4,0}
然后a+b和b+a我们都算了
所以答案应该再除二
{0,0,0,0,2,1,1,2,0}
接着我们会发现长度和比a[i]大的不止都是长度比它小的
然后我们要减去这些情况
第一种是取了自己的
共有n-1种
第二种是取了一个比自己大的，一个比自己小的
共有（n-i-1）*i种
第三种是取了两个都大于自己的
共有（n-i-1）*（n-i-1）/2种
然后就是O（n）的遍历跑答案了！
这道题还是很好的，完整代码如下
#include<cmath> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define Pi acos(-1) using namespace std; int n,a[400010],r[400010],l,maxx,limit; long long sum[400010],cnt[400010]; struct comp { double r,i; comp() {} comp(double a,double b):r(a),i(b) {} } num[400010]; inline comp operator +(const comp a,const comp b) { return comp(a.r+b.r,a.i+b.i); } inline comp operator -(const comp a,const comp b) { return comp(a.r-b.r,a.i-b.i); } inline comp operator *(const comp a,const comp b) { return comp(a.r*b.r-a.i*b.i,a.i*b.r+a.r*b.i); } void FFT(comp *a,int kd) { for(int i=0; i<limit; i++) { if(i<r[i]) { swap(a[i],a[r[i]]); } } for(int mid=1; mid<limit; mid<<=1) { comp wn=comp(cos(Pi/mid),kd*sin(Pi/mid)); for(int l=mid<<1,j=0; j<limit; j+=l) { comp w=comp(1.0,0.0); for(int k=0; k<mid; k++,w=w*wn) { comp u=a[k+j]; comp v=w*a[k+j+mid]; a[k+j]=u+v; a[k+j+mid]=u-v; } } } } int main() { int t; scanf("%d",&t); while(t--) { scanf("%d",&n); limit=1; l=0,maxx=0; for(int i=0; i<n; i++) { scanf("%d",&a[i]); maxx=max(maxx,a[i]); } sort(a,a+n); while(limit<=maxx*2) { limit<<=1; l++; } for(int i=0; i<limit; i++) { r[i]=r[i>>1]>>1|(i&1)<<(l-1); num[i].r=num[i].i=0.0; } for(int i=0; i<n; i++) { num[a[i]].r+=1.0; } FFT(num,1); for(int i=0; i<limit; i++) { num[i]=num[i]*num[i]; } FFT(num,-1); for(int i=0; i<limit; i++) { cnt[i]=(long long)(num[i].r/limit+0.5); } for(int i=0; i<n; i++) { cnt[a[i]<<1]--; } for(int i=0; i<limit; i++) { cnt[i]>>=1; } sum[0]=0; for(int i=1; i<limit; i++) { sum[i]=sum[i-1]+cnt[i]; } long long ans=0; for(int i=0; i<n; i++) { ans+=sum[limit-1]-sum[a[i]]; ans-=(n-1); ans-=(long long)(n-1-i)*i; ans-=(long long)(n-i-1)*(n-i-2)/2; } long long tot=(long long)n*(n-1)*(n-2)/6; printf("%.7lf\n",(double) ans/tot); } }
本来还想再多写几道题的，但是马上要省选了，实在没有时间，那就到这吧……
话说都看到这里了，那就点个推荐吧！
