POJ3020 Antenna Placement(二分图最小路径覆盖)

The Global Aerial Research Centre has been allotted the task of building the fifth generation of mobile phone nets in Sweden. The most striking reason why they got the job, is their discovery of a new, highly noise resistant, antenna. It is called 4DAir, and comes in four types. Each type can only transmit and receive signals in a direction aligned with a (slightly skewed) latitudinal and longitudinal grid, because of the interacting electromagnetic field of the earth. The four types correspond to antennas operating in the directions north, west, south, and east, respectively. Below is an example picture of places of interest, depicted by twelve small rings, and nine 4DAir antennas depicted by ellipses covering them. 
 
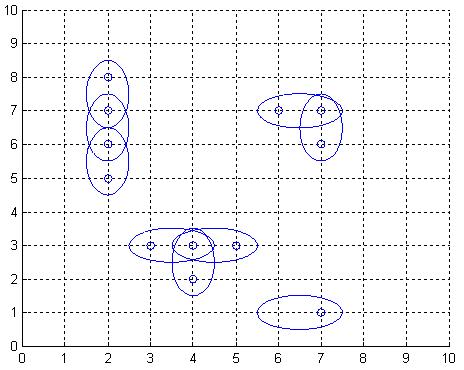
Obviously, it is desirable to use as few antennas as possible, but still provide coverage for each place of interest. We model the problem as follows: Let A be a rectangular matrix describing the surface of Sweden, where an entry of A either is a point of interest, which must be covered by at least one antenna, or empty space. Antennas can only be positioned at an entry in A. When an antenna is placed at row r and column c, this entry is considered covered, but also one of the neighbouring entries (c+1,r),(c,r+1),(c-1,r), or (c,r-1), is covered depending on the type chosen for this particular antenna. What is the least number of antennas for which there exists a placement in A such that all points of interest are covered? 

Input

On the first row of input is a single positive integer n, specifying the number of scenarios that follow. Each scenario begins with a row containing two positive integers h and w, with 1 <= h <= 40 and 0 < w <= 10. Thereafter is a matrix presented, describing the points of interest in Sweden in the form of h lines, each containing w characters from the set ['*','o']. A '*'-character symbolises a point of interest, whereas a 'o'-character represents open space. 

Output

For each scenario, output the minimum number of antennas necessary to cover all '*'-entries in the scenario's matrix, on a row of its own.

Sample Input

2
7 9
ooo**oooo
**oo*ooo*
o*oo**o**
ooooooooo
*******oo
o*o*oo*oo
*******oo
10 1
*
*
*
o
*
*
*
*
*
*

Sample Output

17
5
题意：一个n*m的平面内有一些点，有1*2的纸条，可以横放或竖放，求最少用多少张纸条才能覆盖所有点？
题解：纸条相当于一条边，上道题求得为覆盖所有边的最小点数，这道题则逆其道而行，可转化为覆盖所有点的最小边数，即最小路径覆盖
二分图中最小路径覆盖=点数-最小边覆盖
然后就可以用匈牙利跑了~
代码如下：

#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

vector<int> g[500];
int vis[500],link[500];
int map[50][20],n,m,cnt,ttt;
char c[50][20];

int dfs(int x)
{
    int sz=g[x].size();
    for(int k=0;k<sz;k++)
    {
        int y=g[x][k];
        if(!vis[y])
        {
            vis[y]=1;
            if(!link[y]||dfs(link[y]))
            {
                link[y]=x;
                return 1;
            }
        }
    }
    return 0;
}

int search()
{
    memset(link,0,sizeof(link)); 
    int tmp=0;
    for(int i=1;i<=cnt;i++)
    {
        if(dfs(i))
        {
            memset(vis,0,sizeof(vis));
            tmp++;
        }
    }
    return tmp;
}

int main()
{
    scanf("%d",&ttt);
    while(ttt--)
    {
        cnt=0;
        scanf("%d%d",&n,&m);    
        memset(map,0,sizeof(map));
        for(int i=1;i<=499;i++)
        {
            g[i].clear();
        }
        for(int i=1;i<=n;i++)
        {
            scanf("%s",c[i]);
            for(int j=0;j<m;j++)
            {
                if(c[i][j]=='o')
                {
                    map[i][j+1]=0;
                }
                else
                {
                    map[i][j+1]=++cnt;
                }
            }
        }
    
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                if(map[i][j])
                {
                    if(map[i][j+1])
                    {
                        g[map[i][j]].push_back(map[i][j+1]);
                    }
                    if(map[i][j-1])
                    {
                        g[map[i][j]].push_back(map[i][j-1]);
                    }
                    if(map[i+1][j])
                    {
                        g[map[i][j]].push_back(map[i+1][j]);
                    }
                    if(map[i-1][j])
                    {
                        g[map[i][j]].push_back(map[i-1][j]);
                    }
                }
            }
        }
        int ans=search();
        int x=cnt-ans/2;
        printf("%d\n",x);
    }
}