[公式推导]一般线性秩统计量的方差函数 及其 极限分布

秩 及 线性秩统计量的概念见参考书1的P105或参考书2的P21-P23

问题引入

参考书2-P23-定理4.1下的（4.5）式给出了线性秩统计量的方差函数

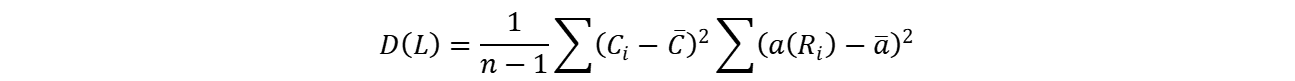
而对于Wilcoxon符号秩和统计量

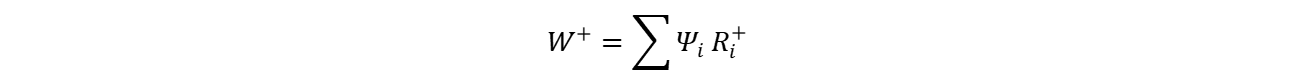
将其带入上式发现

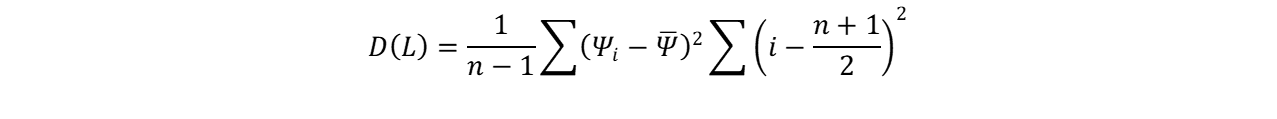
这仍然是一个随机变量，显然是与方差的性质矛盾的。

我在这个问题上思考了很久，最后决定将Wilcoxon符号秩和统计量这类的统计量定义为一般线性秩统计量，然后推导出了它的方差函数，中间遇到不少问题，但最后的结果很好，如果你也遇到同样的问题，这里或许可以帮到你。

定理1

证明

推论1

推论2

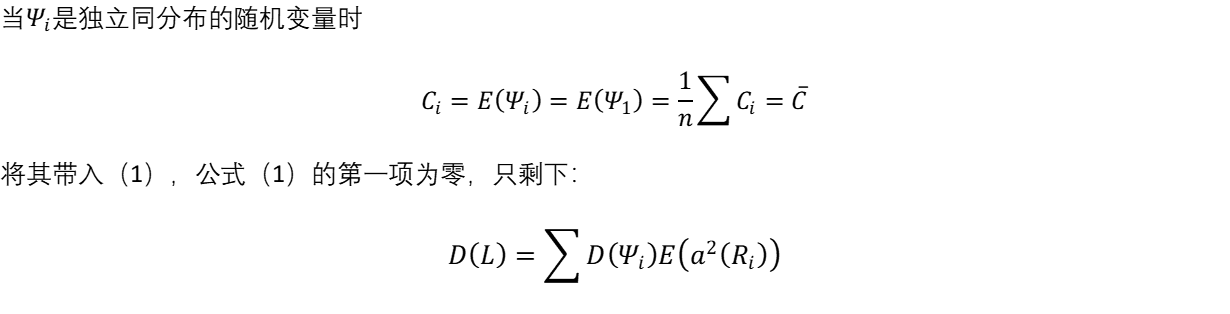
推论2应用到线性符号秩统计量中

参考书

1. 陈希孺. 非参数统计教程[M]. 华东师范大学出版社, 1993.

2. 李裕奇. 非参数统计方法[M]. 西南交通大学出版社, 2010.

posted @ 2018-06-09 21:23  司徒鲜生  阅读(1839)  评论(0)  编辑  收藏  举报