【数据结构】5.大根堆和左高树
1.大根堆
1.1 定义
大根树：树中的每一个节点的值都大于或等于其子节点的值
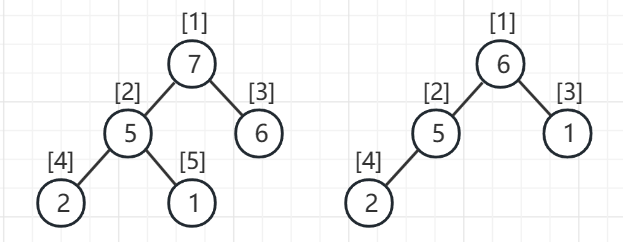
大根堆：既是大根树又是完全二叉树（增加了完全二叉树的限制条件）所以下图中只有(a)和(c)是大根堆
1.2 大根堆的插入（数组实现）
假设在下面大根堆中插入一个元素9，插入步骤如下，时间复杂度为O(height)=O(logn)
- 尝试插入在6号位置，如果新的元素小于3号位置，则插入；否则把3号位置的元素向下移动到6号位置
- 尝试插入在3号位置，如果新的元素小于1号元素，则插入；否则把1号位置的元素向下移动到3号位置，循环终止
// 为theElement寻找插入位置, currentNode从新叶子节点开始向上移动 int currentNode = ++heapSize; while (currentNode != 1 && heap[currentNode / 2] < theElement) { heap[currentNode] = heap[currentNode / 2]; // 元素向下移动 currentNode /= 2; // currentNode移动到他的双亲 } heap[currentNode] = theElement;
1.3 大根堆的出队
出队元素是最大的元素，也就是根节点，我们首先将1号元素删除，然后拿到最后一个元素，从上向下做插入的操作，时间复杂度为O(height)=O(logn)
// 从根节点开始, 为最后一个元素查找插入位置 int currentNode = 1; // 当前双亲节点 int child = 2; // 当前孩子节点 while (child <= heapSize) { // heap[child] 应该是 currentNode 更大的孩子 if (child < heapSize && heap[child] < heap[child + 1]) child++; // 对比 lastElement 是否可以插入到 currentNode if (lastElement >= heap[child]) break; // 可以插入则直接结束 // 不可以插入则继续循环 heap[currentNode] = heap[child]; // 子节点向上移动 currentNode = child; // 当前指向节点移动到子节点 child *= 2; } heap[currentNode] = lastElement;
1.4 大根堆的初始化
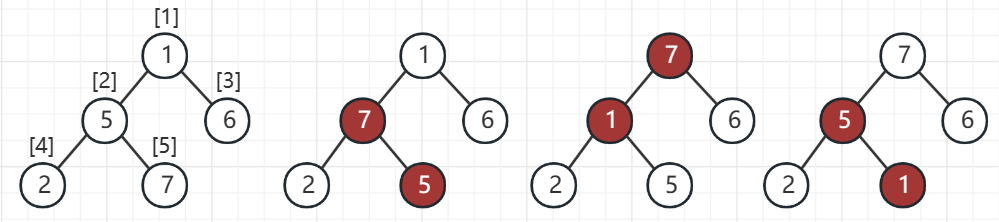
自下而上：从最后一个元素开始对比，到第一个元素结束，具体步骤如下
- ①找到孩子节点 2 和 7 中更大的元素，接下来与其双亲节点对比，7 更大所以交换 5 和 7 的位置
- ①找到孩子节点 7 和 6 中更大的元素，接下来与其双亲节点对比，7 更大所以交换 1 和 7 的位置；②找到孩子节点 2 和 5 中更大的元素，接下来与其双亲节点对比，5 更大所以交换 1 和 5 的位置
这里的循环包括两个步骤，第一个步骤是从下到上交换一次，第二个步骤是从上到下再检查一遍
// 堆化 for (int root = heapSize / 2; root >= 1; root--) { T rootElement = heap[root]; // 给元素 rootElement 寻找位置 int child = 2 * root; // 孩子 child 的双亲是 rootElement 的位置 // 确定 rootElement 的位置 while (child <= heapSize) { // heap[child] 找到孩子里更大的那一个 if (child < heapSize && heap[child] < heap[child + 1]) child++; // 是否可以把 rootElement 插入到该位置 if (rootElement >= heap[child]) break; // 可以 // 不可以 heap[child / 2] = heap[child]; // 孩子向上移动 child *= 2; // 下移一层查看 } heap[child / 2] = rootElement; }
1.5 完整代码
1.5.1 优先级队列抽象父类
#pragma once using namespace std; template<class T> class maxPriorityQueue { public: virtual ~maxPriorityQueue() {} // 队列是否为空 virtual bool empty() const = 0; // 队列大小 virtual int size() const = 0; // 返回优先级最高的元素 virtual const T& top() = 0; // 弹出优先级最高的元素 virtual void pop() = 0; // 插入元素 virtual void push(const T& theElement) = 0; };
1.5.2 大根堆的数组实现
#pragma once #include "maxPriorityQueue.h" #include <iostream> #include <algorithm> using namespace std; template<class T> class maxHeap : public maxPriorityQueue<T> { private: int heapSize; // 队列中的元素数量 int arrayLength; // 队列的容量 T* heap; // 元素数组 public: maxHeap(int initialCapacity = 10); ~maxHeap() { delete[] heap; } bool empty() const { return heapSize == 0; } int size() const { return heapSize; } const T& top() {// 返回优先级最大的元素 if (heapSize == 0) { cout << "队列为空" << endl; return NULL; } return heap[1]; } void pop(); void push(const T&); void initialize(T*, int); void deactivateArray() { heap = NULL; arrayLength = heapSize = 0; } void output() const; }; template<class T> void changeLength(T*& a, int oldLength, int newLength) {// 改变数组长度 if (newLength < 1)return; T* temp = new T[newLength]; // 新的数组 int number = min(oldLength, newLength); // 需要复制的元素个数 copy(a, a + number, temp); delete[] a; // 清理内存 a = temp; } template<class T> maxHeap<T>::maxHeap(int initialCapacity) {// 构造函数 if (initialCapacity < 1) { cout << "构造大根堆的数量必须大于1" << endl; return; } arrayLength = initialCapacity + 1; heap = new T[arrayLength]; heapSize = 0; } template<class T> void maxHeap<T>::push(const T& theElement) {// 将元素插入到大根堆 // 检查数组容量 if (heapSize == arrayLength - 1) { changeLength(heap, arrayLength, 2 * arrayLength); arrayLength *= 2; } // 为theElement寻找插入位置, currentNode从新叶子节点开始向上移动 int currentNode = ++heapSize; while (currentNode != 1 && heap[currentNode / 2] < theElement) { heap[currentNode] = heap[currentNode / 2]; // 元素向下移动 currentNode /= 2; // currentNode移动到他的双亲 } heap[currentNode] = theElement; } template<class T> void maxHeap<T>::pop() {// 从大根堆删除最大的元素 if (heapSize == 0) // 大根堆是否为空 return; // 删除最大的元素 heap[1].~T(); // 拿到最后一个元素, 并将大根堆元素数量减1 T lastElement = heap[heapSize--]; // 从根节点开始, 为最后一个元素查找插入位置 int currentNode = 1; // 当前双亲节点 int child = 2; // 当前孩子节点 while (child <= heapSize) { // heap[child] 应该是 currentNode 更大的孩子 if (child < heapSize && heap[child] < heap[child + 1]) child++; // 对比 lastElement 是否可以插入到 currentNode if (lastElement >= heap[child]) break; // 可以插入则直接结束 // 不可以插入则继续循环 heap[currentNode] = heap[child]; // 子节点向上移动 currentNode = child; // 当前指向节点移动到子节点 child *= 2; } heap[currentNode] = lastElement; } template<class T> void maxHeap<T>::initialize(T* theHeap, int theSize) {// 在数组 theHeap[1:theSize] 中初始化大根堆 delete[] heap; heap = theHeap; heapSize = theSize; // 堆化 for (int root = heapSize / 2; root >= 1; root--) { T rootElement = heap[root]; // 给元素 rootElement 寻找位置 int child = 2 * root; // 孩子 child 的双亲是 rootElement 的位置 // 确定 rootElement 的位置 while (child <= heapSize) { // heap[child] 找到孩子里更大的那一个 if (child < heapSize && heap[child] < heap[child + 1]) child++; // 是否可以把 rootElement 插入到该位置 if (rootElement >= heap[child]) break; // 可以 // 不可以 heap[child / 2] = heap[child]; // 孩子向上移动 child *= 2; // 下移一层查看 } heap[child / 2] = rootElement; } } template<class T> void maxHeap<T>::output() const { for (int i = 1; i < heapSize; i++) { cout << this->heap[i] << " "; } cout << endl; }
2.左高树
2.1 高度优先左高树和重量优先左高树
左高树合并操作的时间复杂度更低，适合需要合并操作较多的数据
定义一类特殊的节点为外部节点来代替空子树，其余节点为内部节点。增加了外部节点的二叉树称为扩充二叉树。
定义距离s：s 是该节点到外部节点的最短路径。
定义重量w：w 是该节点重量的和，节点本身重量为1，节点的重量为自身重量与孩子重量的和。
高度优先左高树（height-biased leftist tree，HBLT）：这个二叉树任何一个内部节点左孩子的 s 值都大于等于右孩子的 s 值。其中上图(a)就不是一棵左高树，因为它左侧子树的左孩子值为0，而右孩子值为1，下图是2个HBLT。
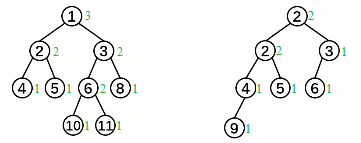
重量优先左高树（weight-biased leftist tree，WBLT）：这个二叉树任何一个内部节点左孩子的 w 值都大于或等于右孩子的 w 值。
2.2 HBLT的性质
- 堆的性质：任意节点值的大小 ≤ 其孩子节点的大小（小根堆，也可以是 ≥ ）
- 左偏性质：左孩子的距离 s ≥ 右孩子的距离 s
- 任意节点的距离 s 都等于其右孩子的距离 + 1
- 一棵有 n 个节点的二叉树，根的距离dis ≤ long(n+1) - 1（距离最远就是满二叉树的情况，否则一定有更短路径出去）
2.3 HBLT的插入和删除
插入相当于将已有的树和一棵仅有一个元素的树进行合并操作
删除相当于将左右两棵HBLT进行合并操作
2.4 HBLT的合并（链式实现）
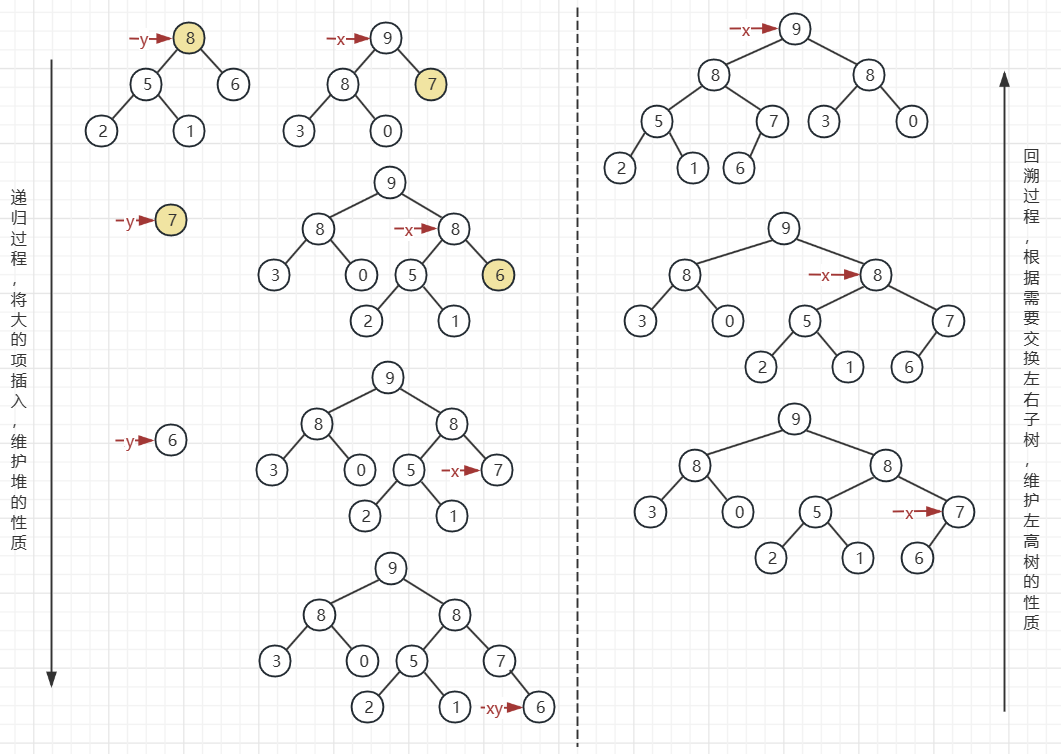
用一张图解释合并的过程，我们需要把两棵树合并到 x 上
- 对比 x 指向节点数值和 y 指向节点数值的大小
- 如果节点数值 x < y，则将 x 指向的地址和 y 指向的地址交换
- 将 x 指针移动到 x 的右孩子位置
这就是图左完整的递归过程，递归的过程实际上就是在比较两个左高树右侧孩子链的大小，并来回交换来保证堆的性质，所以整个递归应该是O(logm)+O(logn)的时间复杂度
- 首先 x 移动到下一个位置指向元素 7，对比元素 7 和元素 8，元素 8 更大，所以指针指向的地址互换，元素 8 移动到右孩子的位置
- 然后 x 移动到下一个位置指向元素 6，对比元素 6 和元素 7，元素 7 更大，所以指针指向的地址呼唤，元素 7 移动到右孩子的位置
- 然后 x 移动到下一个位置指向 NULL，因为 x 指向 NULL，所以直接将 x 指向 y 所指向的地址，递归结束
最后一步是回溯，已经完成元素的插入后，需要维护左高树的性质，回溯的过程就是根据距离不断交换孩子节点的位置，保证左孩子的距离 ≥ 右孩子的距离
template<class T> void maxHblt<T>::merged(binaryTreeNode<pair<int, T> >*& x, binaryTreeNode<pair<int, T> >*& y) {// 合并两棵左高树, x是自己的根节点地址, y是传入的根节点地址 if (y == NULL) // 如果传入的树为空, 不需要操作 return; if (x == NULL) // 如果x节点为空, 则直接让该节点的值等于传入节点的值 { x = y; return; } // 维护堆的性质, 保证 x 是更大的那一个 if (x->element.second < y->element.second) swap(x, y); // 接下来进行递归, x 向其右孩子移动一位 merged(x->rightChild, y); // 最后是回溯的过程, 需要维护左高树的性质, 保证左孩子的路径长度大于右孩子 if (x->leftChild == NULL) {// 左树为空直接交换即可 x->leftChild = x->rightChild; x->rightChild = NULL; x->element.first = 1; } else {// 左树不为空则对比他们的路径长度 if (x->leftChild->element.first < x->rightChild->element.first) swap(x->leftChild, x->rightChild); // 最后更新路径长度 x->element.first = x->rightChild->element.first + 1; } }
2.5 HBLT的初始化
template<class T> void maxHblt<T>::initialize(T* theElements, int theSize) {// 根据给定的数组初始化左高树 arrayQueue<binaryTreeNode<pair<int, T> >*> q(theSize); // 初始化树的队列 for (int i = 1; i <= theSize; i++) // 建立一个只有一个节点的树插入队列 q.push(new binaryTreeNode<pair<int, T> > (pair<int, T>(1, theElements[i]))); // 从队列中重复取出树进行合并操作 for (int i = 1; i <= theSize - 1; i++) {// 从队列中取出2个树 binaryTreeNode<pair<int, T> >* b = q.front(); q.pop(); binaryTreeNode<pair<int, T> >* c = q.front(); q.pop(); merged(b, c); // 把合并后的树插入队列 q.push(b); } if (theSize > 0) this->root = q.front(); this->treeSize = theSize; }
