【数据结构】4.二叉树

1.树

定义：一棵树 t 是一个非空有限元素的集合，其中一个元素为根（root），其余的元素组成 t 的子树（subtree）

级：树根是 1 级（level），其孩子是 2 级，孩子的孩子是 3 级

高度：高度（height）是一棵树中级的个数，也称为深度（depth）

叶子：没有孩子的元素称为叶子（leaf）

元素的度：叶子节点的个数

树的度：元素的度的最大值

2.二叉树

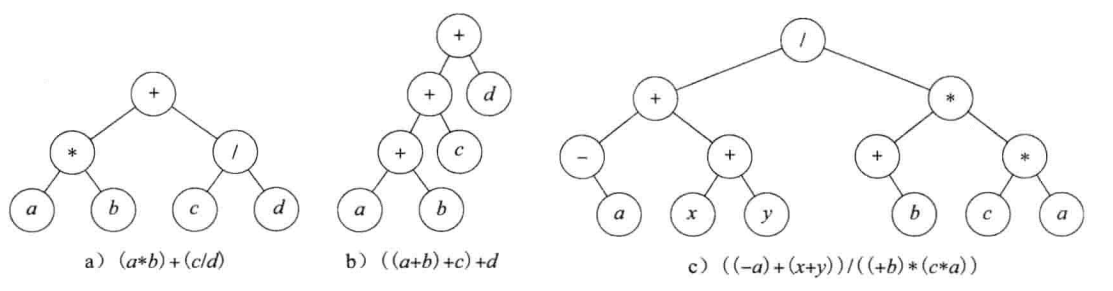
定义：二叉树（binary tree）t 是有限个元素的集合。当二叉树非空时，其中有一个元素称为根，其余元素被划分为两棵二叉树，分别称为 t 的左子树和右子树

二叉树和树的区别：

• 二叉树每个元素恰好有两科子树（其中一个或两个可能为空），树每个元素可以有任意数量的子树
• 二叉树中每个元素的子树都是有顺序的

3.二叉树的特性

1. 一棵二叉树有 n 个元素，n>0，则它有 n-1 条边（除了根节点每个元素都有一个边）
2. 一棵二叉树的高度为 h ，h≥0，则它最少有 h 个元素，最多有 2^h - 1 个元素（最少就是一条线，最多就是满的树）
3. 一棵二叉树有 n 个元素，n>0，则它的高度最大为 n，最小为 ⌈log₂(n+1)⌉
4. 一棵完全二叉树的元素编号为 i ，1 ≤ i ≤ n

　　　　4.1）如果 i=1 ，则 i 为根节点；如果i >1 ，父节点为 ⌊i/2⌋

　　　　4.2）如果 2i>n，则该元素无左孩子；如果 2i<n，则左孩子编号为 2i

　　　　4.3）如果 2i+1>n，则该元素无右孩子；如果 2i+1<n，则右孩子编号为 2i+1

二叉树：每个节点都最多有2个子节点，并且是有序的

满二叉树：高度为 h 的二叉树恰好有 2^h-1 个元素时，称为满二叉树（full binary tree)

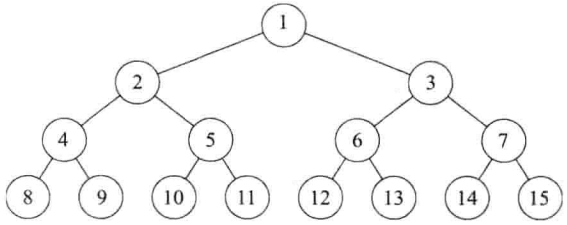
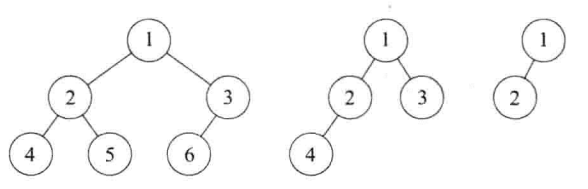
完全二叉树：一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为 i 的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

4.二叉树的描述

4.1 数组描述

在缺少元素较多的情况下，这种表述非常浪费空间，但如果是一棵完全二叉树，这种表述最有效率

4.2 链表描述

 二叉树结点结构体

#pragma once
using namespace std;

template <class T>
struct binaryTreeNode
{
    T element;
    binaryTreeNode<T>* leftChild;   // 左子树
    binaryTreeNode<T>* rightChild;  // 右子树

    binaryTreeNode() { leftChild = rightChild = NULL; }
    binaryTreeNode(const T& theElement) :element(theElement)
    {
        leftChild = rightChild = NULL;
    }
    binaryTreeNode(const T& theElement, 
        binaryTreeNode* theLeftChild, binaryTreeNode* theRightChild):element(theElement)
    {
        leftChild = theLeftChild;
        rightChild = theRightChild;
    }
};

二叉树抽象父类

#pragma once
using namespace std;

template<class T>
class binaryTree
{
public:
    virtual ~binaryTree() {}
    virtual bool empty() const = 0;
    virtual int size() const = 0;
    // 前序遍历
    virtual void preOrder() = 0;
    // 中序遍历
    virtual void inOrder() = 0;
    // 后序遍历
    virtual void postOrder() = 0;
    // 层次遍历
    virtual void levelOrder() = 0;
};

二叉树的实现

#pragma once
#include<iostream>
#include"binaryTree.h"
#include"binaryTreeNode.h"
#include<queue>
using namespace std;

template<class E>
class linkedBinaryTree : public binaryTree<binaryTreeNode<E>>
{
protected:
    binaryTreeNode<E>* root;          // 根节点指针
    int treeSize;                     // 树节点个数
public:
    // 构造函数
    linkedBinaryTree() { root = NULL; treeSize = 0; }
    // 析构函数
    ~linkedBinaryTree() { cout << "析构遍历: "; erase(); };
    // 二叉树是否为空
    bool empty() const { return treeSize == 0; }
    // 二叉树大小
    int size() const { return treeSize; }
    // 根节点
    E* rootElement() const { return treeSize == 0 ? NULL : &root->element; }
    // 制作二叉树
    void makeTree(const E& element, linkedBinaryTree<E>& left, linkedBinaryTree<E>& right);
    // 前序遍历
    void preOrder() { m_preOrder(root); }
    void m_preOrder(binaryTreeNode<E>*);
    // 中序遍历
    void inOrder() { m_inOrder(root); }
    void m_inOrder(binaryTreeNode<E>*);
    // 后序遍历
    void postOrder() { m_postOrder(root); }
    void m_postOrder(binaryTreeNode<E>*);
    // 层序遍历
    void levelOrder() { m_levelOrder(root); }
    void m_levelOrder(binaryTreeNode<E>*);
    // 树的深度
    int height() { return m_height(root); }
    int m_height(binaryTreeNode<E>*) const;
    // 释放空间
    void erase();
};

template<class E>
void linkedBinaryTree<E>::makeTree(const E& element, linkedBinaryTree<E>& left, linkedBinaryTree<E>& right)
{
    root = new binaryTreeNode<E>(element, left.root, right.root);
    treeSize = left.treeSize + right.treeSize + 1;

    left.root = right.root = NULL;
    left.treeSize = right.treeSize = 0;
}

template<class E>
void linkedBinaryTree<E>::m_preOrder(binaryTreeNode<E>* p)
{// 前序遍历
    if (p != NULL)
    {
        cout << p->element << " ";
        m_preOrder(p->leftChild);
        m_preOrder(p->rightChild);
    }
}


template<class E>
void linkedBinaryTree<E>::m_inOrder(binaryTreeNode<E>* p)
{// 中序遍历
    if (p != NULL)
    {
        m_inOrder(p->leftChild);
        cout << p->element << " ";
        m_inOrder(p->rightChild);
    }
}

template<class E>
void linkedBinaryTree<E>::m_postOrder(binaryTreeNode<E>* p)
{// 后序遍历
    if (p != NULL)
    {
        m_postOrder(p->leftChild);
        m_postOrder(p->rightChild);
        cout << p->element << " ";
    }
}

template <class E>
void linkedBinaryTree<E>::m_levelOrder(binaryTreeNode<E>* t)
{// 层序遍历
    queue<binaryTreeNode<E>*> q;
    while (t != NULL)
    {
        cout << t->element << " ";

        // 把孩子放入队列
        if (t->leftChild != NULL)
            q.push(t->leftChild);
        if (t->rightChild != NULL)
            q.push(t->rightChild);

        // 获取下一个要访问的节点
        if (q.size() == 0)
            return;
        t = q.front();
        q.pop();
    }
}

template <class E>
int linkedBinaryTree<E>::m_height(binaryTreeNode<E>* t) const
{// 返回树的高度
    if (t == NULL)
        return 0;                   // 空树
    int hl = m_height(t->leftChild);  // 左侧
    int hr = m_height(t->rightChild); // 右侧
    if (hl > hr)
        return ++hl;
    else
        return ++hr;
}

template<class E>
void linkedBinaryTree<E>::erase()
{// 删除所有节点
    binaryTreeNode<E>* p = root;
    if (p != NULL)
    {
        m_postOrder(p->leftChild);
        m_postOrder(p->rightChild);
        delete p;
    }
    root = NULL;
    treeSize = 0;
}