Hiho 1198 memory allocating algorithm
#1198 : Memory Allocating Algorithm
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
Little Hi is studying on memory allocating algorithms this summer. He starts his experiments with a very simple algorithm. By this algorithm memory is considered as a sequence of M consecutive storage units, numbered from 0 to M-1.
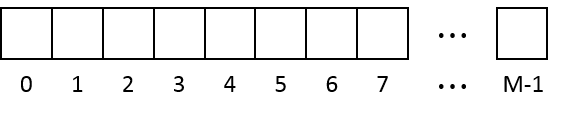
Whenever a piece of data is written to the memory the algorithm finds from 0 to M-1 the first segment of consecutive empty units which is large enough and save the data there. For example if the data size is 2 after saving it the memory look as below. Units are marked as 1 because they contain the 1st data we write.
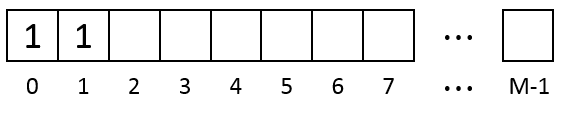
If we continue to write two pieces of data of size 3 and 2 the memory looks like below. Units 2-4 contain the 2nd data and Units 5 and 6 contain the 3rd data.

If there is not enough consecutive empty units for the coming data the algorithm will keep removing the earliest data until the coming data can be saved. Assume the memory if full after we write the 8th data:

And we need to write the 9th data of size 4. The algorithm removes the 1st data:

There is still not enough consecutive empty units so the 2nd data is also removed. Then the 9th data is saved at Units 0-3:
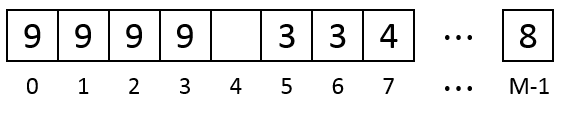
Remember if there are multiple possible segments to save the coming data the algorithm always choose the segment which is started at the unit of the smallest number.
After writing N data of different sizes Little Hi wants to know what the memory looks like.
输入
Line 1: N and M, the number of data and the size of the memory.
Line 2: N integers, K1, K2 …, KN. Ki is the size of the ith data.
For 60% of the data 1≤N≤200,10≤M≤100,1≤Ki≤5
For 100% of the data 1≤N≤2,000,10≤M≤109,1≤Ki≤M
输出
For each data which is still in the memory at last output one line of two integers id and s: the number of the data and its starting position in the memory. Output them in increasing order of id.
样例提示
The memory looks after saving each data:
1 1 1 1 1 0 0 0 0 0
1 1 1 1 1 2 2 0 0 0
1 1 1 1 1 2 2 3 3 0
4 4 0 0 0 2 2 3 3 0
4 4 5 5 5 5 0 3 3 0
4 4 5 5 5 5 6 6 6 6
样例输入
6 10 5 2 2 2 4 4
样例输出
4 0 5 2 6 6
拿到手照例看题目,第一眼看去这并不是一道很难的题目。
几个要点:
1.当内存中存在若干个可以放置的点时从最靠前的单元开始放。
2.当内存没有空间的时候删除最早放入的数据,直到放得下为止
只要满足这两个条件就可以做出题目。
但是这里有一个坑,因为样例中是完全的顺序存储,而条件一只有在倒数第二句话之前才被提到,所以看样例做题的话就很容易误会成这样的规律:
1.因为内存永远是选取最左边的为止开始放,所以只要存储最左边的空位,每次和最右边比对一下看看有没有剩余空间就好了
2.如果右边没有足够空间的话那就从左边开始删,因为永远是从左往右到底再往左,所以当右边空间不够时,最左边永远都是最小的内存块所占的区域。
当然上面这么做是错的,错误的原因只在于一种情况:
如以下输入数据:
4 5
2 2 2 1
11XXX
1122X
3322X
然后此时就会出问题,因为这种时候4号数据必然不会放入X,而是把22给踢掉以后放入。也就是说,这个破坏了上述的规律1.
于此同时,正确的做法使得id的排列不再遵守原来从左到右必然递增或者先递增再下降再递增的规律,即规律2.删除操作成为了不确定的事情,也使得对于这个想法的分类讨论这种修复方式难以实现。
那么只能想有无其他方法能实现,既然对于一组数据来说插入的位置不能以常数时间来查询,那么只能在数组里查询有无长度大于等于它的空内存块。若存在,则存入,并抛入查询队列。若不存在,则查询之前的队列,找出队列头,即最早的数据,然后在数组中定位并删除,然后在进行查询空内存块操作。
我在代码中对于每个内存块定义了开头和结尾,开头为该数据开始覆盖的位置,覆盖到结尾的前一个内存单位。一开始插入开头,其end为0,插入结尾,其sta为内存容量,这样就方便了初始化,接下来按照上文的正确规律予以实现即可。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <sstream>
#include <string>
#include <algorithm>
#include <list>
#include <map>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
#include <cstdlib>
#include<climits>
#define MAX 100005
#define ll long long
using namespace std;
struct mem
{
int id;
int sta;
int end;
};
int pos = 0,cap,op;
int comp(mem a, mem b)
{
return a.id < b.id;
}
int comp2(mem a, mem b)
{
return a.sta < b.sta;
}
int main()
{
vector<mem>sto;
cin >> op >> cap;
queue<int>Q;
mem beg,end;
beg.id = -1;
beg.sta = -1;
beg.end = 0;
sto.push_back(beg);
end.id = -1;
end.sta = cap;
sto.push_back(end);
for (int i = 0; i < op; i++)
{
int len;
scanf("%d", &len);
mem temp;
temp.id = i;
int lastpos=-1;
while (1)
{
for (int i = 0; i < sto.size() - 1; i++)
{
if (sto[i + 1].sta - sto[i].end >= len)
{
lastpos = sto[i].end;
break;
}
}
if (lastpos != -1)
{
Q.push(i);
temp.sta = lastpos;
temp.end = lastpos + len;
sto.push_back(temp);
break;
}
else
{
int target = Q.front();
Q.pop();
for (int i = 0; i < sto.size(); i++)
{
if (sto[i].id == target)sto.erase(sto.begin() + i);
}
}
}
sort(sto.begin(), sto.end(), comp2);
}
sort(sto.begin(), sto.end(), comp);
for (int i = 0; i < sto.size(); i++)
{
if(sto[i].id!=-1)
printf("%d %d\n", sto[i].id + 1, sto[i].sta);
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号