砝码称重2
参考
https://blog.csdn.net/livelylittlefish/article/details/3854702
https://www.guokr.com/article/3742
http://yetanothermathprogrammingconsultant.blogspot.com/2016/03/the-weight-problem-of-bachet-de-meziriac.html
http://www2.washjeff.edu/users/mwoltermann/Dorrie/2.pdf
https://brilliant.org/discussions/thread/the-weight-problem-of-bachet-de-meziriac/
http://josmfs.net/wordpress/wp-content/uploads/2019/04/Weight-Problem-of-Bachet-190410.pdf
https://www.cnblogs.com/ttltry-air/archive/2012/08/17/2644397.html
问题:4个砝码,每个重量都是整数克,总重量为40克,放在天平上可以称出1~40克的物体。求这4个砝码各多少克。
最简单的方法,穷举法,不过穷举法性能太低了,当前物品为x(x>0 x<=40),把砝码分成4个(abcd),a+b+c+d=40,n1*a+n2*b+n3*c+n4*d=x,再判断是否有n1*a+n2*b+n3*c+n4*d=(1-40),如果有,就满足。
穷举法太麻烦了,不管是笔试还是正式工作中,都不可能用这个方法。那么有没有其他的方法呢?既然这样说了,肯定是有的。这是一道经典的数学问题-德·梅齐里亚克的法码问题(The Weight Problem of Bachet de Meziriac),也叫巴协 (Bachet) 砝码,原版描述如下
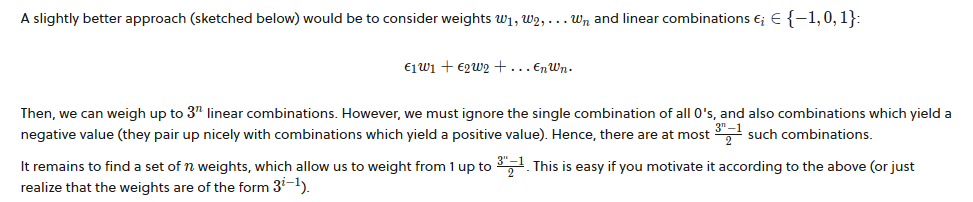
也就是一共n个砝码,每个3种状态,那么就是3*3*3...*3个排列组合,就是3^n,但是有一个0,大家都一样,所以就是3^n-1,但是由于我们不可能称重负数物品,也就是要把对称总和加起来是负数的去掉,也就是(3^n-1)/2
int main() { int num = 0; cin >> num; //(3^n-1)/2 num = num * 2 + 1; int n = 0; while (num > 1) { num = num / 3; n++; } int fmweight = 0; for (int i = 0; i < n; i++) { if (i == 0) { fmweight = 1; } else { fmweight = fmweight * 3; } cout << fmweight << " "; } char inchar; cin >> inchar; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号