数据结构与算法学习之链表(上)
链表
链表是啥
和数组属于同一中结构,都是线性表结构;但和数组不同的是,数组需要一组连续的内存空间来进行存储,而链表不需要;
链表通过指针将一组零碎的存储空间串联在一起使用,如下图所示.
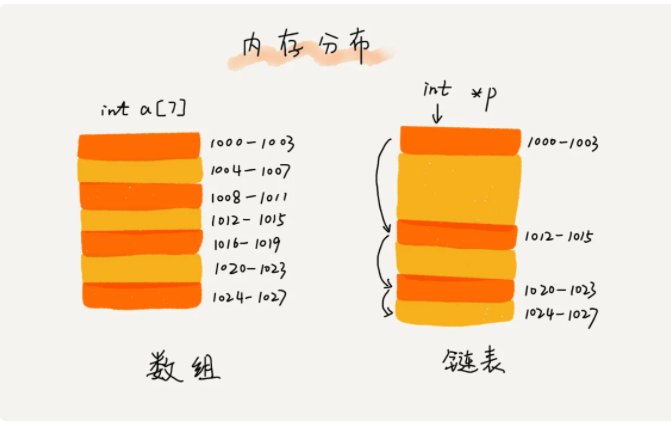
链表的类型
单链表,双向链表,循环链表,双向循环链表
链表的特性
链表的最重要的特性就是指针和结点
结点
链表通过指针将一组零散的内存块串联在一起。其中,我们把内存块称为链表的结点
指针
单链表 : 只有一个指针,叫后继指针 next ,它是为了将所有的结点串起来,每个链表的结点除了存储数据之外,还需要记录链上的下一个结点的地址,如下图所示
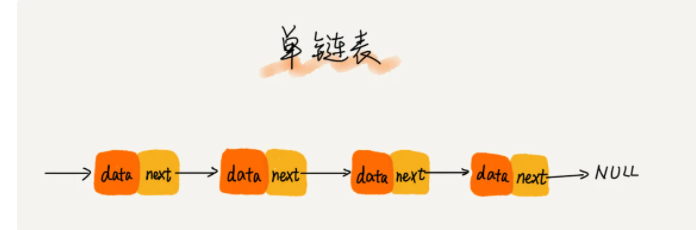
双向链表: 有两个指针,后继指针 next和前驱指针 prev,如下图所示
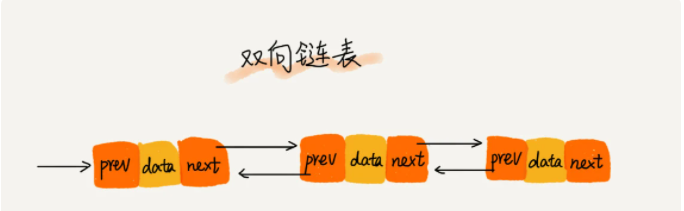
特殊的结点(单链表/双向链表)
其中有两个结点是比较特殊的,它们分别是第一个结点和最后一个结点。我们习惯性地把第一个结点叫作头结点,把最后一个结点叫作尾结点。
其中,头结点用来记录链表的基地址。
有了它,我们就可以遍历得到整条链表。
而尾结点特殊的地方是:指针不是指向下一个结点,而是指向一个空地址 NULL,表示这是链表上最后一个结点,可以看下一下单链接示意图。
特殊的结点(循环链表/双向循环链表)
循环链表的尾结点指向的是头结点,这样看起来就像一个环,如下图所示
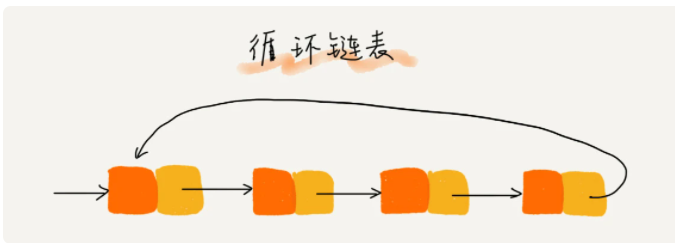
双向循环链表,如下图所示
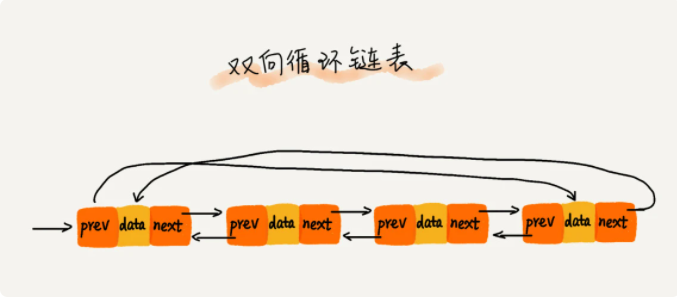
链表的操作
通过上面介绍的链表知识,也了解些链表;接下来我们学习链表的一些操作(插入,删除,查询).
插入
在进行数组的学习时候,我们也学习了数组插入的操作;
在进行插入时,如果是插入到数组尾部,则时间复杂度为O(1),并且数组需要重新迁移到一个新的连续的存储空间中;
如插入头数组的头部或者数组中间,则时间复杂度为O(n),并且数组需要重新迁移到一个新的连续的存储空间中;
链表在进行插入操作时,则不需要考虑这些
单链表
单链表在插入操作时,只需要考虑相邻的两个即可,无需迁移和扩容,时间复杂度为O(1),如下图所示
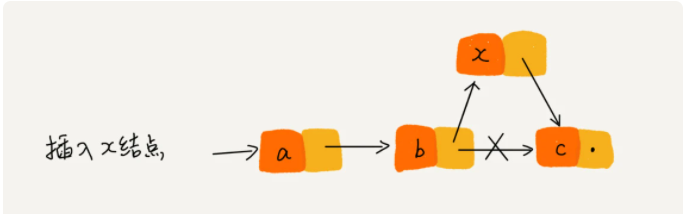
循环链表
它是特殊的单链表,在进行插入操作时,跟单链表插入一样,也只用考虑相邻的两个节点即可.
双向链表
由于双向链表有前驱指针 prev,在插入的时候,只用考虑插入地方的后一个节点即可,时间复杂度为O(1)
循环双向链表
循环双向链表的插入操作同双向链表插入操作一样
删除
在进行数组的学习时候,我们也学习了数组删除的操作;
在进行删除时,如果是删除数组尾部的数据或者数组首位数据,则时间复杂度为O(1),并且数组需要重新迁移到一个新的连续的存储空间中;
如删除数组中间的数据,则时间复杂度为O(n),并且数组需要重新迁移到一个新的连续的存储空间中;
链表在进行插入操作时,则不需要考虑这些
单链表
删除某一结点时,只需要考虑相邻的两个结点即可,如下图所示
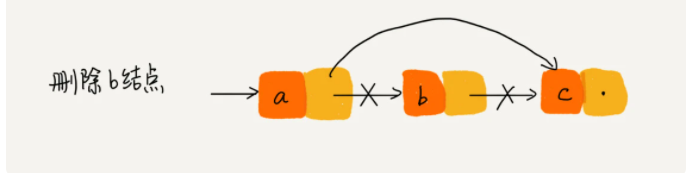
循环链表
同单链表一样
双向链表
同单链表一样
循环双向链表
同单链表一样
查询
数组的杀手锏特性就是随机访问
单链表
要进行循环才能访问到指定的结点数据
循环链表
同单链表一样
双向链表
同单链表一样
循环双向链表
同单链表一样
链表在实际开发中的注意事项(本段引自数据结构与算法之美)
以删除操作为例
在实际的软件开发中,从链表中删除一个数据无外乎这两种情况:
1.删除结点中“值等于某个给定值”的结点;
2.删除给定指针指向的结点;
第一种情况
不管是单链表还是双向链表,为了查找到值等于给定值的结点,都需要从头结点开始一个一个依次遍历对比,直到找到值等于给定值的结点,然后再通过我前面讲的指针操作将其删除。
尽管单纯的删除操作时间复杂度是 O(1),但遍历查找的时间是主要的耗时点,对应的时间复杂度为 O(n)。
根据时间复杂度分析中的加法法则,删除值等于给定值的结点对应的链表操作的总时间复杂度为 O(n)。
第二种情况
我们已经找到了要删除的结点,但是删除某个结点 q 需要知道其前驱结点,而单链表并不支持直接获取前驱结点,所以,为了找到前驱结点,我们还是要从头结点开始遍历链表,直到 p->next=q,说明 p 是 q 的前驱结点。
但是对于双向链表来说,这种情况就比较有优势了。
因为双向链表中的结点已经保存了前驱结点的指针,不需要像单链表那样遍历。
所以,针对第二种情况,单链表删除操作需要 O(n) 的时间复杂度,而双向链表只需要在 O(1) 的时间复杂度内就搞定了!
单链表与双向链表的区别
如果我们希望在链表的某个指定结点前面插入一个结点,双向链表比单链表有很大的优势。
双向链表可以在 O(1) 时间复杂度搞定,而单向链表需要 O(n) 的时间复杂度。
你可以参照我刚刚讲过的删除操作自己分析一下。
除了插入、删除操作有优势之外,对于一个有序链表,双向链表的按值查询的效率也要比单链表高一些。
因为,我们可以记录上次查找的位置p,每次查询时,根据要查找的值与p的大小关系,决定是往前还是往后查找,所以平均只需要查找一半的数据。
小结
实际上,这里有一个更加重要的知识点需要你掌握,那就是用空间换时间的设计思想。
当内存空间充足的时候,如果我们更加追求代码的执行速度,我们就可以选择空间复杂度相对较高、但时间复杂度相对很低的算法或者数据结构。
相反,如果内存比较紧缺,比如代码跑在手机或者单片机上,这个时候,就要反过来用时间换空间的设计思路。
链表与数组的性能表现
数组
数组简单易用,在实现上使用的是连续的内存空间,可以借助 CPU 的缓存机制,预读数组中的数据,所以访问效率更高。
数组的缺点是大小固定,一经声明就要占用整块连续内存空间。如果声明的数组过大,系统可能没有足够的连续内存空间分配给它,导致“内存不足(out of memory)”。
如果声明的数组过小,则可能出现不够用的情况。这时只能再申请一个更大的内存空间,把原数组拷贝进去,非常费时。
链表
而链表在内存中并不是连续存储,所以对 CPU 缓存不友好,没办法有效预读。
链表本身没有大小的限制,天然地支持动态扩容,我觉得这也是它与数组最大的区别。
数组与链表在插入,删除,查询复杂度比较
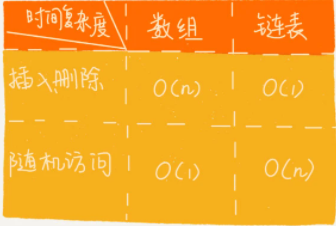
链表的应用案例
如何通过链表的方式实现LRU缓存淘汰算法
缓存
缓存是一种提高数据读取性能的技术,在硬件设计、软件开发中都有着非常广泛的应用,比如常见的 CPU 缓存、数据库缓存、浏览器缓存等等。
缓存淘汰策略
常见的策略有三种:先进先出策略 FIFO(First In,First Out)、最少使用策略 LFU(Least Frequently Used)、最近最少使用策略 LRU(Least Recently Used)。
思路
我们维护一个有序单链表,越靠近链表尾部的结点是越早之前访问的。当有一个新的数据被访问时,我们从链表头开始顺序遍历链表。
- 如果此数据之前已经被缓存在链表中了,我们遍历得到这个数据对应的结点,并将其从原来的位置删除,然后再插入到链表的头部。
- 如果此数据没有在缓存链表中,又可以分为两种情况:
- 如果此时缓存未满,则将此结点直接插入到链表的头部;
- 如果此时缓存已满,则链表尾结点删除,将新的数据结点插入链表的头部。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号