类和正则表达

正则表达式是一个很强大的字符串处理工具，它能帮助你方便的检查一个字符串是否与某种模式匹配。几乎任何关于字符串的操作都可以使用正则表达式来完成。开发者经常和字符串打交道，正则表达式更是不可或缺的技能

 

1.以下划线开头的变量名特定：

"单下划线" 开始的成员变量叫做保护变量，意思是只有类对象和自类对象自己能访问到这些变量。

"双下划线" 开始的是私有成员，意思是只有类对象自己能访问，连子类对象也不能访问到这个数据。

面向对象3要素：封装，继承和多态。

1）. 封装： 封装是把过程和数据包围起来，对数据的访问只能通过已定义的界面。面向对象计算始于这个基本概念，即现实世界可以被描绘成一系列完全自治、封装的对象，这些对象通过一个受保护的接口访问其他对象。

调用封装的内容有2种方法：

                        ——通过对象直接调用

                        ——通过self间接调用

（2）. 继承： 继承是一种联结类的层次模型，并且允许和鼓励类的重用，它提供了一种明确表述共性的方法。对象的一个新类可以从现有的类中派生，这个过程称为类继承。新类继承了原始类的特性，新类称为原始类的派生类（子类），而原始类称为新类的基类（父类）。派生类可以从它的基类那里继承方法和实例变量，并且类可以修改或增加新的方法使之更适合特殊的需要。 

注：Python的类可以继承多个类，而Java和C#中则只能继承一个类

 

Python的类如果继承了多个类，那么其寻找方法的方式有2种：

 

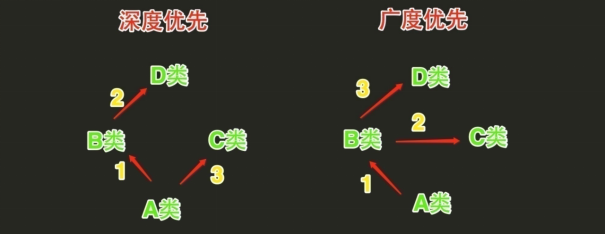
• 当类为经典类时会按照深度优先方式查找
• 

 

 

class vector3:
    def __init__(self, x_ = 0, y_ = 0, z_ = 0): #构造函数
        self.x = x_
        self.y = y_
        self.z = z_

    def __add__(self, obj):      #重载+作为加号
        return vector3(self.x+obj.x, self.y+obj.y, self.z+obj.z)

    def __sub__(self, obj):      #重载-作为减号
        return vector3(self.x-obj.x, self.y-obj.y, self.z-obj.z)

    def __mul__(self,n):         #重载*作为点乘
        return vector3(self.x*n, self.y*n, self.z*n)

    def __truediv__(self, obj):  #重载/作为除法
        return vector3(self.x/n, self.y/n, self.z/n)

    def __str__(self):
        return str(self.x)+','+str(self.y)+','+str(self.z)

if __name__ == "__main__":
    n = int(input("请输入一个标量："))
    a,b,c = map(int,input("请输入第一个向量：").split())
    v1 = vector3(a,b,c)
    a,b,c = map(int,input("请输入第二个向量：").split())
    v2 = vector3(a,b,c)
    print("两向量的加法：",v1 + v2)
    print("两向量的减法：",v1 - v2)
    print("标量与向量的乘法：",v1 * n)
    print("标量与向量的除法：",v1 / n)