2-感知机
🍧 感知机
💡 思维导图
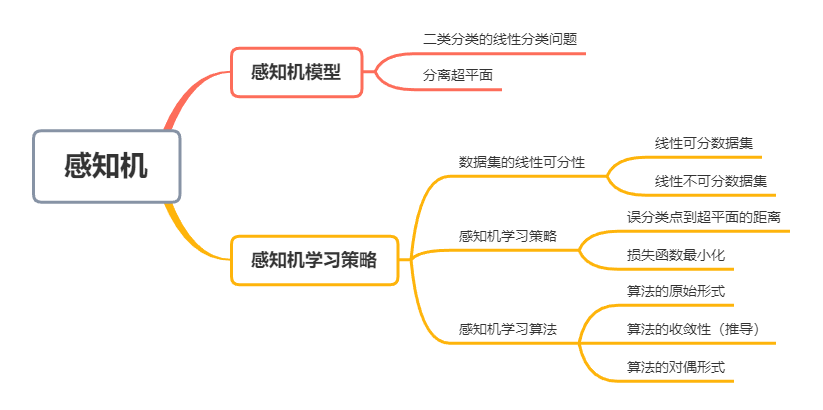
1. 感知机模型
① 概述
🔴 感知机是二类分类的线性分类模型,属于判别模型。其输入为实例的特征变量,输出为实例的类别(仅取 +1 和 -1 两个值)。
感知机预测是用学习得到的感知机模型对新的输入实例进行分类
② 定义

③ 解释
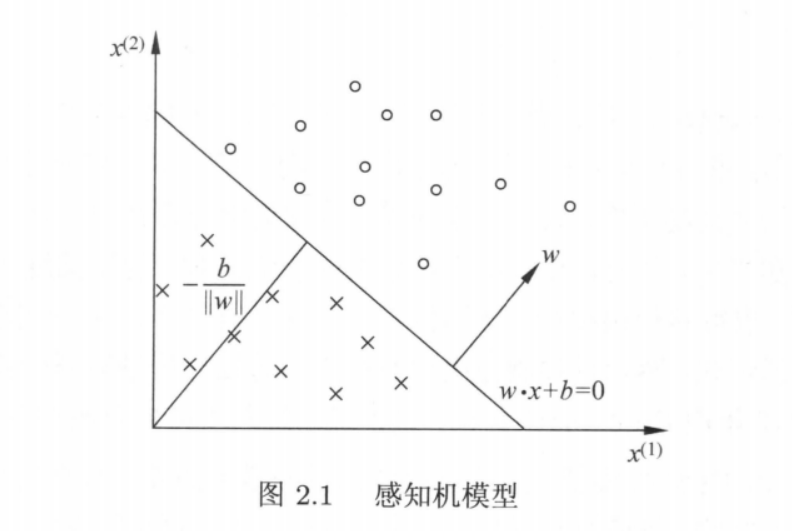
对于线性方程:$w*x + b = 0$ ,对应于特征空间中的一个超平面 S,其中 $w$ 是超平面的法向量,$b$ 是超平面的截距。
这个超平面将特征空间划分成两个部分。位于两部分的点(特征向量)分别称为正实例和负实例。因此,超平面 S 称为分离超平面 Separating Hyperplane
💡 点到直线的距离公式:
设直线 L 的方程为 $Ax+By+C=0$,点 P 的坐标为$(x_0,y_0)$,则点 P 到直线 L 的距离为:
感知学习的过程即:
由训练数据集 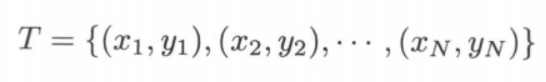 ,其中
,其中 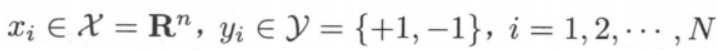 求得感知机模型(即求得模型参数 $w,b$)。对于新的输入实例,由该学习得到的感知机模型给出其对应的输出类别。
求得感知机模型(即求得模型参数 $w,b$)。对于新的输入实例,由该学习得到的感知机模型给出其对应的输出类别。
2. 感知机学习策略
① 数据集的线性可分性

💡 对于所有 $y_i = +1$ 的数据点来说, $wx_i +b > 0$ ;对于所有 $y_i = -1$ 的数据点来说, $wx_i +b < 0$ 。则称这样的数据集为线性可分数据集。
② 损失函数
感知机学习的目标就是求出一个能够将训练集正实例点和负实例点完全正确分开的分离超平面。为了找出这样的超平面,即确定感知机模型参数 $w,b$,需要确定一个学习策略,即定义损失函数并使得损失函数最小化。
感知机所采用的损失函数是误分类点到分类超平面 S 的总距离。
输入空间中任意一点 $x_0$ 到超平面 S 的距离为: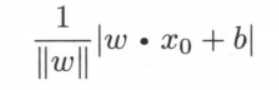
💡 上式中的 $||w||$ 是 $w$ 的 L2 范数(即向量中个元素的平方和,然后求平方根)。
L1 范数:向量中各个元素绝对值之和
L0 范数:向量中非零元素的个数
对于误分类的数据点 $(x_i,y_i)$ 来说: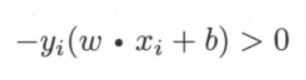
因为当 $wx_i +b > 0$ 时,错误分类点的 $y_i = -1$;当 $wx_i +b < 0$ 时,错误分类点的 $y_i = 1$
这样,所有误分类点到超平面 S 的总距离为: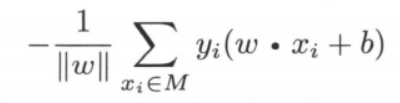
感知机的目标就是求出使得上式取得最小函数值的参数 $w,b$。显然,对于上 式的最小化问题,可以忽略常数 $\frac1{||w||}$,这样,⭐ 得出感知机 $sign(wx + b)$ 的损失函数 $L(w,b)$ 为: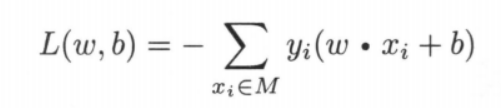 ,其中 M 为误分类点的集合。
,其中 M 为误分类点的集合。
显然,如果没有误分类点,损失函数值就是 0。误分类点越少,误分类点离超平面越近,损失函数值就越小。
🚩 感知机学习的策略就是在假设空间中选取使损失函数取得最小值时的模型参数 $w,b$
③ 感知机学习算法
感知机中求解损失函数最优化问题采用的方法是随机梯度下降法 stochastic gradient descent 👇
Ⅰ 算法的原始形式

💡 采用随机梯度下降法解决最小化问题:首先,任意选取一个超平面 $w_0,b_0$,然后用梯度下降法不断地极小化目标函数。极小化过程中不是一次性使 M 中所有误分类点的梯度下降,而是每次都随机选取一个误分类点进行梯度下降。
假设误分类点集合 M 是固定的,那么损失函数 $L(w,b)$ 的梯度由下式给出:
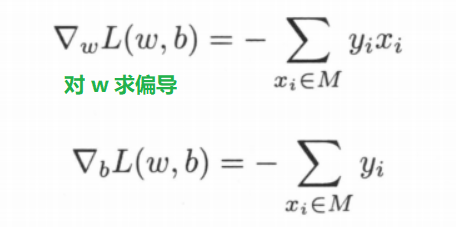

随机选取一个误分类点 $(x_i,y_i)$ 对 $w,b$ 进行更新(梯度下降):

式中 $η (0 < η ≤ 1)$ 是步长(学习率 learning rate)。
这样,通过迭代使得损失函数值不断减少,直到为 0。
⭐ 综上所述,得到感知机学习算法的原始形式如下:

💡 这种学习算法直观上的解释如下:当一个实例点被误分类(即位于分离超平面的错误一侧时),则调整 $w,b$ 的值,使分离超平面向该分类点的一侧移动,以减少该误分类点与超平面之间的距离,直至超平面越过该误分类点使其被正确分类。
💬 举个例子:
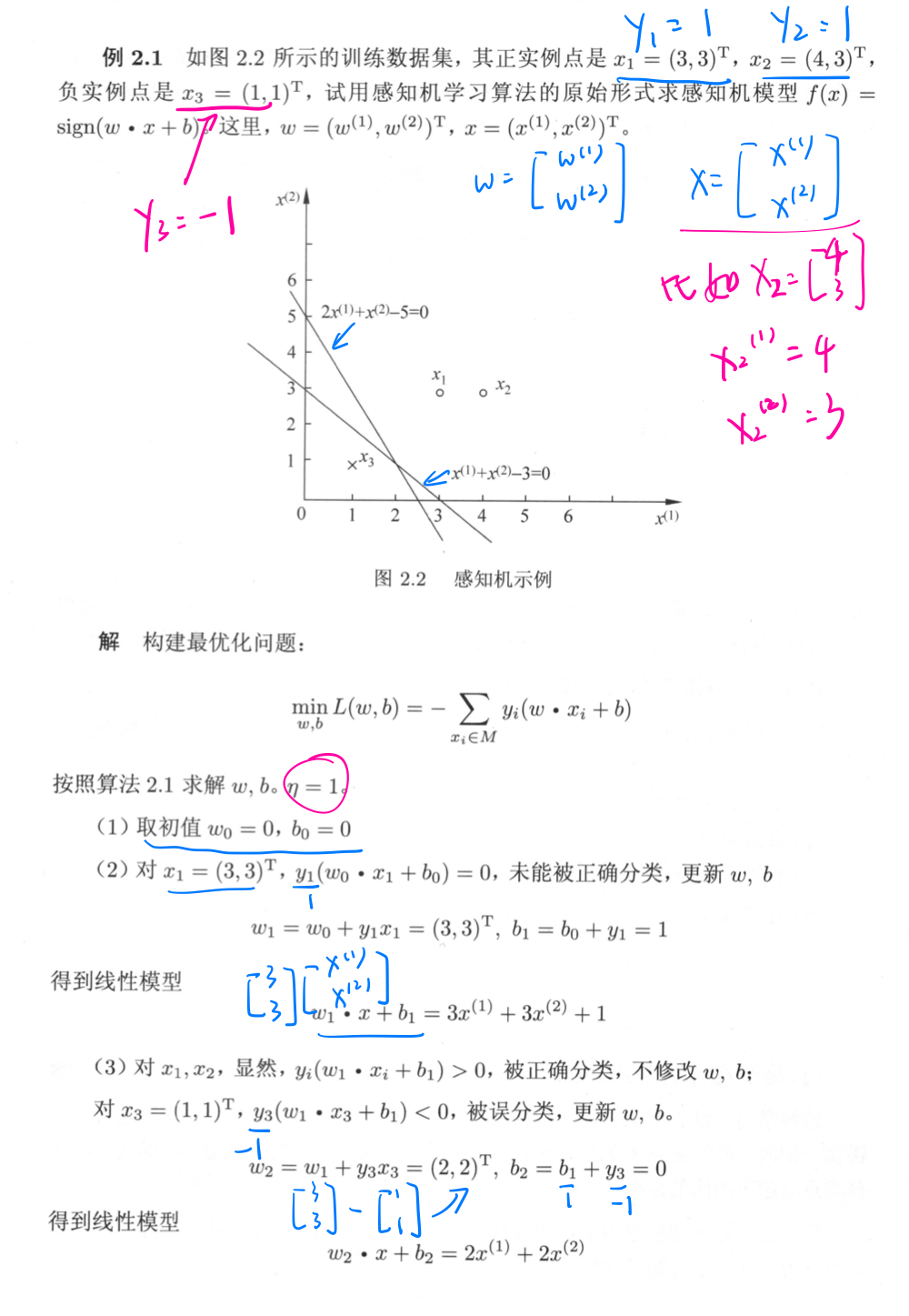
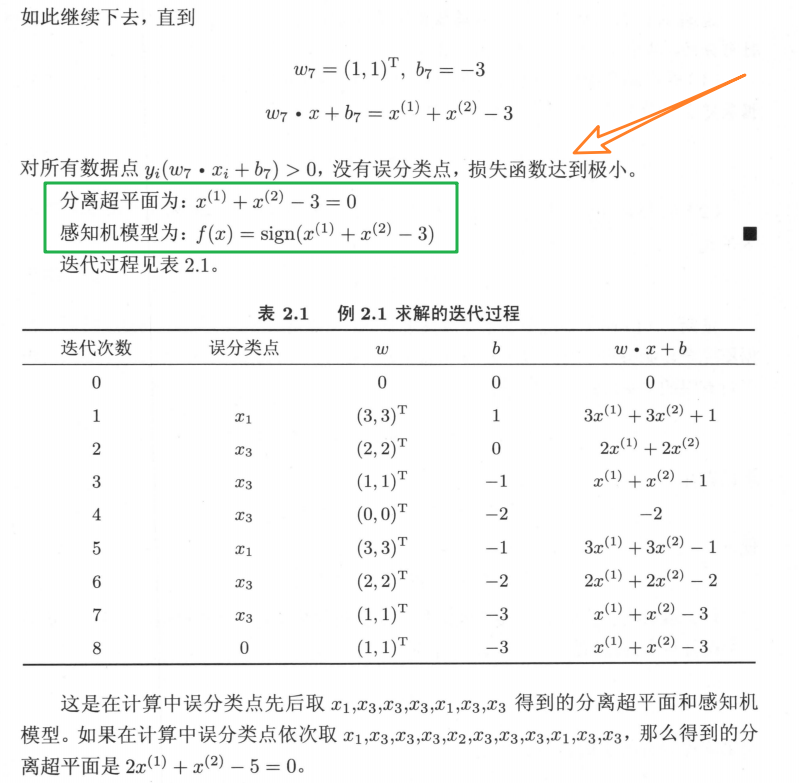
📢 由此可以看出,感知机学习算法如果采用不同的初值或选取不同的误分类点,最终结果可能不同。
Ⅱ 算法的收敛性
感知机学习算法原始形式是收敛的,即经过有限次的迭代可以得到一个将训练数据集完全正确划分的分离超平面及感知机模型。
✅ 数学推导 TODO
Ⅲ 算法的对偶形式
🔈 感知机学习算法的原始形式和对偶形式与支持向量机 SVM 算法原始形式和对偶形式相对应。
对偶形式的基本思想是:将 $w$ 和 $b$ 表示为实例 $x_i$ 和标记 $y_i$ 的线性组合形式,通过求解其系数从而求得 $w$ 和 $b$。
假设初始值 $w_0$ 和 $b_0$ 均为 0,对误分类点 $(x_i,y_i)$ 通过下式进行更新(梯度下降):
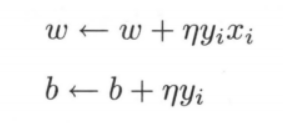
设修改 n 次,则 $w,b$ 关于 $(x_i,y_i)$ 的增量分别是 $α_iy_ix_i$ 和 $α_iy_i$,注意这里的 $α_i = n_iη$
这样,最后学习到的 $w,b$ 可以分别表示为:
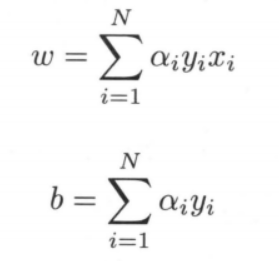
这里,$α_i ≥ 0, i = 1,2,...,N$,当 η = 1 时,$α_i$ 表示第 i 个实例点由于误分类而进行更新的次数。
实例点更新次数越多,意味着它距离分离超平面越近,也就越难正确分类。换句话说,这样的实例对学习结果影响最大。
⭐ 下面对照算法的原始形式来描述感知机学习算法的对偶形式:

注意,对偶形式中训练集中的数据点之间的运算仅以内积即 $x_i·x_j$ 出现,为了方便,可以预先将训练集中实例间的内积计算出来并以矩阵的形式存储,这个矩阵就是所谓的 Gram 矩阵:
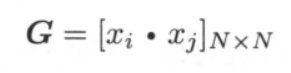
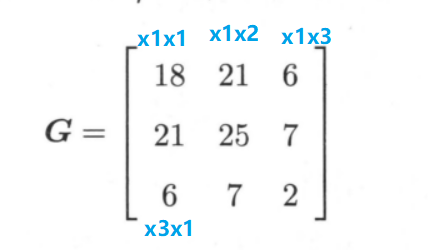
💬 比如说数据集中拥有 3 个点: $x_1 = \begin{bmatrix} 3 \ 3 \end{bmatrix}$,$x_2 = \begin{bmatrix} 4 \ 3 \end{bmatrix}$,$x_3 = \begin{bmatrix} 1 \ 1 \end{bmatrix}$,该数据集的的 Gram 矩阵就是:
关于感知机算法的对偶形式,💬 举例如下:

与原始形式一样,感知机学习算法的对偶形式也是收敛的,且由于选取初值的不同或误分类点的选取次数不同,存在多个解
📚 References
- 《统计学习方法 - 第 2 版》
- 《Machine Learning in Action》
- 《机器学习 - 周志华》
- L1范数与 L2 范数的区别

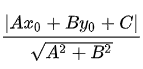

 浙公网安备 33010602011771号
浙公网安备 33010602011771号