12-利用PCA简化数据
🥡 利用 PCA 来简化数据
1. 降维技术 dimensionality
比如说我们正通过电视观看体育比赛,在电视的显示器上有一个球。显示器大概包含了100万像素点,而球则可能是由较少的像素点组成,例如说一千个像素点。
人们实时的将显示器上的百万像素转换成为一个三维图像,该图像就给出运动场上球的位置。在这个过程中,人们已经将百万像素点的数据,降至为三维。这个过程就称为 降维 dimensionality。在低维下,数据更容易处理。
有时我们会显示三维图像或者只显示其相关特征,但是数据往往拥有超出显示能力的更多特征。数据显示并非大规模特征下的唯一难题,对数据进行简化还有如下一系列的原因:
- 使得数据集更容易使用
- 降低很多算法的计算开销
- 去除噪音
- 使得结果易懂
在已标注与未标注的数据上都有降维技术。这里我们将主要关注未标注数据上的降维技术,将技术同样也可以应用于已标注的数据。
💡 降维技术使得数据变的更易使用,并且它们往往能够去除数据中的噪音,使得其他机器学习任务更加精确。降维往往作为预处理步骤,在数据应用到其他算法之前清洗数据。。
🚩 降维技术如下:
- 主成分分析(Principal Component Analysis, PCA)
- 通俗理解: 就是找出一个最主要的特征,然后进行分析。
- 例如: 考察一个人的智力情况,就直接看数学成绩就行(存在: 数学、语文、英语成绩)
- 因子分析(Factor Analysis)
- 通俗理解: 将多个实测变量转换为少数几个综合指标。它反映一种降维的思想,通过降维将相关性高的变量聚在一起,从而减少需要分析的变量的数量,而减少问题分析的复杂性`
- `例如: 考察一个人的整体情况,就直接组合3样成绩(隐变量),看平均成绩就行(存在: 数学、语文、英语成绩)
- 应用的领域: 社会科学、金融和其他领域
- 在因子分析中,我们
- 假设观察数据的成分中有一些观察不到的隐变量(latent variable)。
- 假设观察数据是这些隐变量和某些噪音的线性组合。
- 那么隐变量的数据可能比观察数据的数目少,也就说通过找到隐变量就可以实现数据的降维。
- 独立成分分析(Independ Component Analysis, ICA)
- 通俗理解: ICA 认为观测信号是若干个独立信号的线性组合,ICA 要做的是一个解混过程。`
- 例如: 我们去ktv唱歌,想辨别唱的是什么歌曲?ICA 是观察发现是原唱唱的一首歌【2个独立的声音(原唱/主唱)】。
- ICA 是假设数据是从 N 个数据源混合组成的,这一点和因子分析有些类似,这些数据源之间在统计上是相互独立的,而在 PCA 中只假设数据是不 相关(线性关系)的。
- 同因子分析一样,如果数据源的数目少于观察数据的数目,则可以实现降维过程。
在以上3种降维技术中, PCA 的应用目前最为广泛,因此本章主要关注PCA。👇
2. 主成分分析 PCA
① 移动坐标轴
PCA 的工作原理如下:
-
找出第一个主成分的方向,也就是数据
方差最大的方向。 -
找出第二个主成分的方向,也就是数据
方差次大的方向,并且该方向与第一个主成分方向正交(orthogonal 如果是二维空间就叫垂直)。💬 举例如下:
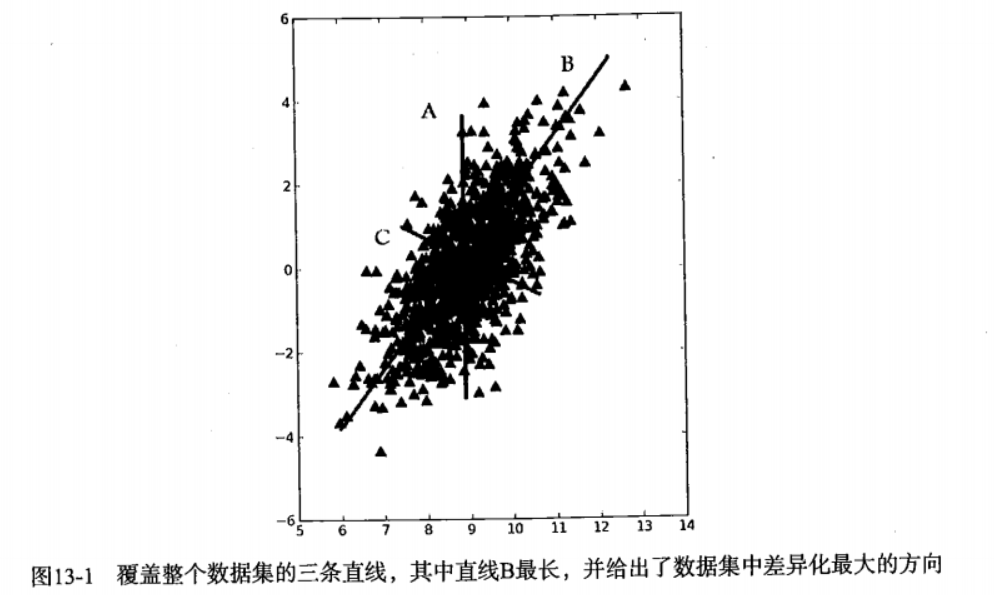
图书的直线 B 可以最大程度覆盖数据集,那么 直线 B 就是第一个主成分的方向。直线 C 垂直于 B,那么 直线 C 就是第二个主成分的方向。
-
通过这种方式计算出所有的主成分方向。
-
通过数据集的协方差矩阵及其特征值分析,我们就可以得到这些主成分的值。
方差: (一维)度量两个随机变量关系的统计量
协方差: (二维)度量各个维度偏离其均值的程度
协方差 cov = $[(x1-x{均值})(y1-y{均值})+(x2-x{均值})(y2-y{均值})+...+(xn-x{均值})*(yn-y{均值})+]/(n-1)$
- 当 $cov(X, Y)>0$ 时,表明X与Y正相关;(X越大,Y也越大;X越小Y,也越小。)
- 当 $cov(X, Y)<0$ 时,表明X与Y负相关;
- 当 $cov(X, Y)=0$ 时,表明X与Y不相关。
协方差矩阵: (多维)度量各个维度偏离其均值的程度
-
一旦得到了协方差矩阵的特征值和特征向量,我们就可以保留最大的 N 个特征。这些特征向量也给出了 N 个最重要特征的真实结构,我们就可以通过将数据乘上这 N 个特征向量 从而将它转换到新的空间上。
举例如下:
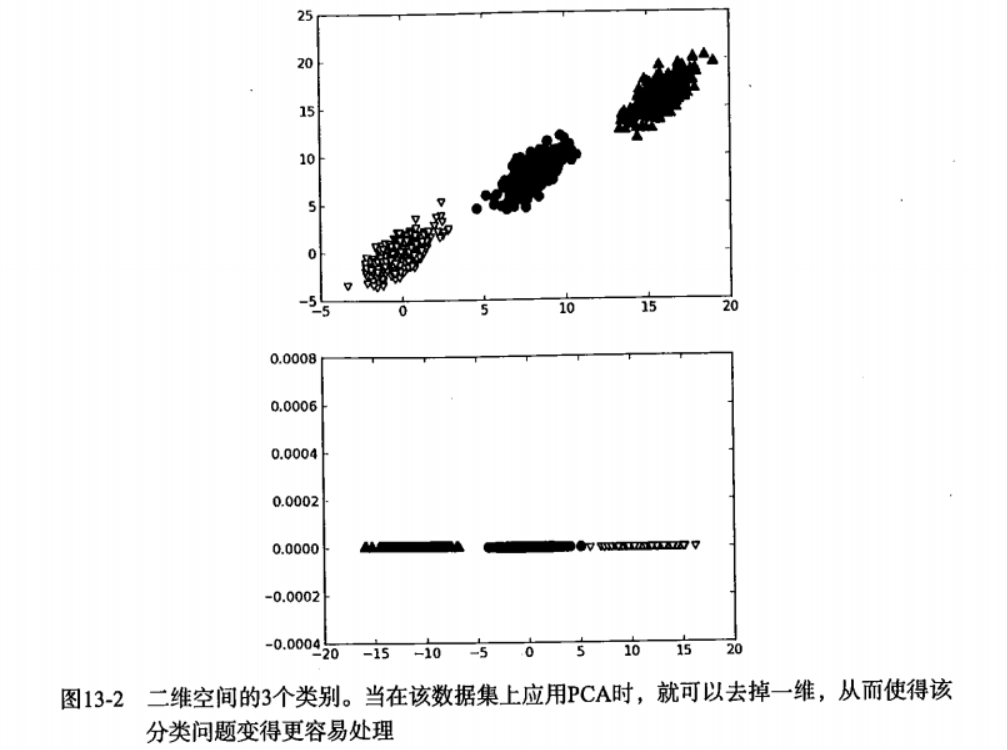
② 在 Numpy 中实现 PCA
📑 将数据转换成前 N 个主成分的伪代码如下:
去除平均值
计算协方差矩阵
计算协方差矩阵的特征值和特征向量
将特征值从大到小排序
保留最上面的 N 个特征向量
将数据转换到上述 N 个特征向量构建的新空间中
✍ Python 实现:
import numpy as np
def loadDataSet(fileName,delim='\t'):
fr = open(fileName)
stringArr = [line.strip().split(delim) for line in fr.readlines()]
dataArr = [list(map(float,line)) for line in stringArr]
return np.mat(dataArr)
def pca(dataMat,topNfeat = 9999999):
""""
Args:
dataMat 原数据集矩阵
topNfeat 应用的N个特征
Returns:
lowDDataMat 降维后数据集
reconMat 新的数据集空间
"""
meanVals = np.mean(dataMat,axis = 0) # 每列(每个特征)的平均值
meanRemoved = dataMat - meanVals # 去除平均值
covMat = np.cov(meanRemoved, rowvar=0) # 协方差矩阵
# eigVals为协方差矩阵的特征值, eigVects为特征向量
eigVals, eigVects = np.linalg.eig(np.mat(covMat))
eigValInd = np.argsort(eigVals) # 将特征值从小到大排序
# -1表示倒序,保留后面 N 个较大的特征值
eigValInd = eigValInd[:-(topNfeat+1):-1]
redEigVects = eigVects[:,eigValInd] # 保留这N个特征值对应的N个特征向量
lowDDataMat = meanRemoved * redEigVects # 降维后的数据集
reconMat = (lowDDataMat * redEigVects.T) + meanVals # 将数据转换到新空间
return lowDDataMat,reconMat
🏃 运行该代码:
dataMat = loadDataSet('testSet.txt')

对数据 进行降维:
lowDMat, = pca(dataMat,1) # 降到一维
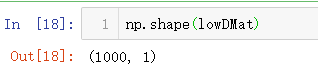
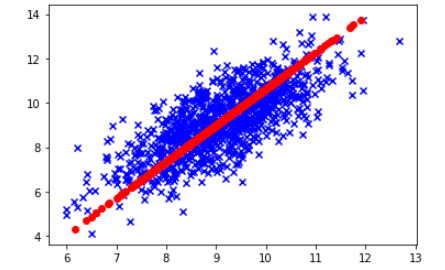
👀 对原始数据集合降维后的数据集进行可视化:
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
# 原始数据集
ax.scatter(dataMat[:,0].flatten().A[0], dataMat[:,1].flatten().A[0],marker = 'x',color='blue')
# 降维后的数据集
ax.scatter(reconMat[:,0].flatten().A[0], reconMat[:,1].flatten().A[0],marker = 'o',color='red')
plt.show()
📚 References
-
《Machine Learning in Action》



 浙公网安备 33010602011771号
浙公网安备 33010602011771号