7-线性回归
🌐 线性回归
🚀 从本节开始介绍回归方法，回归和前面章节介绍的分类方法同属于监督学习方法。
我们前边提到的分类的目标变量是标称型数据，而回归则是对连续型的数据做出处理，回归的目的是预测数值型数据的目标值。
1. 用线性回归找到最佳拟合直线
① 线性回归的概念
回归的目的是预测数值型的目标值。最直接的办法是依据输入写出一个目标值的计算公式。
假如你想要预测兰博基尼跑车的功率大小，可能会这样计算:
HorsePower = 0.0015 * annualSalary - 0.99 * hoursListeningToPublicRadio
这就是所谓的 回归方程(regression equation)，其中的 0.0015 和 -0.99 称作 回归系数（regression weights），求这些回归系数的过程就是回归。一旦有了这些回归系数，再给定输入，做预测就非常容易了。具体的做法是用回归系数乘以输入值，再将结果全部加在一起，就得到了预测值。我们这里所说的，回归系数是一个向量，输入也是向量，这些运算也就是求出二者的内积。
⭐ 说到回归，一般都是指 线性回归(linear regression)。线性回归意味着可以将输入项分别乘以一些常量，再将结果加起来得到输出。训练出一条直线最佳拟合数据集。
📜 最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。
② 线性回归工作原理
❓ 我们应该怎样从一大堆数据里求出回归方程呢？
假定输入数据存放在矩阵 X 中，而回归系数存放在向量 w 中。那么对于给定的数据 X1，预测结果将会通过 $Y = X_1^T w$ 给出。现在的问题是，手里有一些 X 和对应的 y，怎样才能找到 w 呢？
一个常用的方法就是找出使误差最小的 w 。这里的误差是指预测 y 值和真实 y 值之间的差值，使用该误差的简单累加将使得正差值和负差值相互抵消，所以我们采用平方误差函数：（实际值 - 预测值）^2（实际上就是我们通常所说的最小二乘法）。
平方误差可以写做（代价/损失函数）:
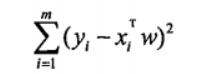
用矩阵表示还可以写做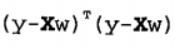 
如果对 w 求导，得到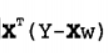 
，令其等于零，解出 w 如下（正规方程解法）：
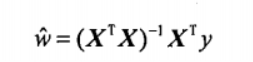
w 上方的小标记表示这是当前可以估计出的 w 的最优解。
💡 求解代价函数中回归系数 w 除了上述的正规方程法，常见的还有梯度下降法
有上述公式可知，需要对矩阵求逆，因此这个方程只在矩阵可逆的时候适用，我们在程序代码中对此作出判断。 判断矩阵是否可逆的一个可选方案是：
📜 判断矩阵的行列式是否为 0，若为 0 ，矩阵不可逆，不为 0 的话，矩阵可逆。
⭐ 由此总结出线性回归的工作原理：
- 读入数据，将数据特征 X、特征标签 y 存储在矩阵 X、y 中
- 验证 $X^TX$ 矩阵是否可逆
- 使用最小二乘法求得回归系数 w 的最佳估计
上述过程也成为标准线性回归
③ 线性回归的工作流程
- 收集数据: 采用任意方法收集数据
- 准备数据: 回归需要数值型数据，标称型数据将被转换成二值型数据
- 分析数据: 绘出数据的可视化二维图将有助于对数据做出理解和分析，在采用缩减法求得新回归系数之后，可以将新拟合线绘在图上作为对比
- 训练算法: 找到回归系数
- 测试算法: 使用代价函数（平方误差函数），分析模型的效果
- 使用算法: 使用回归，可以在给定输入的时候预测出一个数值，这是对分类方法的提升，因为这样可以预测连续型数据而不仅仅是离散的类别标签
④ 实际案例
根据下图中的点，找出该数据的最佳拟合直线。
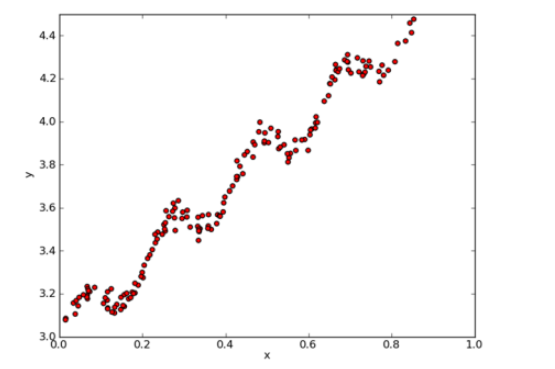
数据格式如下：
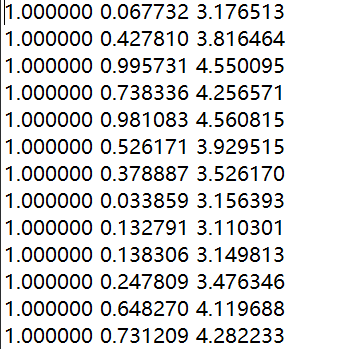
第一个特征值总是等于 1.0 即 $x_0$
✍ 数据导入函数：
def loadDataSet(fileName):
numFeat = len(open(fileName).readline().split('\t')) - 1 # 获取每行字段的个数 3
dataMat = []
labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = []
curLine = line.strip().split('\t') # 当前行数据
for i in range(numFeat):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat,labelMat
✍ 线性回归函数：
import numpy as np
def standRegres(xArr, yArr):
"""
Desc:
求出最佳 w
Args：
xArrr：特征向量
yArr： 标签向量
Return:
返回回归系数 w
"""
xMat = np.mat(xArr)
yMat = np.mat(yArr).T
xTx = xMat.T*xMat
if np.linalg.det(xTx) == 0.0: # 计算行列式
print("特征矩阵不可逆！")
return
ws = xTx.I * (xMat.T * yMat)
return ws
🏃 运行结果：
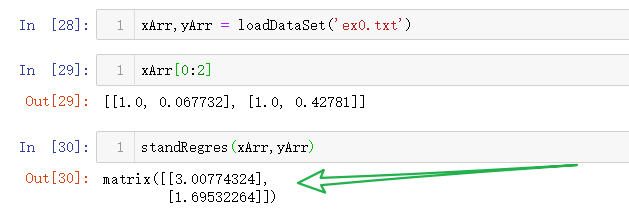
⭐ 则我们的最佳拟合直线为：$y_{Hat} = ws[0]x_0 + ws[1]x_1$
xMat = np.mat(xArr)
yMat = np.mat(yArr)
ws = standRegres(xArr,yArr)
yHat = xMat*ws
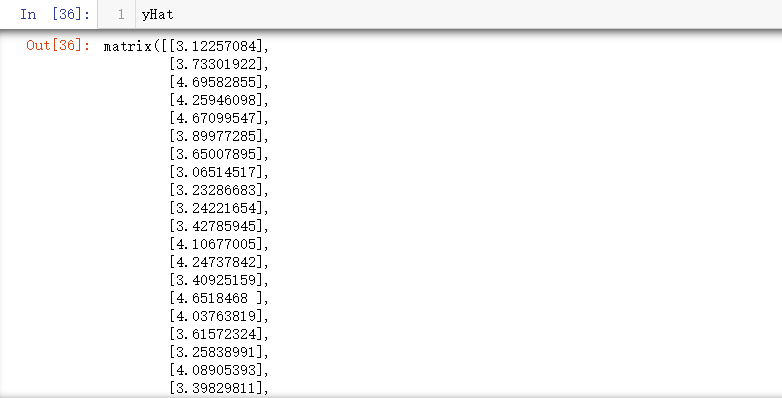
OK，现在就可以绘制最佳直线图：
def regression1():
xArr, yArr = loadDataSet("ex0.txt")
xMat = np.mat(xArr)
yMat = np.mat(yArr)
ws = standRegres(xArr, yArr)
fig = plt.figure()
ax = fig.add_subplot(111) #add_subplot(349)函数的参数的意思是，将画布分成3行4列图像画在从左到右从上到下第9块
ax.scatter(xMat[:, 1].flatten().A[0], yMat.T[:, 0].flatten().A[0]) #scatter 的x是xMat中的第二列，y是yMat的第一列
xCopy = xMat.copy()
xCopy.sort(0)
yHat = xCopy * ws
ax.plot(xCopy[:, 1], yHat)
plt.show()
💡：
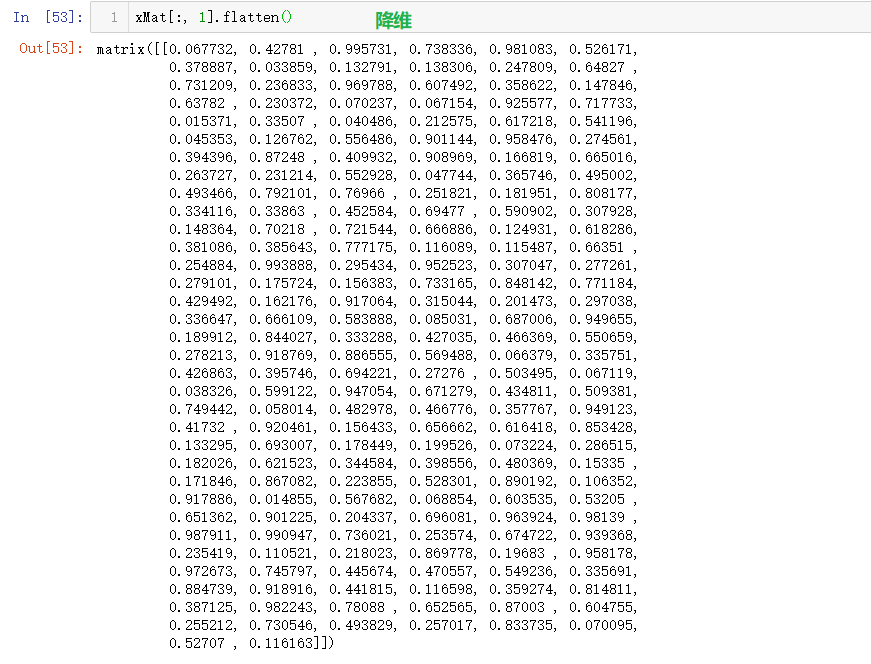
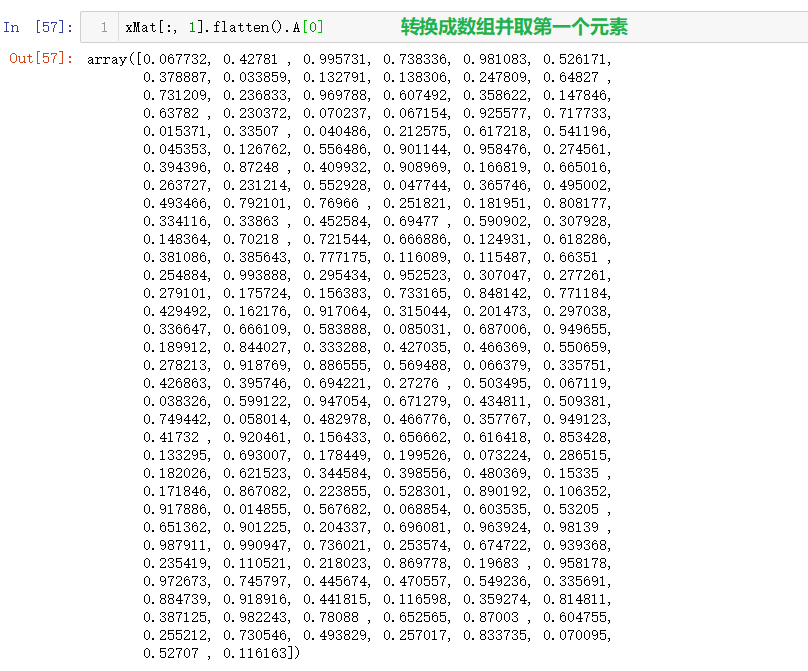
xMat.flatten().A[0]解析：
xMat是个矩阵，xMat.flatten()就是把xMat降到一维，默认是按横的方向降。降维后xMat还是个矩阵，矩阵.A（等效于矩阵.getA()）将矩阵转换成数组，A[0]就是数组里的第一个元素
🏃 代码运行结果如下：
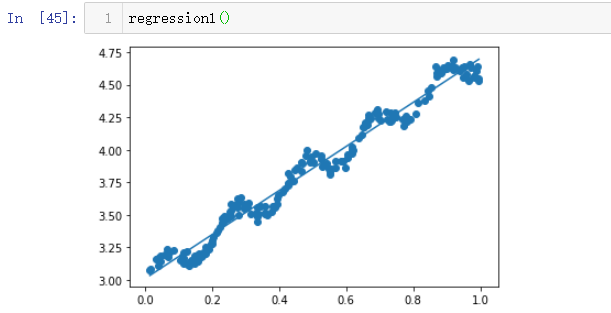
2. 局部加权线性回归 Locally Weighted Linear Regression, LWLR
线性回归的一个问题是有可能出现欠拟合现象，因为它求的是具有最小均方差的无偏估计。显而易见，如果模型欠拟合将不能取得最好的预测效果。所以有些方法允许在估计中引入一些偏差，从而降低预测的均方误差。
其中一个方法是局部加权线性回归（Locally Weighted Linear Regression，LWLR）。⭐ 它的核心思想是：在做预测时，更多地参考距离预测样本近的已知样本，而更少地参考距离预测样本远的已知样本。
在这个算法中，我们给预测点附近的每个点赋予一定的权重，然后与 线性回归 类似，在这个子集上基于最小均方误差来进行普通的回归。
与 kNN 一样，这种算法每次预测均需要事先选出对应的数据子集。⭐ 该算法解出回归系数 w 的形式如下：
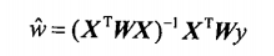
🚨 注意：式中的 W 是权重矩阵，用来给每个数据点赋予权重，而 $\hat w$ 是回归系数。两者不要搞混了！
📜 权重矩阵 W 的求解如下：
LWLR 使用 核 来对附近的点赋予更高的权重。核的类型可以自由选择，最常用的核就是高斯核。$w^{(i)}$ 表示每一个样本的权重：
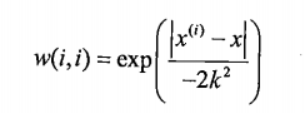
🚩 这样就构建了一个只含对角元素的权重矩阵 W，并且点 x(i)（表示特定的需预测样本） 与 x（表示已知样本 — 数据集中的每个点） 越近，该点 $x^{(i)}$ 的权重 w(i) 将会越大。已知样本与预测样本的距离越远，该已知样本的权重就会越小。
随着已知样本与预测样本距离的增加，权重将以指数级衰减，输入参数 k 控制衰减的速度，这也是使用 LWLR 时唯一需要考虑的参数，下面的图给出了参数 k 与权重的关系：
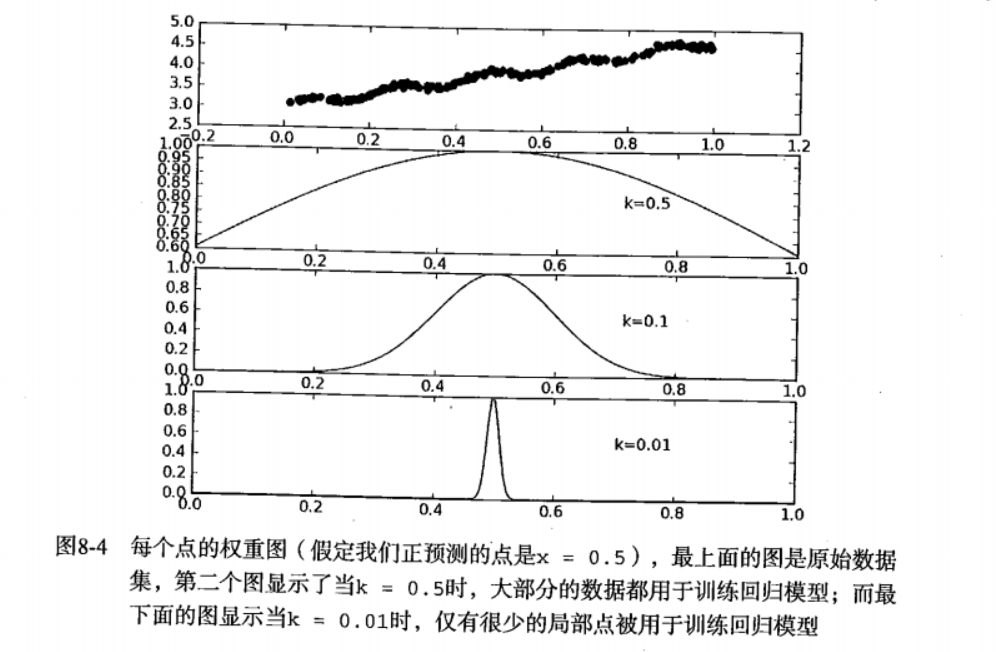
从上图可知，k 越大权重减小的速率越慢，k 越小权重减小的速率越快
💡 我觉得可以这样理解：
k越大表示每个待测点用来训练的数据点越多。k越小表示每个待测点用来训练的数据点越少。
Python 实现局部加权线性回归函数：
def lwlr(testPoint, xArr, yArr, k = 1.0):
"""
Desc:
局部加权线性回归函数,单点估计
Args:
testPoint: 需预测的数据点（待测数据点）
xArr：特征矩阵(用于训练的数据集)
yArr：标签矩阵
k: 手动设置参数 k
"""
xMat = np.mat(xArr)
yMat = np.mat(yArr).T
m = np.shape(xMat)[0] # m 是样本个数
weights = np.mat(np.eye((m))) # 创建一个对角矩阵用来保存权重w
for j in range(m):
diffMat = testPoint - xMat[j,:] # 预测样本 - 已知样本
weights[j,j] = np.exp(diffMat*diffMat.T/(-2.0*k**2))
xTx = xMat.T *(weights * xMat)
if np.linalg.det(xTx) == 0.0:
print("矩阵不可逆！")
return
ws = xTx.I * (xMat.T * weights * yMat) # 回归系数
return testPoint * ws # 返回加权线性回归后的数据点预测值
def lwlrTest(testArr, xArr, yArr, k = 1.0):
"""
Desc:
利用 lwlr 进行预测，数据集所有点的估计
给定特征集，输出预测集 yHat
Args:
testArr: 待测数据集
xArr: 用于训练的数据集
"""
m = np.shape(testArr)[0]
yHat = np.zeros(m)
for i in range(m):
yHat[i] = lwlr(testArr[i], xArr, yArr, k)
return yHat # 返回所有数据点加权线性回归后的预测值
预测某个点的标签值：
预测数据集所有点的标签值：
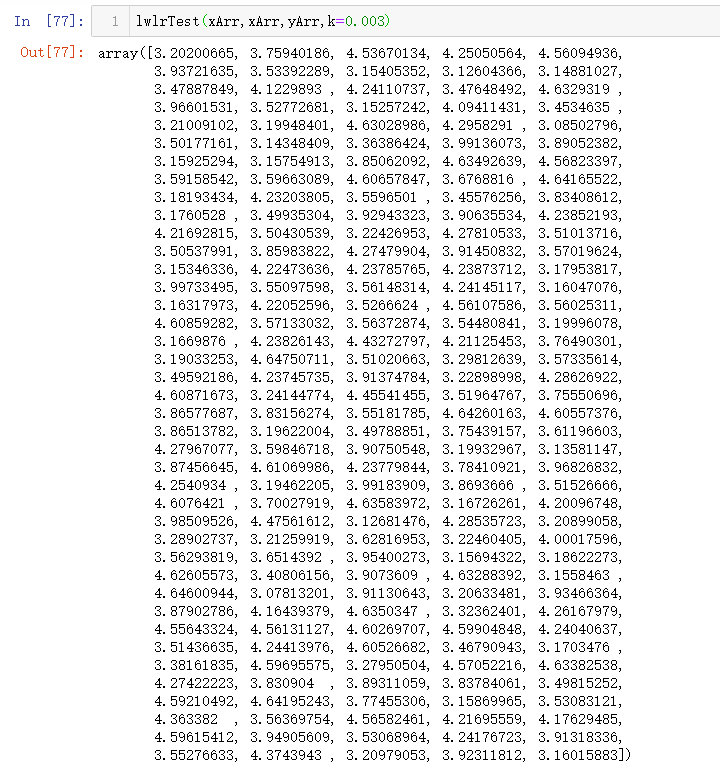
接下来可视化这条最佳拟合直线：
#test for LWLR
def regression2():
xArr, yArr = loadDataSet("ex0.txt")
yHat = lwlrTest(xArr, xArr, yArr, 0.003)
xMat = np.mat(xArr)
srtInd = xMat[:,1].argsort(0) # argsort()函数是将x中的元素从小到大排列，提取其对应的index(索引)，然后输出
xSort=xMat[srtInd][:,0,:] # 排序
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(xSort[:,1], yHat[srtInd]) # 最佳拟合直线
ax.scatter(xMat[:,1].flatten().A[0], np.mat(yArr).T.flatten().A[0] , s=2, c='red') # 原始数据集
plt.show()
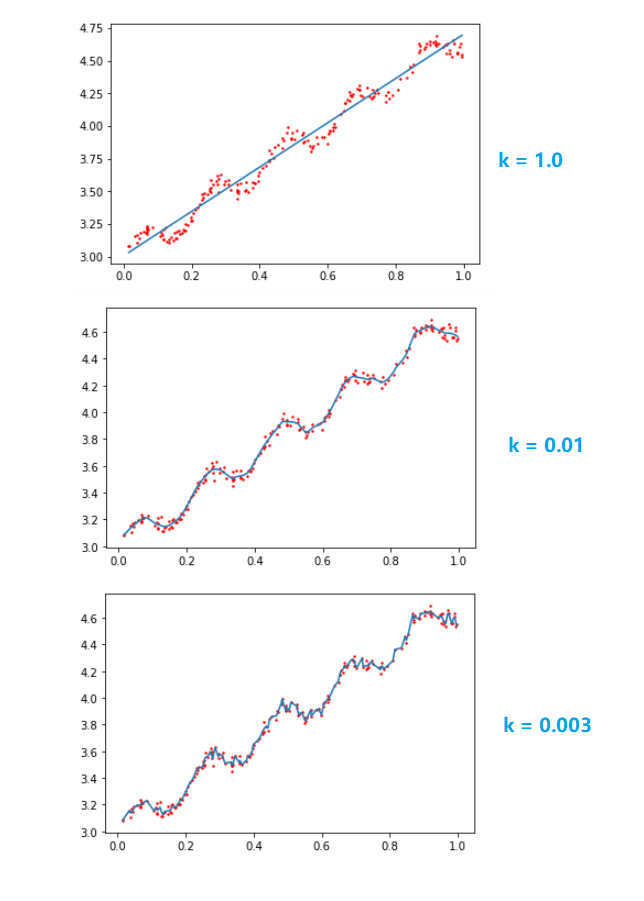
如同可知，当 k = 1.0 时，如同将所有的数据视为等权重，得出的最佳拟合直线和标准的线性回归一致。
当 k = 0.01 时，效果最好
当 k = 0.03 时，发生了过拟合。
3. 示例：预测鲍鱼的年龄
到此为止，我们已经介绍了找出最佳拟合直线的两种方法，下面我们用这些技术来预测鲍鱼的年龄。鲍鱼年龄可以从鲍鱼壳的层数推算得到。
数据集如下：
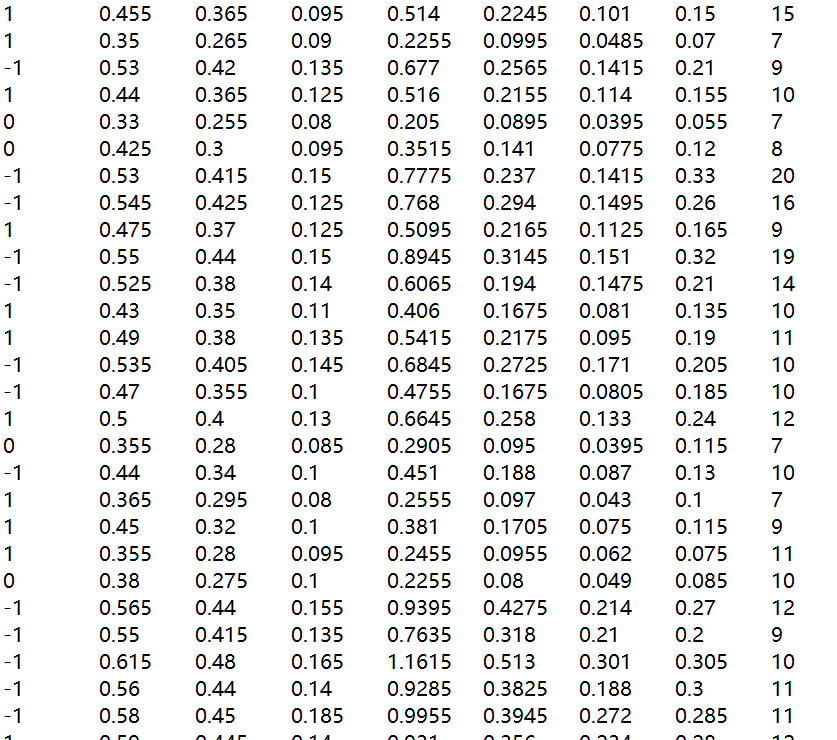
首先，加载数据集，并使用局部加权线性回归算法进行预测，选择不同的参数 k
abX,abY = loadDataSet('abalone.txt')
yHat01 = lwlrTest(abX[0:99], abX[0:99], abY[0:99], 0.1)
yHat1 = lwlrTest(abX[0:99], abX[0:99], abY[0:99], 1)
yHat10 = lwlrTest(abX[0:99], abX[0:99], abY[0:99], 10)
定义代价函数（平方误差函数）：
# 平方误差函数（代价函数）
def rssError(yArr,yHatArr):
"""
Args:
yArr: 实际标签集
yHatArr: 预测标签集
"""
return((yArr - yHatArr)**2).sum()
比较上述预测的误差：
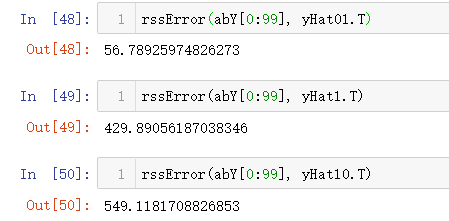
可以看到，使用较小的 k 将得到较小的训练误差。
🚨 注意，我们仅取了 100 个数据进行训练，为什么不在所有数据集上都使用 k = 0.1 呢？因为这样会造成过拟合，对新数据不一定能达到最好的预测效果。
下面我们来看看在测试数据集上的表现：
yHat01 = lwlrTest(abX[100:199], abX[0:99], abY[0:99], 0.1)
yHat1 = lwlrTest(abX[100:199], abX[0:99], abY[0:99], 1)
yHat10 = lwlrTest(abX[100:199], abX[0:99], abY[0:99], 10)
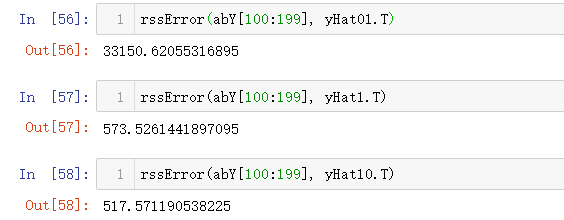
可以看到，使用较大的 k 将得到较小的测试误差。
接下来，再和标准的线性回归做个对比：
根据我们上边的测试，可以看出：标准线性回归达到了与局部加权现行回归类似的效果。这也说明了一点，必须在未知数据上比较效果才能选取到最佳模型。那么最佳的核大小是 10 吗？或许是，但如果想得到更好的效果，可以尝试用 10 个不同的样本集做 10 次测试来比较结果。
4. 缩减系数来理解数据
如果数据的特征比样本点还多应该怎么办？是否还可以使用线性回归和之前的方法来做预测？答案是否定的，即我们不能再使用前面介绍的方法。这是因为在计算 $(XTX)$ 的时候会出错。
如果特征比样本点还多 (n > m)，也就是说输入数据的矩阵 X 不是满秩矩阵。非满秩矩阵求逆时会出现问题。
为了解决这个问题，统计学家引入了 岭回归（ridge regression）这种缩减方法。接着是 lasso法，该方法效果很好但是计算复杂。最后介绍前向逐步回归，可以得到与 lasso 差不多的效果，而且更容易实现。
① 岭回归
简单来说，岭回归就是在矩阵 $(X^TX)$ 上加一个 $λI$ 从而使得矩阵非奇异，进而能对 $(X^TX+λI)$求逆。其中矩阵$I$ 是一个 $n * n$ （等于列数） 的单位矩阵， 对角线上元素全为1，其他元素全为 0。而 $λ$ 是一个用户定义的数值，后面会做介绍。在这种情况下，回归系数的计算公式将变成：
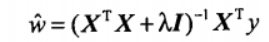
岭回归最先用来处理特征数多于样本数的情况，现在也用于在估计中加入偏差，从而得到更好的估计。这里通过引入 $λ$ 来限制了所有 $w$ 之和，通过引入该惩罚项，能够减少不重要的参数，这个技术在统计学中也叫作 缩减(shrinkage)。
缩减方法可以去掉不重要的参数，因此能更好地理解数据。此外，与简单的线性回归相比，缩减法能取得更好的预测效果。
⚪ 与前面的训练方法一样，首先通过预测误差最小化得到 λ； 数据获取之后，抽一部分数据用于测试，剩余的作为训练集用于训练参数 w。训练完毕后在测试集上测试预测性能。通过选取不同的 λ 来重复上述测试过程，最终得到一个使预测误差最小的 λ 。
def ridgeRegres(xMat, yMat,lam = 0.2):
"""
Desc:
利用岭回归求解回归系数 w
"""
xTx = xMat.T * xMat
denom = xTx + np.eye(np.shape(xMat)[1])*lam # xTx + lambda * I
if np.linalg.det(denom) == 0.0: # 不可逆
print("矩阵不可逆！")
return
ws = denom.I * (xMat.T * yMat)
return ws
def ridgeTest(xArr, yArr):
xMat = np.mat(xArr)
yMat = np.mat(yArr).T
# 数据标准化：（特征 - 均值） / 方差
yMean = np.mean(yMat,0)
yMat = yMat - yMean
xMean = np.mean(xMat,0)
xVar = np.var(xMat, 0) # 方差
xMat = (xMat - xMean) / xVar
numTestPts = 30
wMat = np.zeros((numTestPts, np.shape(xMat)[1]))
for i in range(numTestPts):
ws = ridgeRegres(xMat, yMat, np.exp(i-10)) # 在 30 个不同的 lambda 下运行 ridgeRegres 函数，获取不同的回归系数 w
wMat[i,:] = ws.T
return wMat # 返回回归系数矩阵
下面看一下在鲍鱼数据集上的运行结果：
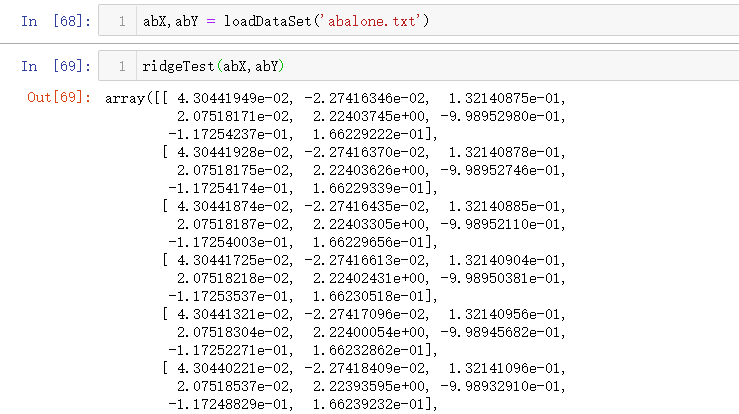
这样就得到了 30 个不同的 λ 所对应的回归系数。为了看到缩减的效果，我们对数据进行可视化：
def regression3():
abX,abY = loadDataSet("abalone.txt")
ridgeWeights = ridgeTest(abX, abY)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(ridgeWeights)
plt.show()
🏃 运行结果如下：
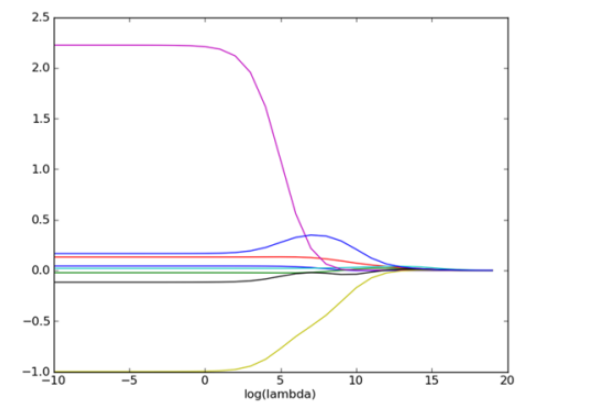
上图绘制出了回归系数与 log(λ) 的关系。在最左边，即 λ 最小时，可以得到所有系数的原始值（与线性回归一致）；而在右边，系数全部缩减为0；在中间部分的某值将可以取得最好的预测效果。为了定量地找到最佳参数值，还需要进行交叉验证。另外，要判断哪些变量对结果预测最具有影响力，在上图中观察它们对应的系数大小就可以了。
还有其他缩减方法，比如 lasso，与岭回归一样，这些方法不仅额可以提高预测精确率，而且可以解释回归系数。👇
② 套索方法 Lasso
Lasso，The Least Absolute Shrinkage and Selection Operator
在增加如下约束时，普通的最小二乘法回归会得到与岭回归一样的公式:
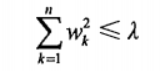
上式限定了所有回归系数的平方和不能大于 λ 。使用普通的最小二乘法回归在当两个或更多的特征相关时，可能会得到一个很大的正系数和一个很大的负系数。正是因为上述限制条件的存在，使用岭回归可以避免这个问题。
与岭回归类似，缩减方法 lasso 也对回归系数做了限定，对应的约束条件如下:
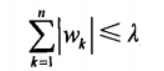
唯一的不同点在于，这个约束条件使用绝对值取代了平方和。虽然约束形式只是稍作变化，结果却大相径庭: 在 λ 足够小的时候，一些系数会因此被迫缩减到 0。这个特性可以帮助我们更好地理解数据。
③ 前向逐步回归
前向逐步回归算法可以得到与 lasso 差不多的效果，但更加简单。它属于一种贪心算法，即每一步都尽可能减少误差。一开始，所有权重都设置为 0，然后每一步所做的决策是对某个权重增加或减少一个很小的值。
📑 伪代码如下:
数据标准化，使其分布满足 0 均值 和单位方差
在每轮迭代过程中:
设置当前最小误差 lowestError 为正无穷
对每个特征:
增大或缩小:
改变一个系数得到一个新的 w
计算新 w 下的误差
如果误差 Error 小于当前最小误差 lowestError: 设置 Wbest 等于当前的 W
将 W 设置为新的 Wbest
📑 Python 实现：
def stageWise(xArr,yArr,eps = 0.01, numIt = 100):
"""
Args:
xArr： 输入数据
yArr： 预测变量
eps：表示每次迭代调整的步长
numIt: 迭代次数
"""
xMat = np.mat(xArr)
yMat = np.mat(yArr).T
# 标准化
yMean = np.mean(yMat,0)
yMat = yMat - yMean
xMean = np.mean(xMat,0)
xVar = np.var(xMat, 0) # 方差
xMat = (xMat - xMean) / xVar
m,n = np.shape(xMat)
returnMat = np.zeros((numIt,n))
ws = np.zeros((n,1))
wsTest = ws.copy()
wsMax =ws.copy()
for i in range(numIt):
print(ws.T)
lowestError = np.inf; # 最小误差
for j in range(n):
# 分别计算增加或减少该特征对误差的影响
for sign in [-1,1]:
wsTest = ws.copy()
wsTest[j] += eps*sign # 更新
yTest = xMat*wsTest
rssE = rssError(yMat.A,yTest.A)
if rssE < lowestError:
lowestError = rssE
wsMax = wsTest
ws = wsMax.copy()
returnMat[i,:] = ws.T
return returnMat # 返回回归系数更新矩阵
🏃 运行该代码：
xArr,yArr=loadDataSet('abalone.txt')
weights = stageWise(xArr,yArr,0.01,200)
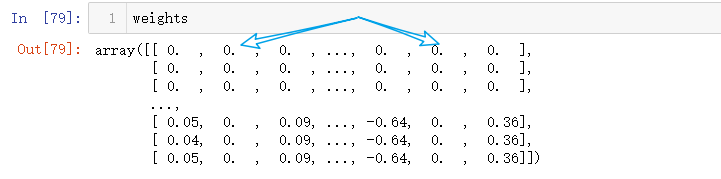
可以看到，$w_1$ 和 $w_6$ 都是 0，这表明它们不对目标值造成任何影响，也就说这些特征很可能是不需要的。
例外，在参数 eps 设置为 0.01 的情况下，一段时间后回归系数已经饱和了，并在特定值之间来回震荡，这是因为步长太大的缘故。这里可以看到，第一个权重 在 0.04 和 0.05 之间来回震荡。
OK，我们减小步长并增多迭代次数：
weights = stageWise(xArr,yArr,0.001,5000)
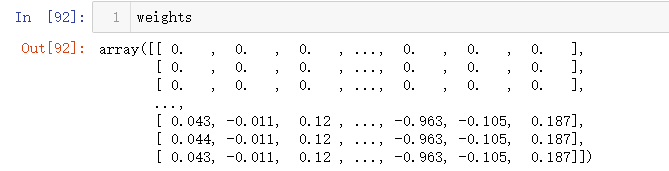
将这些结果和标准线性回归（最小二乘法）进行比较：
xMat = np.mat(xArr)
yMat = np.mat(yArr).T
# 标准化
yMean = np.mean(yMat,0)
yMat = yMat - yMean
xMean = np.mean(xMat,0)
xVar = np.var(xMat, 0) # 方差
xMat = (xMat - xMean) / xVar
weights = standRegres(xMat,yMat.T)
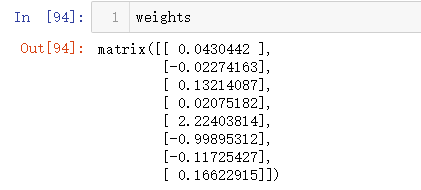
可以看到，在 5000 次迭代之后，前向逐步回归算法与标准的线性回归（最小二乘法）效果类似。
🎁 逐步线性回归算法的主要优点在于它可以帮助人们理解现有的模型并作出改进。当构建了一个模型后，可以运行前向逐步回归算法找出重要的特征，这样就有可能及时停止对那些不重要特征的收集。最后，如果用于测试，该算法每 100次 迭代后就可以构建出一个模型，可以使用类似于10 折交叉验证的方法比较这些模型，最终选择使误差最小的模型。
5. 权衡偏差与方差
当应用缩减方法（如逐步线性回归或岭回归）时，模型也就增加了偏差（bias），与此同时却减小了模型的方差。
任何时候，一旦发现模型和测量值之间存在差异，就说出现了误差。当考虑模型中的 “噪声” 或者说误差时，必须考虑其来源。你可能会对复杂的过程进行简化，这将导致在模型和测量值之间出现 “噪声” 或误差，若无法理解数据的真实生成过程，也会导致差异的产生。另外，测量过程本身也可能产生 “噪声” 或者问题。
下面我们举一个例子，比如说我们利用下列公式生成一个数据集：
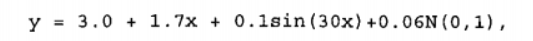
其中的 N(0, 1) 是一个均值为 0、方差为 1 的正态分布。显然，如果我们尝试用直线来拟合该数据集，那么能得到的最佳拟合仅仅是 $y = 3.0 + 1.7x$ 这部分，剩余部分便是误差部分。
下图给出了训练误差和测试误差的曲线图，上面的曲线就是测试误差，下面的曲线是训练误差。我们根据 预测鲍鱼年龄 的实验知道: 如果降低参数 k （核）的大小，那么训练误差将变小。从下图开看，从左到右就表示了参数 k 逐渐减小的过程。
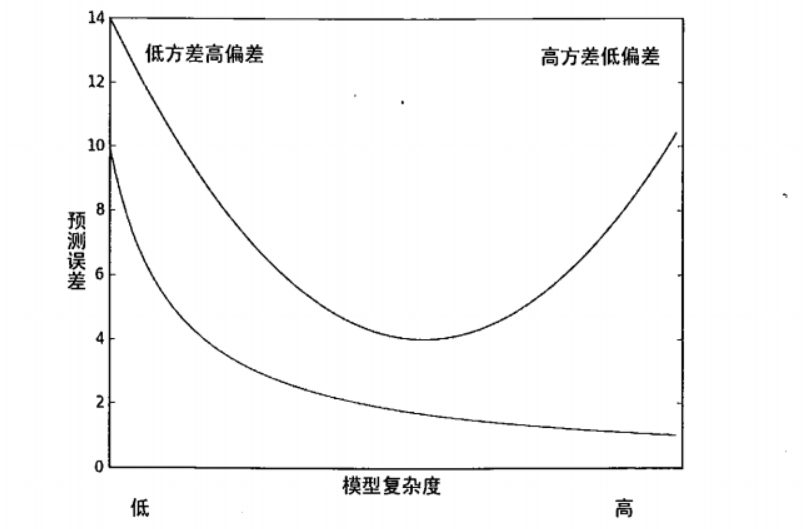
⭐ 总结来说：
- 模型复杂度越低，即方差越低 + 偏差越高
- 模型复杂度越高，即方差越高 + 偏差越低
✅ End
有时候预测值与特征之间是非线性关系，就无法利用线性模型拟合数据集，那么本章介绍的方法就很难适用。下一章将介绍几种使用树结构来预测数据的方法。
📚 References
-
《Machine Learning in Action》
-
《统计学习方法 - 李航》
-
《机器学习 - 周志华》
