4
💯 100 numpy exercises
🔊 题目来自黄海广博士整理的 Github - numpy - 100,未翻译的题目就是平常基本很少用到的。
1. 导入 numpy 包并命名 np (★☆☆)
import numpy as np
2. 打印 numpy 的版本和配置信息 (★☆☆)
print(np.__version__) # 1.16.4
np.show_config()
3. 创建一个大小为 10 的一维空数组 (★☆☆)
Z = np.zeros(10)
print(Z) # array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
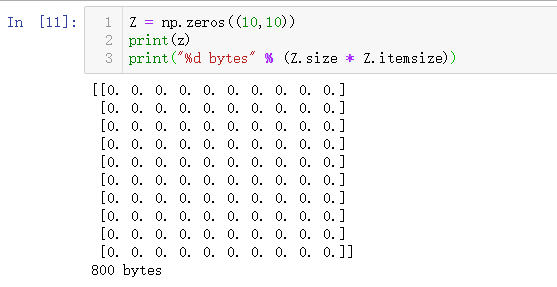
4. 查询任意数组的内存大小(★☆☆)
Z = np.zeros((10,10)) # 创建一个 10 x 10 的二维数组
print("%d bytes" % (Z.size * Z.itemsize)) # 800bytes
💡 NumPy 的数组中比较重要的 ndarray 对象属性有:
属性 说明 ndarray.ndim 秩,即轴的数量或维度的数量 ndarray.shape 数组的维度,对于数组,n 行 m 列 ndarray.size 数组元素的总个数,相当于 .shape 中 n*m 的值 ndarray.dtype ndarray 对象的元素类型 ndarray.itemsize ndarray 对象中每个元素的大小,以字节为单位 ndarray.flags ndarray 对象的内存信息 ndarray.real ndarray元素的实部 ndarray.imag ndarray 元素的虚部 ndarray.data 包含实际数组元素的缓冲区,由于一般通过数组的索引获取元素,所以通常不需要使用这个属性。
5. 从命令行获取numpy add函数的文档 (★☆☆)
%run `python -c "import numpy; numpy.info(numpy.add)"`
6. 创建一个大小为 10 的一维空数组,但是第 5 个元素值为 1(★☆☆)
Z = np.zeros(10)
Z[4] = 1
print(Z) # array([0., 0., 0., 0., 1., 0., 0., 0., 0., 0.])
7. 创建一个数值从 10 到 49 的一维数组(★☆☆)
Z = np.arange(10,50)
print(Z) # array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49])
8. 翻转数组 (★☆☆)
Z = np.arange(10,50)
Z = Z[::-1]
print(Z) # array([49, 48, 47, 46, 45, 44, 43, 42, 41, 40, 39, 38, 37, 36, 35, 34, 33, 32, 31, 30, 29, 28, 27, 26, 25, 24, 23, 22, 21, 20, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10])
9. 以数值 0 到 8 创建一个 3x3 的数组 (★☆☆)
Z = np.arange(9).reshape(3, 3)
print(Z)
# array([[0, 1, 2],
# [3, 4, 5],
# [6, 7, 8]])
💡
reshape()是数组对象中的方法,用于改变数组的形状。a = np.array([1,2,3,4,5,6,7,8]) # 一维数组 d = a.reshape((2,4)) # 改为一个 2x4 的二维数组 e = a.reshape((2,2,2)) # 改为一个 2x2x2 的三维数组
10. 从一维数组 [1,2,0,0,4,0] 中查询非 0 元素的下标(★☆☆)
nz = np.nonzero([1,2,0,0,4,0])
print(nz) # (array([0, 1, 4], dtype=int64),)
💡
Numpy.nonzero()返回的是数组中非零元素的位置
11. 创建一个 3x3 的单位数组 (★☆☆)
Z = np.eye(3)
print(Z)
# array([[1., 0., 0.],
# [0., 1., 0.],
# [0., 0., 1.]])
💡 函数
eye()的作用是返回一个对角线上全是1,而其他位置全为0的一个二维数组(2D-array)。numpy.eye(N,M =无,k = 0,dtype = <class’flove’>,order =‘C’ )参数:
N : int
输出中的行数。
M : int,可选
输出中的列数。如果无,默认为Ñ。
k : int,可选
对角线的索引:0(默认值)指的是主对角线,正值指的是上对角线,负值指的是下对角线。
dtype : 数据类型,可选
返回数组的数据类型。
order: {‘C’,‘F’},可选
输出是否应以内存中的行主(C风格)或列主(Fortran风格)顺序存储。
12. 以随机数创建一个 3x3x3 的三维数组 (★☆☆)
Z = np.random.random((3,3,3))
print(Z)
# array([[[0.36542095, 0.34831083, 0.17366236],
# [0.06457177, 0.05966199, 0.68338232],
# [0.1559074 , 0.67245645, 0.92502575]],
#
# [[0.87001758, 0.70293207, 0.4071415 ],
# [0.83547065, 0.47895394, 0.14842163],
# [0.48194952, 0.71887822, 0.75624038]],
#
# [[0.18812376, 0.72727565, 0.72370348],
# [0.98153472, 0.63258681, 0.68735608],
# [0.62900498, 0.58925055, 0.39368417]]])
13. 以随机数创建一个 10x10 的二维数组,并查询最大值和最小值 (★☆☆)
Z = np.random.random((10,10))
Zmin, Zmax = Z.min(), Z.max()
print(Zmin, Zmax) # 0.00898087017034821 0.9952435535747781
14. 以随机数创建一个大小为 30 的一维数组,并查询平均值 (★☆☆)
Z = np.random.random(30)
m = Z.mean()
print(m)
15. 创建一个外围边界全是 1、内部全是 1 的二维数组 (★☆☆)
Z = np.ones((10,10))
print(Z)
# array([[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]])
Z[1:-1,1:-1] = 0
print(Z)
# array([[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
# [1., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
# [1., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
# [1., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
# [1., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
# [1., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
# [1., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
# [1., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
# [1., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
# [1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]])
16. 给一个已经存在的二维数组周围添加全 0 边界 (★☆☆)
Z = np.ones((5,5))
print(Z)
# array([[1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1.]])
Z = np.pad(Z, pad_width=1, mode='constant', constant_values=0)
print(Z)
# array([[0., 0., 0., 0., 0., 0., 0.],
# [0., 1., 1., 1., 1., 1., 0.],
# [0., 1., 1., 1., 1., 1., 0.],
# [0., 1., 1., 1., 1., 1., 0.],
# [0., 1., 1., 1., 1., 1., 0.],
# [0., 1., 1., 1., 1., 1., 0.],
# [0., 0., 0., 0., 0., 0., 0.]])
# 使用花式索引
Z[:, [0, -1]] = 0
Z[[0, -1], :] = 0
print(Z)
💡 函数
eye()解析:ndarray = numpy.pad(array, pad_width, mode, **kwargs)
array 为要填补的数组
pad_width 是在各维度的各个方向上想要填补的长度
如((1,2),(2,2)),表示在第一个维度上水平方向上 padding = 1, 垂直方向上 padding=2, 在第二个维度上水平方向上padding=2, 垂直方向上padding=2。
如果直接输入一个整数,则说明各个维度和各个方向所填补的长度都一样。
mode 为填补类型,即怎样去填补,有“constant”,“edge”等模式,如果为constant模式,就得指定填补的值,如果不指定,则默认填充 0。
剩下的都是一些可选参数,具体可查看
[https://docs.scipy.org/doc/numpy/reference/generated/numpy.pad.html](https://www.cnblogs.com/hezhiyao/p/ https://docs.scipy.org/doc/numpy/reference/generated/numpy.pad.html)ndarray 为填充好的返回值
17. 以下表达式的结果是什么? (★☆☆)
print(0 * np.nan) # nan
print(np.nan == np.nan) # False 两个nan是不相等的
print(np.inf > np.nan) # False
print(np.nan - np.nan) # nan
print(np.nan in set([np.nan])) # True
print(0.3 == 3 * 0.1) # False
💡 Numpy 之 nan 和 Inf 处理:
Nan:Not a number
Inf:Infinity(无穷大)
-Inf:Infinity(负无穷大)
当然容易搞混的还有 None,None 是 python 中用于标识空缺数据,Nan是nunpy和pandas中用于标识空缺数据,None 是一个 python 特殊的数据类型, 但是 Nan 和 Inf 的数据类型都是 float
18. 创建一个 5x5 数组,数值 1,2,3,4 在对角线正下方 (★☆☆)
Z = np.diag(1+np.arange(4),k=-1)
print(Z)
# [[0 0 0 0 0]
# [1 0 0 0 0]
# [0 2 0 0 0]
# [0 0 3 0 0]
# [0 0 0 4 0]]
💡
numpy.diag(v,k=0):
参数 v : 如果 v 是 2D 数组,返回 k 位置的对角线。
如果 v 是 1D 数组,返回一个 v 作为 k 位置对角线的 2 维数组。
参数 k : 对角线的位置,大于零位于对角线上面,小于零则在下面。
k = -1 表示在对角线的下面一行
k = -2 表示在对角线的下面两行
k = 1 表示在对角线的上面一行
19. 创建一个 8x8 数组,并用棋盘图案填充 (★☆☆)
Z = np.zeros((8,8),dtype=int)
Z[1::2,::2] = 1 # 从第1行开始,每隔2行进行切片;从第0列开始,每隔2列进行切片
# [[0 0 0 0 0 0 0 0]
# [1 0 1 0 1 0 1 0]
# [0 0 0 0 0 0 0 0]
# [1 0 1 0 1 0 1 0]
# [0 0 0 0 0 0 0 0]
# [1 0 1 0 1 0 1 0]
# [0 0 0 0 0 0 0 0]
# [1 0 1 0 1 0 1 0]]
Z[::2,1::2] = 1
print(Z)
# [[0 1 0 1 0 1 0 1]
# [1 0 1 0 1 0 1 0]
# [0 1 0 1 0 1 0 1]
# [1 0 1 0 1 0 1 0]
# [0 1 0 1 0 1 0 1]
# [1 0 1 0 1 0 1 0]
# [0 1 0 1 0 1 0 1]
# [1 0 1 0 1 0 1 0]]
20. 对于一个 shape = (6,7,8) 的数组,第100个元素的下标是多少?
shape = (6,7,8) 表示数组维度 6 x 7 x 8
print(np.unravel_index(99,(6,7,8))) # (1, 5, 3)
💡
numpy.unravel_index()函数的作用是获取一个int类型的索引值在多维数组中的位置。
21. 使用 tile 函数创建一个棋盘图案的 8x8 数组 (★☆☆)
Z = np.tile( np.array([[0,1],[1,0]]), (4,4))
print(Z)
💡 Numpy的
tile()函数,就是将原数组横向、纵向地复制。tile 是瓷砖的意思,顾名思义,这个函数就是把数组像瓷砖一样铺展开来。举个例子,原数组:
mat = array([[1,2], [3, 4]])横向:
tile(mat, (1, 4)) # 等同于 tile(mat, 4)
[[1 2 1 2 1 2 1 2] [3 4 3 4 3 4 3 4]]纵向:
tile(mat, (3, 1))
结果:
[[1 2] [3 4] [1 2] [3 4] [1 2] [3 4]]横向 + 纵向:
tile(mat, (3, 4))
结果:
[[1 2 1 2 1 2 1 2] [3 4 3 4 3 4 3 4] [1 2 1 2 1 2 1 2] [3 4 3 4 3 4 3 4] [1 2 1 2 1 2 1 2] [3 4 3 4 3 4 3 4]]
22. 归一化 5x5 随机数组 (★☆☆)
💡 数组归一化,说白了就是整体乘一个系数,使数组的绝对值 = 1
Z = np.random.random((5,5))
Z = (Z - np.mean (Z)) / (np.std (Z))
print(Z)
23. 自定义一个类型,用 4 个无符号字节来表示 RGBA (★☆☆)
color = np.dtype([("r", np.ubyte, 1),
("g", np.ubyte, 1),
("b", np.ubyte, 1),
("a", np.ubyte, 1)])
24. 5x3 的实数数组和 3x2 的实数数组相乘 (★☆☆)
Z = np.dot(np.ones((5,3)), np.ones((3,2)))
print(Z)
# [[3. 3.]
# [3. 3.]
# [3. 3.]
# [3. 3.]
# [3. 3.]]
# Alternative solution, in Python 3.5 and above
Z = np.ones((5,3)) @ np.ones((3,2))
print(Z)
25. 把一维数组中值在 3 ~ 8 之间的元素取反 (★☆☆)
Z = np.arange(11)
Z[(3 < Z) & (Z <= 8)] *= -1
print(Z)
26. 下面表达式的输出是什么? (★☆☆)
print(sum(range(5),-1)) # 9 sum 是python内建函数,sum(sequence[,start]),相当于 -1+1+2+3+4=9
from numpy import *
print(sum(range(5),-1)) # numpy.sum(a, axis=None) ,axis表示沿着哪个轴求和,因为数组是一维的,所以axis的大小没有影响
27. Consider an integer vector Z, which of these expressions are legal? (★☆☆)
Z**Z
2 << Z >> 2
Z <- Z
1j*Z
Z/1/1
Z<Z>Z
28. 下面表达式的输出是什么? (★☆☆)
print(np.array(0) / np.array(0)) # nan
print(np.array(0) // np.array(0)) # 0
print(np.array([np.nan]).astype(int).astype(float)) # [-2.14748365e+09]
29. 如何从零位对浮点数组做四舍五入 ? (★☆☆)
Z = np.random.uniform(-10,+10,10) # 从一个均匀分布[low,high)中随机采样,左闭右开,即包含low,不包含high.
print(Z)
# array([-3.55809668, 7.52396621, 1.83374403, 8.13811486, 6.66503506,
# 7.92331703, 9.62947517, -2.81268468, 4.54531352, 3.43059021])
print(np.copysign(np.ceil(np.abs(Z)), Z)) # 先取绝对值,再取标量的上界,最后赋予之前同样的正负号
# array([-4., 8., 2., 9., 7., 8., 10., -3., 5., 4.])
# More readable but less efficient
print(np.where(Z>0, np.ceil(Z), np.floor(Z)))
30. 查询两个数组中相同的元素 (★☆☆)
Z1 = np.random.randint(0,10,10)
Z2 = np.random.randint(0,10,10)
print(np.intersect1d(Z1,Z2))
💡
numpy.intersect1d(ar1, ar2, assume_unique=False, return_indices=False):返回两个数组中共同的元素
31. 如何忽略所有的 numpy 警告(尽管不建议这么做)? (★☆☆)
# 1. Suicide mode on
defaults = np.seterr(all="ignore")
Z = np.ones(1) / 0
# 2. Back to sanity
_ = np.seterr(**defaults)
# 3. Equivalently with a context manager
with np.errstate(all="ignore"):
np.arange(3) / 0
💡 如果没有忽略警告,
np.arange(3) / 0会发出下列警告:
32. 判断下列表达式是否正确 (★☆☆)
np.sqrt(-1) == np.emath.sqrt(-1)
报错:

💡 具有自动域的数学函数(
numpy.emath / numpy.lib.scimath)注意
numpy.emath是numpy.lib.scimath的首选别名, 在导入numpy后可用。
包装器函数对某些数学函数的调用更加用户友好,这些数学函数的输出数据类型与输入的某些域中的输入数据类型不同。例如:
np.sqrt(-1)这句代码的输出是
nan,因为在实数域里不能对一个负数开平方。np.emath.sqrt(-1)这句代码的输出是
1j,也就是一个虚数(python里虚数不能直接写j,前面必须要加一个常数),这样是不是就理解了前面说的“数学函数的输出数据类型与输入的某些域中的输入数据类型不同”,从实数域可以变到复数域。这句代码的输出是1j,也就是一个虚数(python里虚数不能直接写j,前面必须要加一个常数),这样是不是就理解了前面说的“数学函数的输出数据类型与输入的某些域中的输入数据类型不同”,从实数域可以变到复数域。
————————————————
版权声明:本文为CSDN博主「Econe-wei」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/econe_wei/article/details/103189374
33. 如何得到昨天,今天,明天的日期? (★☆☆)
yesterday = np.datetime64('today') - np.timedelta64(1)
today = np.datetime64('today')
tomorrow = np.datetime64('today') + np.timedelta64(1)
💡 在NumPy 1.7版本开始,它的核心数组(ndarray)对象支持datetime相关功能,由于’datetime’这个数据类型名称已经在Python自带的datetime模块中使用了, NumPy中时间数据的类型称为’datetime64’。
单个时间格式字符串转换为numpy的datetime对象,可使用datetime64实例化一个对象,如下所示:
# 时间字符串转 numpy.datetime64 datetime_nd=np.datetime64('2019-01-01')也可以通过
numpy.arange()函数(见34题),给定时间起始范围去创建numpy的datetime对象数组(array),指定 dtype 为’datetime64’时默认以日为时间间隔,如下所示:datetime_array = np.arange('2019-01-05','2019-01-10', dtype='datetime64') print(datetime_array) # ['2019-01-05' '2019-01-06' '2019-01-07' '2019-01-08' '2019-01-09']设定numpy.arange()函数中的dtype参数,可以调整时间的间隔,比如以年、月、周,甚至小时、分钟、毫秒程度的间隔生成时间数组,这点和Python的datetime模块是一样的,分为了date单位和time单位。如下所示:
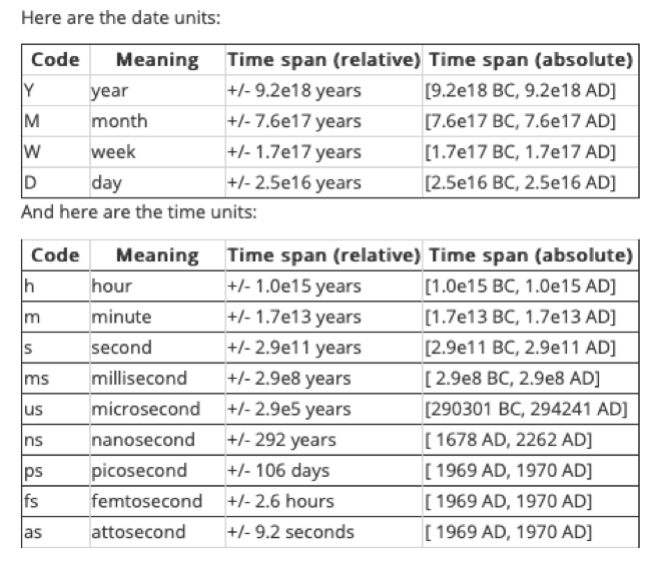
另外,numpy也提供了
datetime.timedelta类的功能,支持两个时间对象的运算,得到一个时间单位形式的数值。因为numpy的核心数组(ndarray)对象没有物理量系统(physical quantities system),所以创建了timedelta64数据类型来补充datetime64。datetime和timedelta结合提供了更简单的datetime计算方法。如下所示:datetime_delta = np.datetime64('2009') + np.timedelta64(20, 'D') # 加20天 print(datetime_delta) # 2009-01-21
34. 如何得到所有 2016 年 7 月的日期? (★★☆)
Z = np.arange('2016-07', '2016-08', dtype='datetime64[D]')
print(Z)
# ['2016-07-01' '2016-07-02' '2016-07-03' '2016-07-04' '2016-07-05'
# '2016-07-06' '2016-07-07' '2016-07-08' '2016-07-09' '2016-07-10'
# '2016-07-11' '2016-07-12' '2016-07-13' '2016-07-14' '2016-07-15'
# '2016-07-16' '2016-07-17' '2016-07-18' '2016-07-19' '2016-07-20'
# '2016-07-21' '2016-07-22' '2016-07-23' '2016-07-24' '2016-07-25'
# '2016-07-26' '2016-07-27' '2016-07-28' '2016-07-29' '2016-07-30'
# '2016-07-31']
35. 就地计算(A+B)*(-A/2) (不建立副本) (★★☆)
A = np.ones(3)*1
B = np.ones(3)*2
C = np.ones(3)*3
np.add(A,B,out=B)
np.divide(A,2,out=A)
np.negative(A,out=A)
np.multiply(A,B,out=A)
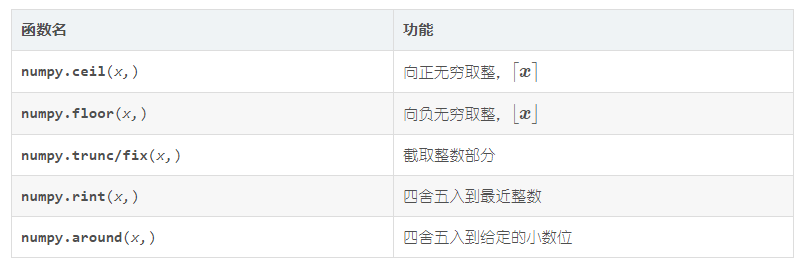
36. 用五种不同的方法去提取一个随机数组的整数部分 (★★☆)
Z = np.random.uniform(0,10,10)
print(Z)
# array([8.92247374, 8.70716226, 2.9064209 , 9.30812563, 8.4894982 ,
# 7.86541565, 3.15193366, 7.83739923, 3.44837548, 1.91167331])
print(Z - Z%1)
print(Z // 1)
print(np.floor(Z)) # 取下整
print(Z.astype(int))
print(np.trunc(Z))
💡 Numpy 数组的取整函数:
37. 创建一个5x5的数组,其中每行的数值范围从 0 到 4 (★★☆)
Z = np.zeros((5,5))
Z += np.arange(5)
print(Z)
# array([[0., 1., 2., 3., 4.],
# [0., 1., 2., 3., 4.],
# [0., 1., 2., 3., 4.],
# [0., 1., 2., 3., 4.],
# [0., 1., 2., 3., 4.]])
38. 通过一个自定义的可生成10个整数的函数,来构建一个数组 (★☆☆)
def generate():
for x in range(10):
yield x
Z = np.fromiter(generate(),dtype=float)
print(Z)
💡
numpy.fromiter:该函数从可迭代对象中建立ndarray对象,返回一维数组。
numpy.fromiter(iterable, dtype, count=-1)list=range(5) it=iter(list) x=np.fromiter(it, dtype=float) print(x) # [0. 1. 2. 3. 4.]
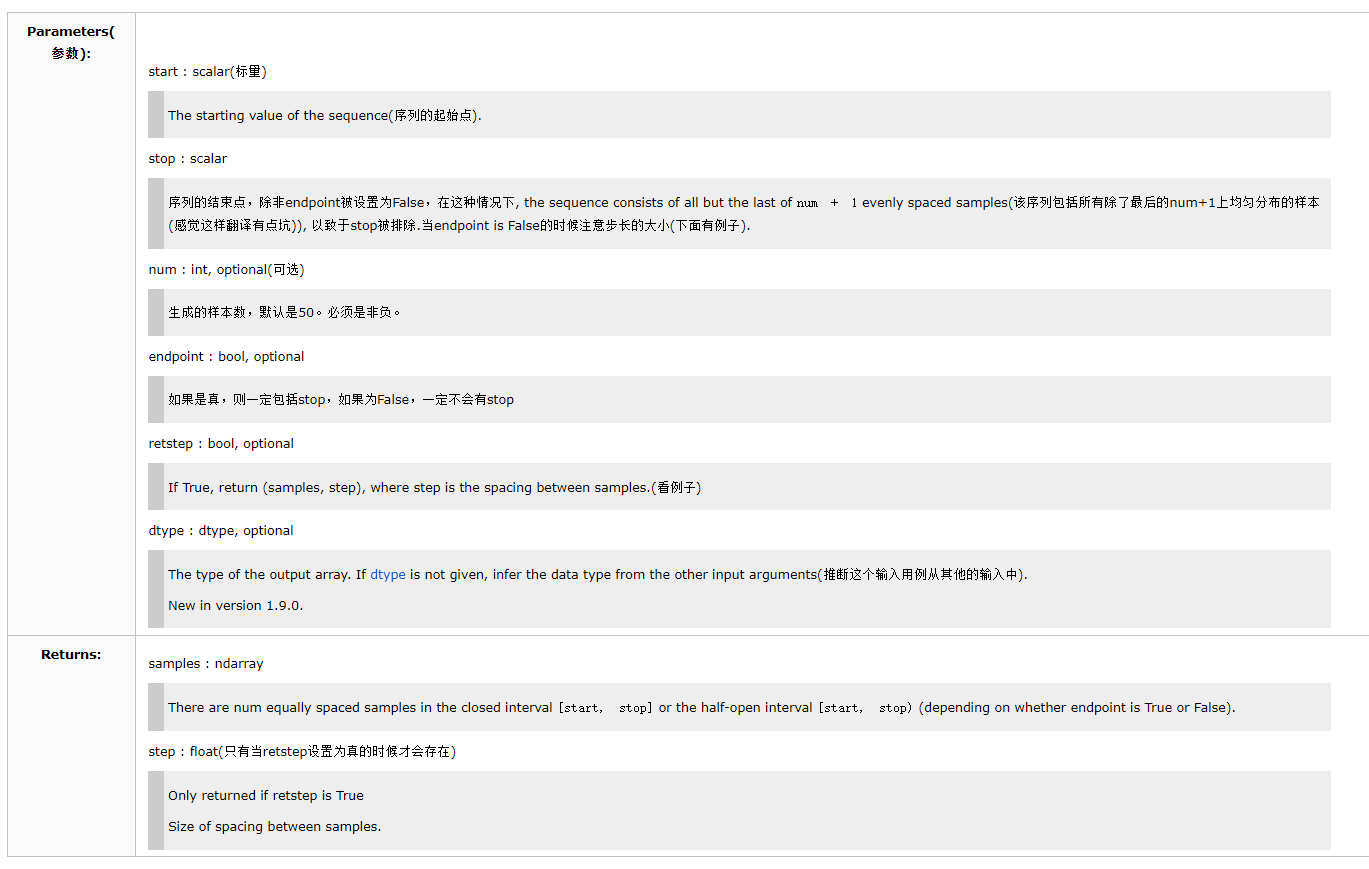
39. 创建一个长度为 10 的随机数组,其值域范围从 0 到 1,但是不包括 0 和 1 (★★☆)
Z = np.linspace(0,1,11,endpoint=False)[1:] # 利用切片去除 0
print(Z) # [0.09090909 0.18181818 0.27272727 0.36363636 0.45454545 0.54545455 0.63636364 0.72727273 0.81818182 0.90909091]
💡
numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)在指定的间隔内返回均匀间隔的数字。返回 num 均匀分布的样本,在 [start, stop]。其中,区间的结束端点可以被排除在外。
40. 创建一个长度为10的随机向量,并将其排序 (★★☆)
Z = np.random.random(10)
Z.sort()
print(Z) # [0.02555939 0.04259598 0.09266813 0.21747377 0.36567196 0.37959098 0.61627334 0.62864999 0.77093929 0.87897974]
💡
random.random()用于生成一个 0 到 1 的随机符点数: 0 <= n < 1.0np.random.random((100, 50))上方代表生成 100 行 50 列的随机浮点数,浮点数范围 : (0 , 1)
值得注意的是
np.random.random([100, 50])效果一样
numpy.random.randn(d0,d1,…,dn)
- randn 函数返回一个或一组样本,具有标准正态分布。
- dn 表格每个维度
- 返回值为指定维度的array
np.random.randn() # 当没有参数时,返回单个数据 # -1.1241580894939212 np.random.randn(2,4) # array([[ 0.27795239, -2.57882503, 0.3817649 , 1.42367345], # [-1.16724625, -0.22408299, 0.63006614, -0.41714538]]) np.random.randn(4,3,2) # array([[[ 1.27820764, 0.92479163], # [-0.15151257, 1.3428253 ], # [-1.30948998, 0.15493686]], # # [[-1.49645411, -0.27724089], # [ 0.71590275, 0.81377671], # [-0.71833341, 1.61637676]], # # [[ 0.52486563, -1.7345101 ], # [ 1.24456943, -0.10902915], # [ 1.27292735, -0.00926068]], # # [[ 0.88303 , 0.46116413], # [ 0.13305507, 2.44968809], # [-0.73132153, -0.88586716]]])标准正态分布介绍
- 标准正态分布 — standard normal distribution
- 标准正态分布又称为u分布,是以0为均值、以1为标准差的正态分布,记为N(0,1)。
41. 如何比 np.sum 更快地求和一个小数组? (★★☆)
Z = np.arange(10)
np.add.reduce(Z)
💡 两者的性能似乎完全不同:对于相对较小的阵列大小,
add.reduce大约比np.sum快两倍。
42. 检查两个随机数组 A 和 B 是否相等 (★★☆)
A = np.random.randint(0,2,5)
B = np.random.randint(0,2,5)
# 如果数组的形状相同,并且允许值有一定的误差,可以使用 allclose 判断是否近似
equal = np.allclose(A,B)
print(equal)
# 准确判断
equal = np.array_equal(A,B)
print(equal)
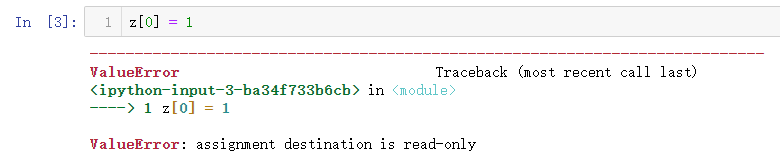
43. 创建一个只读数组 (★★☆)
Z = np.zeros(10)
Z.flags.writeable = False
44. Consider a random 10x2 matrix representing cartesian coordinates, convert them to polar coordinates (★★☆)
Z = np.random.random((10,2))
X,Y = Z[:,0], Z[:,1]
R = np.sqrt(X**2+Y**2)
T = np.arctan2(Y,X)
print(R)
print(T)
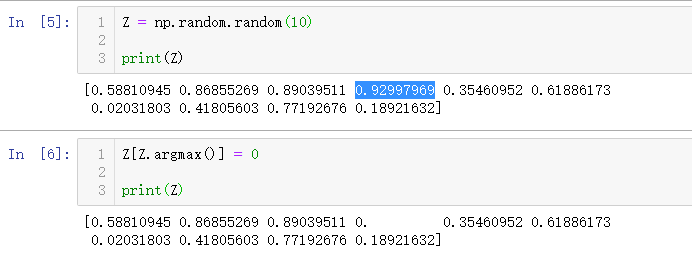
45. 创建大小为 10 的随机数组,并将最大值替换为0 (★★☆)
Z = np.random.random(10)
Z[Z.argmax()] = 0
46. 创建具有 x 和 y 坐标并覆盖 [0,1] X [0,1] 区域的结构化数组 (★★☆)
Z = np.zeros((5,5), [('x',float),('y',float)])
Z['x'], Z['y'] = np.meshgrid(np.linspace(0,1,5),
np.linspace(0,1,5))
print(Z)

💡
zeros(shape, dtype=float, order='C'):
shape: 形状
dtype: 数据类型,可选参数,默认numpy.float64
order: 可选参数,c代表与 c 语言类似,行优先;F代表列优先
💡
meshgrid()生成网格点坐标数组:
A,B,C,D,E,F是6个网格点,坐标如图,如何用数组形式(坐标数组)来批量描述这些点的坐标呢?
答案如下:
这就是坐标数组——横坐标数组 X 中的每个元素,与纵坐标数组 Y 中对应位置元素,共同构成一个点的完整坐标。如 B 点坐标$(X_{12},Y_{12})=(1,1)$
下面可以自己用
matplotlib来试一试,输出就是上边的图import numpy as np import matplotlib.pyplot as plt x = np.array([[0, 1, 2], [0, 1, 2]]) y = np.array([[0, 0, 0], [1, 1, 1]]) plt.plot(x, y, color='red', # 全部点设置为红色 marker='.', # 点的形状为圆点 linestyle='') # 线型为空,也即点与点之间不用线连接 plt.grid(True) plt.show()到这里,网格点和坐标数组的概念就解释清楚了。
那么问题来了,如果需要的图比较大,需要大量的网格点该怎么办呢?比如下面的这种
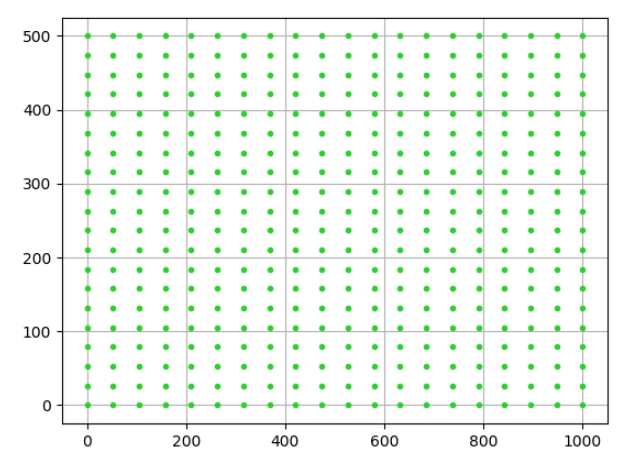
最直接但是最笨的方法,就是按照上面的方法把横纵坐标数组 X,Y写出来,就像上面练习题中的
很明显,对于网格点很多的情况根本没法用。
🚩 注意到我们练习题中的坐标数组,其实有大量的重复—— X 的每一行都一样,Y 的每一列都一样。基于这种强烈的规律性,
numpy提供的numpy.meshgrid()函数可以让我们快速生成坐标数组 X,Y。
语法:X,Y = numpy.meshgrid(x, y)输入的 x,y,就是网格点的横纵坐标列数组(非数组)
输出的 X,Y,就是坐标数组。
我们来试验一下:改写第一个例子中的代码,用
numpy.meshgrid来实现。import numpy as np import matplotlib.pyplot as plt x = np.array([0, 1, 2]) y = np.array([0, 1]) X, Y = np.meshgrid(x, y) print(X) print(Y) plt.plot(X, Y, color='red', # 全部点设置为红色 marker='.', # 点的形状为圆点 linestyle='') # 线型为空,也即点与点之间不用线连接 plt.grid(True) plt.show()
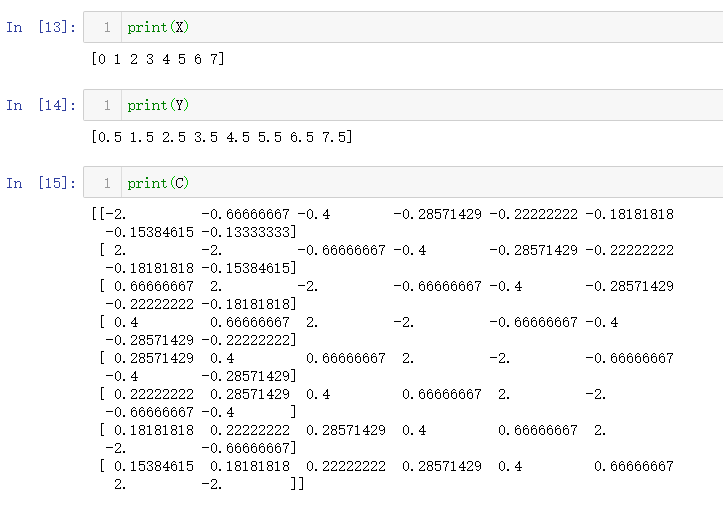
47. 给定两个数组 X 和 Y,构造柯西数组 C
$ C_{ij} =1 / (x_i - y_j)$
X = np.arange(8)
Y = X + 0.5
C = 1.0 / np.subtract.outer(X, Y)
💡
np.subtract.outer(X, Y)其含义是:有两个数组
a、b,要实现a中的每个元素与b中的每个元素进行比较例如:
import numpy as np a = np.array([5,6,7]) b = np.array([9,12,10]) np.subtract.outer(b,a) Out[11]: array([[4, 3, 2], [7, 6, 5], [5, 4, 3]])
48. 打印每种 numpy 标量类型的最小和最大可表示值 (★★☆)
for dtype in [np.int8, np.int32, np.int64]:
print(np.iinfo(dtype).min)
print(np.iinfo(dtype).max)
for dtype in [np.float32, np.float64]:
print(np.finfo(dtype).min)
print(np.finfo(dtype).max)
print(np.finfo(dtype).eps)

49. 打印数组的所有值 (★★☆)
np.set_printoptions(threshold=np.nan)
Z = np.zeros((16,16))
print(Z)
💡
np.set_printoptions设置打印选项,这些选项决定显示浮点数、数组和其他NumPy对象的方式。
np.set_printoptions(threshold = 1e6) # 设置打印数量的阈值,1e6 = 1000000.0 此方法为设置一较大值或
np.set_printoptions(threshold=np.nan) #全部输出
50. 如何在数组中找到最接近(给定标量)的值? (★★☆)
Z = np.arange(100)
v = np.random.uniform(0,100) # 在[0,100)的均匀分布中进行随机取样
print(v) # 45.05967943816573
index = (np.abs(Z-v)).argmin()
print(Z[index]) # 45
51. 创建一个表示位置(x,y)和颜色(r,g,b)的结构化数组 (★★☆)
Z = np.zeros(10, [ ('position', [ ('x', float, 1),
('y', float, 1)]),
('color', [ ('r', float, 1),
('g', float, 1),
('b', float, 1)])])
print(Z)
52. Consider a random vector with shape (100,2) representing coordinates, find point by point distances (★★☆)
Z = np.random.random((10,2))
X,Y = np.atleast_2d(Z[:,0], Z[:,1])
D = np.sqrt( (X-X.T)**2 + (Y-Y.T)**2)
print(D)
# Much faster with scipy
import scipy
# Thanks Gavin Heverly-Coulson (#issue 1)
import scipy.spatial
Z = np.random.random((10,2))
D = scipy.spatial.distance.cdist(Z,Z)
print(D)
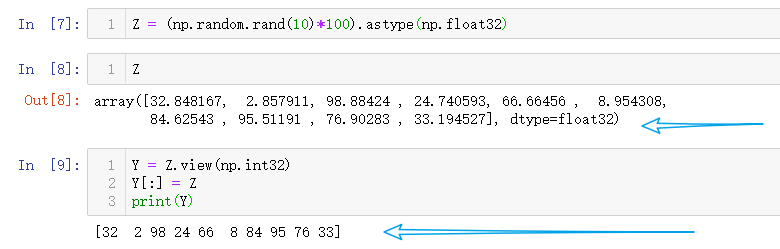
53. 如何将 32 位的浮点数 (float) 转换为对应的整数 (integer)?
Z = (np.random.rand(10)*100).astype(np.float32)
Y = Z.view(np.int32)
Y[:] = Z
print(Y)
54. How to read the following file? (★★☆)
1, 2, 3, 4, 5
6, , , 7, 8
, , 9,10,11
from io import StringIO
# Fake file
s = StringIO('''1, 2, 3, 4, 5
6, , , 7, 8
, , 9,10,11
''')
Z = np.genfromtxt(s, delimiter=",", dtype=np.int)
print(Z)
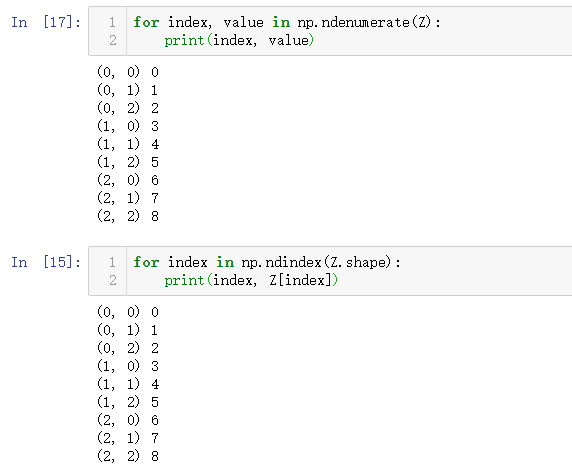
55. 对于numpy数组,enumerate的等价操作是什么? (★★☆)
Python 中的
enumerate()函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列,同时列出数据和数据下标,一般用在 for 循环当中。
Z = np.arange(9).reshape(3,3)
for index, value in np.ndenumerate(Z):
print(index, value)
# 或者
for index in np.ndindex(Z.shape):
print(index, Z[index])
56. Generate a generic 2D Gaussian-like array (★★☆)
X, Y = np.meshgrid(np.linspace(-1,1,10), np.linspace(-1,1,10))
D = np.sqrt(X*X+Y*Y)
sigma, mu = 1.0, 0.0
G = np.exp(-( (D-mu)**2 / ( 2.0 * sigma**2 ) ) )
print(G)
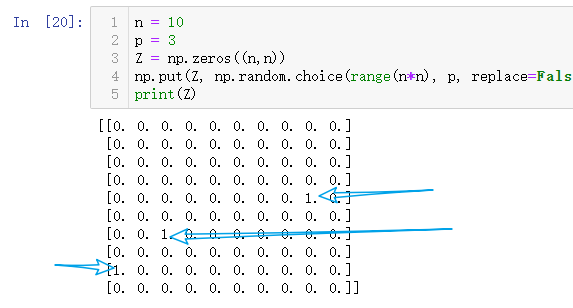
57. 对一个二维数组,如何在其内部随机放置p个元素? (★★☆)
n = 10
p = 3
Z = np.zeros((n,n))
np.put(Z, np.random.choice(range(n*n), p, replace=False),1)
print(Z)
💡:
np.put(a, ind, v, mode='raise')参数解释 :
a就是目标数组ind是目标数组的位置v是你要加入的值注意:在此函数中 a 是扁平化的(无论是一维还是二维)
举例
a = np.array([0,5,6,75,6]) np.put(a, [0, 2], [-44, -55]) # array([-44, 5, -55, 75, 6]) 就是把0和2位置上的值替换成了-44和-55
numpy.random.choice(a, size=None, replace=True, p=None)参数解释:
从
a(只要是ndarray都可以,但必须是一维的) 中随机抽取数字
size:取得数字的个数
replace:True表示可以取相同数字,False表示不可以取相同数字数组
p:描述数组a中每一个元素取得的概率。举例
np.random.choice(range(25),3,replace = False) # 从25的范围内取3个不同的数 # array([21, 4, 0])
58. 减去一个矩阵中的每一行的平均值 (★★☆)
X = np.random.rand(5, 10)
Y = X - X.mean(axis=1, keepdims=True)
print(Y)
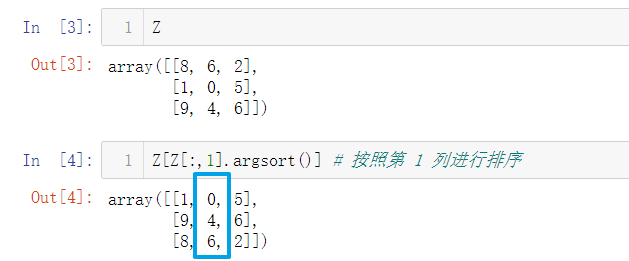
59. 按照第n列对一个数组进行排序 (★★☆)
Z = np.random.randint(0,10,(3,3))
print(Z)
print(Z[Z[:,1].argsort()]) # 按照第 1 列进行排序
60. 检查一个二维数组是否有空列 (★★☆)
Z = np.random.randint(0,3,(3,10))
print((~Z.any(axis=0)).any())
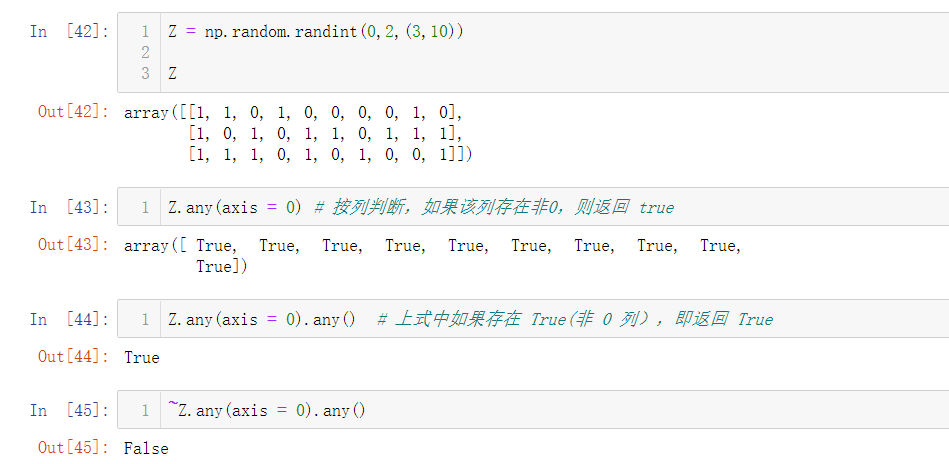
💡 函数说明:
np.all():判断该矩阵给定轴的所有元素是否都为True,非 0 即为 True
np.any():判断该矩阵给定轴的所有元素是否存在True,非 0 即为 True
61. Find the nearest value from a given value in an array (★★☆)
Z = np.random.uniform(0,1,10)
z = 0.5
m = Z.flat[np.abs(Z - z).argmin()]
print(m)
62. Considering two arrays with shape (1,3) and (3,1), how to compute their sum using an iterator? (★★☆)
A = np.arange(3).reshape(3,1)
B = np.arange(3).reshape(1,3)
it = np.nditer([A,B,None])
for x,y,z in it: z[...] = x + y
print(it.operands[2])
63. Create an array class that has a name attribute (★★☆)
class NamedArray(np.ndarray):
def __new__(cls, array, name="no name"):
obj = np.asarray(array).view(cls)
obj.name = name
return obj
def __array_finalize__(self, obj):
if obj is None: return
self.info = getattr(obj, 'name', "no name")
Z = NamedArray(np.arange(10), "range_10")
print (Z.name)
64. 考虑一个给定的向量,如何对由第二个向量索引的每个元素加 1 ? (★★★)
Z = np.ones(10)
I = np.random.randint(0,len(Z),20)
Z += np.bincount(I, minlength=len(Z))
print(Z)
# Another solution
np.add.at(Z, I, 1)
print(Z)

💡
np.add.at(x,[0,2],3)将 x 中下标为 0 和 2 的元素加上了 3
65. 根据索引列表(I),如何将向量(X)的元素累加到数组(F) ? (★★★)
X = [1,2,3,4,5,6]
I = [1,3,9,3,4,1]
F = np.bincount(I,X) # 将 X 向量中下标为 I 的元素
print(F)

💡
numpy.bincount频率统计函数:
numpy.bincount(x, weights=None, minlength=None): 将 x 中的元素进行分类,并汇总出现次数(如果给出了权重,就按照权重进行计算)比如:
np.bincount([0,0,1,3])输出是 [2 1 0 1],意思就是这个[0,0,1,3] 一共有 3 个值:0 1 3, 0 有 2 个,1 有 1 个,3 有 1 个,输出数组的下标即对应的值,所以输出就是[2 1 0 1]
66. Considering a (w,h,3) image of (dtype=ubyte), compute the number of unique colors (★★★)
# Author: Nadav Horesh
w,h = 16,16
I = np.random.randint(0,2,(h,w,3)).astype(np.ubyte)
F = I[...,0]*256*256 + I[...,1]*256 +I[...,2]
n = len(np.unique(F))
print(np.unique(I))
67. 考虑一个四维数组,如何一次性计算出最后两个轴(axis)的和? (★★★)
A = np.random.randint(0,10,(3,4,3,4))
# solution by passing a tuple of axes (introduced in numpy 1.7.0)
sum = A.sum(axis=(-2,-1))
print(sum)
# solution by flattening the last two dimensions into one
# (useful for functions that don't accept tuples for axis argument)
sum = A.reshape(A.shape[:-2] + (-1,)).sum(axis=-1)
print(sum)
68. Considering a one-dimensional vector D, how to compute means of subsets of D using a vector S of same size describing subset indices? (★★★)
# Author: Jaime Fernández del Río
D = np.random.uniform(0,1,100)
S = np.random.randint(0,10,100)
D_sums = np.bincount(S, weights=D)
D_counts = np.bincount(S)
D_means = D_sums / D_counts
print(D_means)
# Pandas solution as a reference due to more intuitive code
import pandas as pd
print(pd.Series(D).groupby(S).mean())
69. How to get the diagonal of a dot product? (★★★)
# Author: Mathieu Blondel
A = np.random.uniform(0,1,(5,5))
B = np.random.uniform(0,1,(5,5))
# Slow version
np.diag(np.dot(A, B))
# Fast version
np.sum(A * B.T, axis=1)
# Faster version
np.einsum("ij,ji->i", A, B)
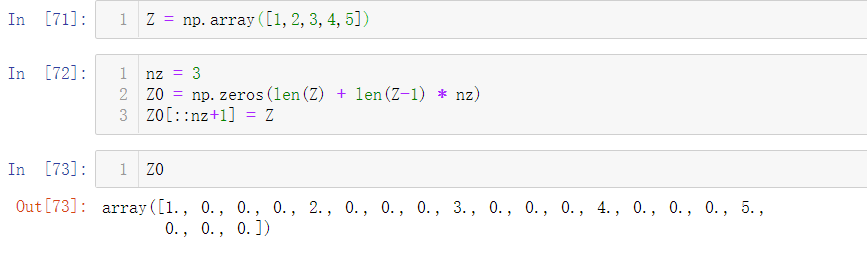
70. 考虑一个向量[1,2,3,4,5],如何建立一个新的向量,在这个新向量中每个值之间有3个连续的零? (★★★)
Z = np.array([1,2,3,4,5])
nz = 3
Z0 = np.zeros(len(Z) + (len(Z)-1)*(nz))
Z0[::nz+1] = Z
print(Z0)
71. 考虑一个维度(5,5,3)的数组,如何将其与一个(5,5)的数组相乘? (★★★)
A = np.ones((5,5,3))
B = 2*np.ones((5,5))
print(A * B[:,:,None]) # 相当于给 B 新增了一个维度

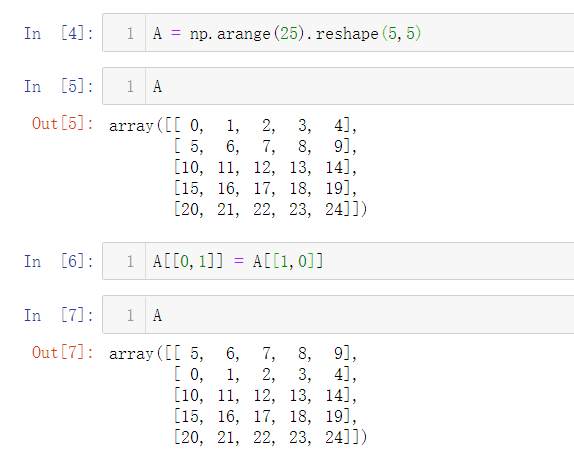
72. 如何对一个数组中任意两行做交换? (★★★)
A = np.arange(25).reshape(5,5)
A[[0,1]] = A[[1,0]]
print(A)
73. Consider a set of 10 triplets describing 10 triangles (with shared vertices), find the set of unique line segments composing all the triangles (★★★)
# Author: Nicolas P. Rougier
faces = np.random.randint(0,100,(10,3))
F = np.roll(faces.repeat(2,axis=1),-1,axis=1)
F = F.reshape(len(F)*3,2)
F = np.sort(F,axis=1)
G = F.view( dtype=[('p0',F.dtype),('p1',F.dtype)] )
G = np.unique(G)
print(G)
74. Given an array C that is a bincount, how to produce an array A such that np.bincount(A) == C? (★★★)
# Author: Jaime Fernández del Río
C = np.bincount([1,1,2,3,4,4,6])
A = np.repeat(np.arange(len(C)), C)
print(A)
75. How to compute averages using a sliding window over an array? (★★★)
# Author: Jaime Fernández del Río
def moving_average(a, n=3) :
ret = np.cumsum(a, dtype=float)
ret[n:] = ret[n:] - ret[:-n]
return ret[n - 1:] / n
Z = np.arange(20)
print(moving_average(Z, n=3))
76. Consider a one-dimensional array Z, build a two-dimensional array whose first row is (Z[0],Z[1],Z[2]) and each subsequent row is shifted by 1 (last row should be (Z[-3],Z[-2],Z[-1]) (★★★)
# Author: Joe Kington / Erik Rigtorp
from numpy.lib import stride_tricks
def rolling(a, window):
shape = (a.size - window + 1, window)
strides = (a.itemsize, a.itemsize)
return stride_tricks.as_strided(a, shape=shape, strides=strides)
Z = rolling(np.arange(10), 3)
print(Z)
77. How to negate a boolean, or to change the sign of a float inplace? (★★★)
# Author: Nathaniel J. Smith
Z = np.random.randint(0,2,100)
np.logical_not(Z, out=Z)
Z = np.random.uniform(-1.0,1.0,100)
np.negative(Z, out=Z)
78. Consider 2 sets of points P0,P1 describing lines (2d) and a point p, how to compute distance from p to each line i (P0[i],P1[i])? (★★★)
def distance(P0, P1, p):
T = P1 - P0
L = (T**2).sum(axis=1)
U = -((P0[:,0]-p[...,0])*T[:,0] + (P0[:,1]-p[...,1])*T[:,1]) / L
U = U.reshape(len(U),1)
D = P0 + U*T - p
return np.sqrt((D**2).sum(axis=1))
P0 = np.random.uniform(-10,10,(10,2))
P1 = np.random.uniform(-10,10,(10,2))
p = np.random.uniform(-10,10,( 1,2))
print(distance(P0, P1, p))
79. Consider 2 sets of points P0,P1 describing lines (2d) and a set of points P, how to compute distance from each point j (P[j]) to each line i (P0[i],P1[i])? (★★★)
# Author: Italmassov Kuanysh
# based on distance function from previous question
P0 = np.random.uniform(-10, 10, (10,2))
P1 = np.random.uniform(-10,10,(10,2))
p = np.random.uniform(-10, 10, (10,2))
print(np.array([distance(P0,P1,p_i) for p_i in p]))
80. Consider an arbitrary array, write a function that extract a subpart with a fixed shape and centered on a given element (pad with a fill value when necessary) (★★★)
# Author: Nicolas Rougier
Z = np.random.randint(0,10,(10,10))
shape = (5,5)
fill = 0
position = (1,1)
R = np.ones(shape, dtype=Z.dtype)*fill
P = np.array(list(position)).astype(int)
Rs = np.array(list(R.shape)).astype(int)
Zs = np.array(list(Z.shape)).astype(int)
R_start = np.zeros((len(shape),)).astype(int)
R_stop = np.array(list(shape)).astype(int)
Z_start = (P-Rs//2)
Z_stop = (P+Rs//2)+Rs%2
R_start = (R_start - np.minimum(Z_start,0)).tolist()
Z_start = (np.maximum(Z_start,0)).tolist()
R_stop = np.maximum(R_start, (R_stop - np.maximum(Z_stop-Zs,0))).tolist()
Z_stop = (np.minimum(Z_stop,Zs)).tolist()
r = [slice(start,stop) for start,stop in zip(R_start,R_stop)]
z = [slice(start,stop) for start,stop in zip(Z_start,Z_stop)]
R[r] = Z[z]
print(Z)
print(R)
81. Consider an array Z = [1,2,3,4,5,6,7,8,9,10,11,12,13,14], how to generate an array R = [[1,2,3,4], [2,3,4,5], [3,4,5,6], ..., [11,12,13,14]]? (★★★)
# Author: Stefan van der Walt
Z = np.arange(1,15,dtype=np.uint32)
R = stride_tricks.as_strided(Z,(11,4),(4,4))
print(R)
82. 计算一个矩阵的秩 (★★★)
Z = np.random.uniform(0,1,(10,10))
U, S, V = np.linalg.svd(Z) # Singular Value Decomposition
rank = np.sum(S > 1e-10)
print(rank)
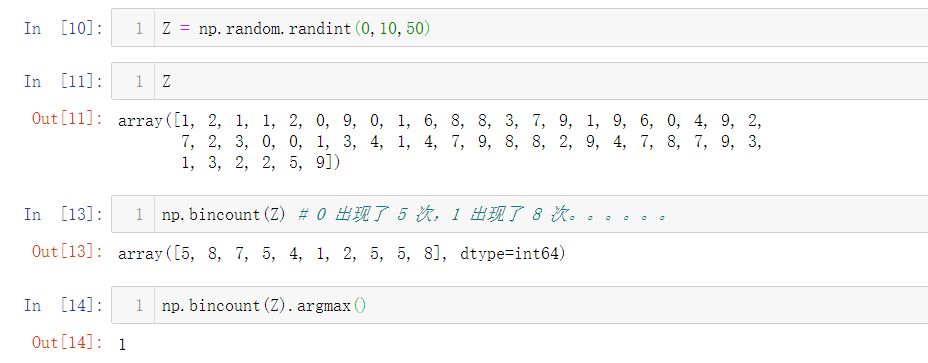
83. 如何找到一个数组中出现频率最高的值?
Z = np.random.randint(0,10,50)
print(np.bincount(Z).argmax())
84. Extract all the contiguous 3x3 blocks from a random 10x10 matrix (★★★)
# Author: Chris Barker
Z = np.random.randint(0,5,(10,10))
n = 3
i = 1 + (Z.shape[0]-3)
j = 1 + (Z.shape[1]-3)
C = stride_tricks.as_strided(Z, shape=(i, j, n, n), strides=Z.strides + Z.strides)
print(C)
85. Create a 2D array subclass such that Z[i,j] == Z[j,i] (★★★)
# Author: Eric O. Lebigot
# Note: only works for 2d array and value setting using indices
class Symetric(np.ndarray):
def __setitem__(self, index, value):
i,j = index
super(Symetric, self).__setitem__((i,j), value)
super(Symetric, self).__setitem__((j,i), value)
def symetric(Z):
return np.asarray(Z + Z.T - np.diag(Z.diagonal())).view(Symetric)
S = symetric(np.random.randint(0,10,(5,5)))
S[2,3] = 42
print(S)
86. Consider a set of p matrices wich shape (n,n) and a set of p vectors with shape (n,1). How to compute the sum of of the p matrix products at once? (result has shape (n,1)) (★★★)
# Author: Stefan van der Walt
p, n = 10, 20
M = np.ones((p,n,n))
V = np.ones((p,n,1))
S = np.tensordot(M, V, axes=[[0, 2], [0, 1]])
print(S)
# It works, because:
# M is (p,n,n)
# V is (p,n,1)
# Thus, summing over the paired axes 0 and 0 (of M and V independently),
# and 2 and 1, to remain with a (n,1) vector.
87. Consider a 16x16 array, how to get the block-sum (block size is 4x4)? (★★★)
# Author: Robert Kern
Z = np.ones((16,16))
k = 4
S = np.add.reduceat(np.add.reduceat(Z, np.arange(0, Z.shape[0], k), axis=0),
np.arange(0, Z.shape[1], k), axis=1)
print(S)
88. How to implement the Game of Life using numpy arrays? (★★★)
# Author: Nicolas Rougier
def iterate(Z):
# Count neighbours
N = (Z[0:-2,0:-2] + Z[0:-2,1:-1] + Z[0:-2,2:] +
Z[1:-1,0:-2] + Z[1:-1,2:] +
Z[2: ,0:-2] + Z[2: ,1:-1] + Z[2: ,2:])
# Apply rules
birth = (N==3) & (Z[1:-1,1:-1]==0)
survive = ((N==2) | (N==3)) & (Z[1:-1,1:-1]==1)
Z[...] = 0
Z[1:-1,1:-1][birth | survive] = 1
return Z
Z = np.random.randint(0,2,(50,50))
for i in range(100): Z = iterate(Z)
print(Z)
89. How to get the n largest values of an array (★★★)
Z = np.arange(10000)
np.random.shuffle(Z)
n = 5
# Slow
print (Z[np.argsort(Z)[-n:]])
# Fast
print (Z[np.argpartition(-Z,n)[:n]])
90. Given an arbitrary number of vectors, build the cartesian product (every combinations of every item) (★★★)
# Author: Stefan Van der Walt
def cartesian(arrays):
arrays = [np.asarray(a) for a in arrays]
shape = (len(x) for x in arrays)
ix = np.indices(shape, dtype=int)
ix = ix.reshape(len(arrays), -1).T
for n, arr in enumerate(arrays):
ix[:, n] = arrays[n][ix[:, n]]
return ix
print (cartesian(([1, 2, 3], [4, 5], [6, 7])))
91. How to create a record array from a regular array? (★★★)
Z = np.array([("Hello", 2.5, 3),
("World", 3.6, 2)])
R = np.core.records.fromarrays(Z.T,
names='col1, col2, col3',
formats = 'S8, f8, i8')
print(R)
92. Consider a large vector Z, compute Z to the power of 3 using 3 different methods (★★★)
# Author: Ryan G.
x = np.random.rand(int(5e7))
%timeit np.power(x,3)
%timeit x*x*x
%timeit np.einsum('i,i,i->i',x,x,x)
93. Consider two arrays A and B of shape (8,3) and (2,2). How to find rows of A that contain elements of each row of B regardless of the order of the elements in B? (★★★)
# Author: Gabe Schwartz
A = np.random.randint(0,5,(8,3))
B = np.random.randint(0,5,(2,2))
C = (A[..., np.newaxis, np.newaxis] == B)
rows = np.where(C.any((3,1)).all(1))[0]
print(rows)
94. Considering a 10x3 matrix, extract rows with unequal values (e.g. [2,2,3]) (★★★)
# Author: Robert Kern
Z = np.random.randint(0,5,(10,3))
print(Z)
# solution for arrays of all dtypes (including string arrays and record arrays)
E = np.all(Z[:,1:] == Z[:,:-1], axis=1)
U = Z[~E]
print(U)
# soluiton for numerical arrays only, will work for any number of columns in Z
U = Z[Z.max(axis=1) != Z.min(axis=1),:]
print(U)
95. Convert a vector of ints into a matrix binary representation (★★★)
# Author: Warren Weckesser
I = np.array([0, 1, 2, 3, 15, 16, 32, 64, 128])
B = ((I.reshape(-1,1) & (2**np.arange(8))) != 0).astype(int)
print(B[:,::-1])
# Author: Daniel T. McDonald
I = np.array([0, 1, 2, 3, 15, 16, 32, 64, 128], dtype=np.uint8)
print(np.unpackbits(I[:, np.newaxis], axis=1))
96. Given a two dimensional array, how to extract unique rows? (★★★)
# Author: Jaime Fernández del Río
Z = np.random.randint(0,2,(6,3))
T = np.ascontiguousarray(Z).view(np.dtype((np.void, Z.dtype.itemsize * Z.shape[1])))
_, idx = np.unique(T, return_index=True)
uZ = Z[idx]
print(uZ)
# Author: Andreas Kouzelis
# NumPy >= 1.13
uZ = np.unique(Z, axis=0)
print(uZ)
97. Considering 2 vectors A & B, write the einsum equivalent of inner, outer, sum, and mul function (★★★)
# Author: Alex Riley
# Make sure to read: http://ajcr.net/Basic-guide-to-einsum/
A = np.random.uniform(0,1,10)
B = np.random.uniform(0,1,10)
np.einsum('i->', A) # np.sum(A)
np.einsum('i,i->i', A, B) # A * B
np.einsum('i,i', A, B) # np.inner(A, B)
np.einsum('i,j->ij', A, B) # np.outer(A, B)
98. Considering a path described by two vectors (X,Y), how to sample it using equidistant samples (★★★)?
# Author: Bas Swinckels
phi = np.arange(0, 10*np.pi, 0.1)
a = 1
x = a*phi*np.cos(phi)
y = a*phi*np.sin(phi)
dr = (np.diff(x)**2 + np.diff(y)**2)**.5 # segment lengths
r = np.zeros_like(x)
r[1:] = np.cumsum(dr) # integrate path
r_int = np.linspace(0, r.max(), 200) # regular spaced path
x_int = np.interp(r_int, r, x) # integrate path
y_int = np.interp(r_int, r, y)
99. Given an integer n and a 2D array X, select from X the rows which can be interpreted as draws from a multinomial distribution with n degrees, i.e., the rows which only contain integers and which sum to n. (★★★)
# Author: Evgeni Burovski
X = np.asarray([[1.0, 0.0, 3.0, 8.0],
[2.0, 0.0, 1.0, 1.0],
[1.5, 2.5, 1.0, 0.0]])
n = 4
M = np.logical_and.reduce(np.mod(X, 1) == 0, axis=-1)
M &= (X.sum(axis=-1) == n)
print(X[M])
100. Compute bootstrapped 95% confidence intervals for the mean of a 1D array X (i.e., resample the elements of an array with replacement N times, compute the mean of each sample, and then compute percentiles over the means). (★★★)
# Author: Jessica B. Hamrick
X = np.random.randn(100) # random 1D array
N = 1000 # number of bootstrap samples
idx = np.random.randint(0, X.size, (N, X.size))
means = X[idx].mean(axis=1)
confint = np.percentile(means, [2.5, 97.5])
print(confint)
📚 References
- Github - numpy - 100
- Numpy练习题100题-提高你的数据分析技能
- numpy.eye()函数
- numpy中pad函数的常用方法
- 图解Numpy的tile函数
- 具有自动域的数学函数( numpy.emath / numpy.lib.scimath)
- Numpy库基础分析——详解datetime类型的处理
- python中numpy.zeros(np.zeros)的使用方法
- numpy.meshgrid()理解
- np.subtract.outer()
- 菜鸟教程 — Python enumerate() 函数
- python numpy函数问题np.put和np.random.choice()
- Python NumPy.all()与any()函数理解
- np.add
- np.bincount()频率统计函数


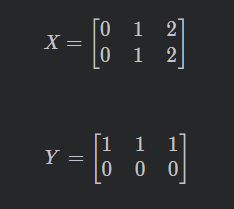


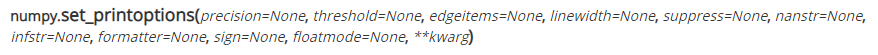


 浙公网安备 33010602011771号
浙公网安备 33010602011771号