java实现各种排序算法(比较排序)
准备
public interface Sort {
void sort(int[] nums);
}
定义所有排序方式通用接口
冒泡排序
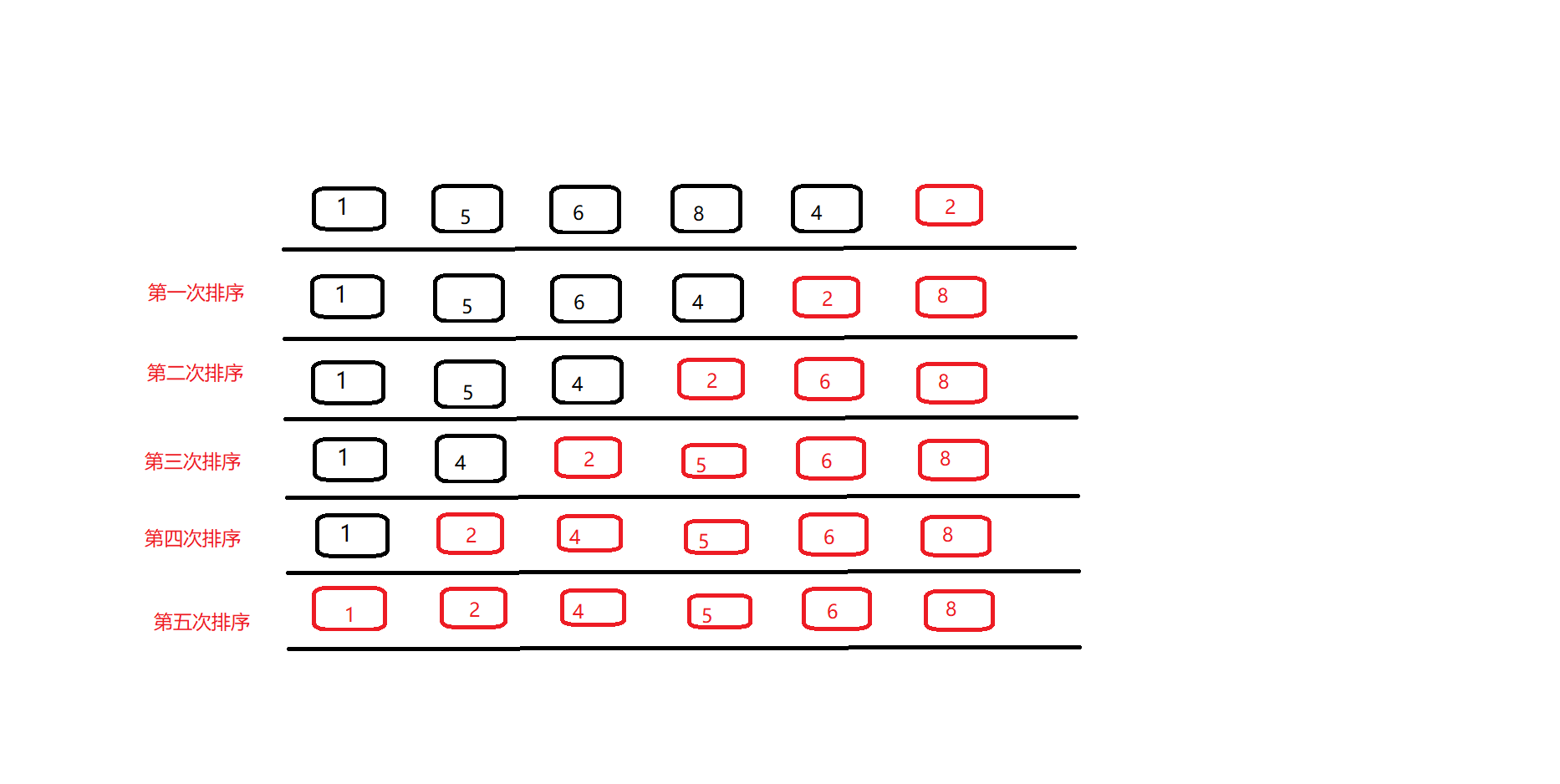
两两比较,将最大(最小值)移动到最右边。
第一版
public class BubbleSort implements Sort {
@Override
public void sort(int[] nums) {
//[i,len)为已排序
for (int i = nums.length - 1; i > 0; i--) {
for (int j = 0; j < i; j++) {
if (nums[j] > nums[j + 1]) {
swap(nums, j, j + 1);
}
}
}
}
private void swap(int[] nums, int left, int right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
}
第二版
相对于第一版,在已经有序的情况下直接结束,后面不用比较了。
public class BubbleSort2 implements Sort {
@Override
public void sort(int[] nums) {
//[i,len)为已排序
for (int i = nums.length - 1; i > 0; i--) {
boolean sorted = true;
for (int j = 0; j < i; j++) {
if (nums[j] > nums[j + 1]) {
swap(nums, j, j + 1);
sorted = false;
}
}
if (sorted) {
break;
}
}
}
private void swap(int[] nums, int left, int right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
}
第三版
和第二版类似,记录最后一次的交换位置,交换位置之后的都可以算作排好序了。
public class BubbleSort3 implements Sort {
@Override
public void sort(int[] nums) {
//[i,len)为已排序
for (int i = nums.length - 1; i > 0; ) {
//记录最后一次交换的位置
int lastSwappedIndex = 0;
for (int j = 0; j < i; j++) {
if (nums[j] > nums[j + 1]) {
swap(nums, j, j + 1);
lastSwappedIndex = j + 1;
}
}
i = lastSwappedIndex;
}
}
private void swap(int[] nums, int left, int right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
}
选择排序
每次找到待排序数组中最小或最大的元素放到已排序数组中
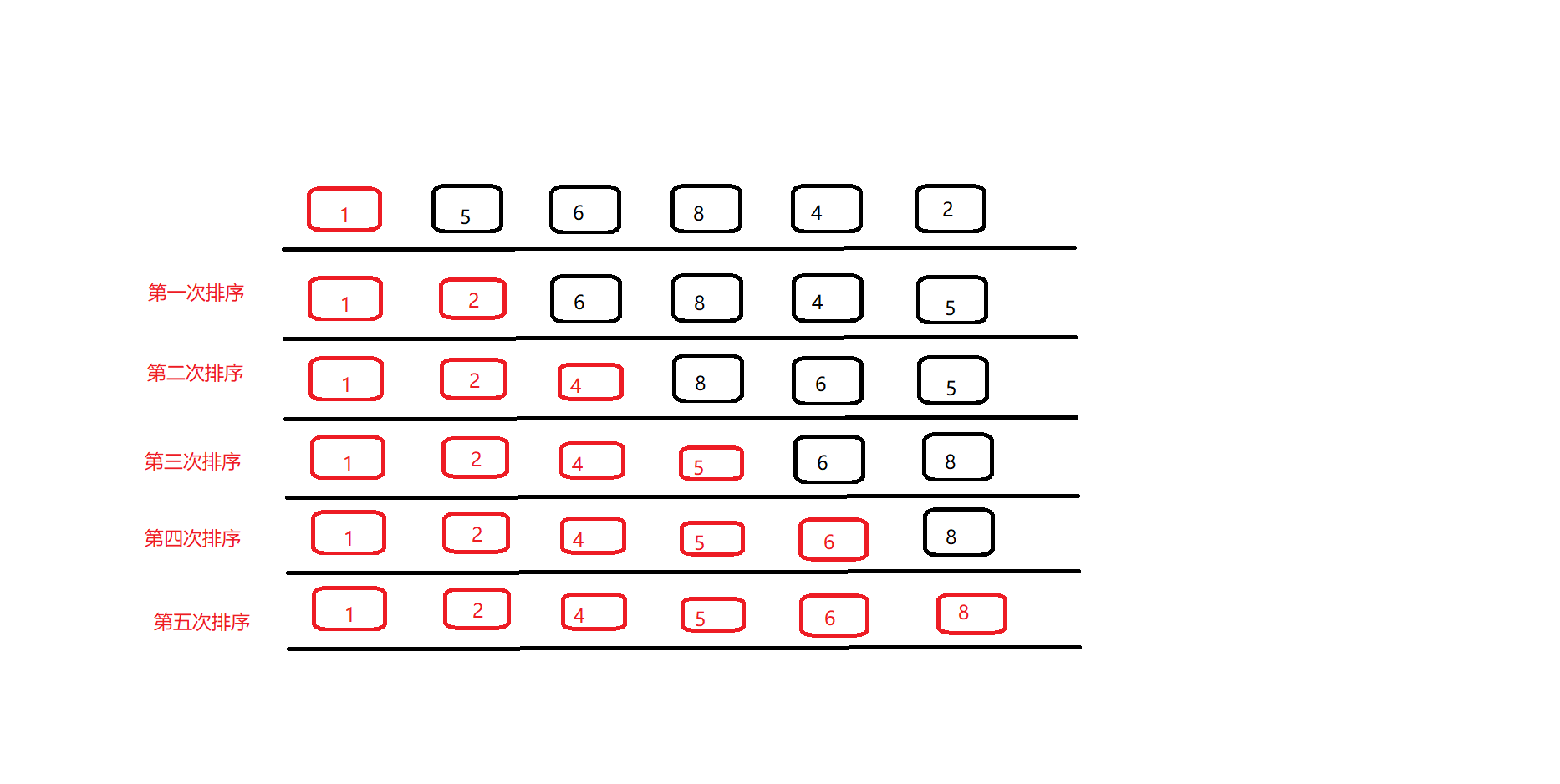
红色表示已排序
public class SelectSort implements Sort {
private void swap(int[] nums, int left, int right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
@Override
public void sort(int[] nums) {
//[0,i)为已排序的,[i,n)为未排序的
for (int i = 0; i < nums.length; i++) {
int minIndex = i;
for (int j = minIndex; j < nums.length; j++) {
if (nums[j] < nums[minIndex]) {
minIndex = j;
}
}
swap(nums, i, minIndex);
}
}
}
插入排序
每次将待排序元素插入到已排序数组中适当的位置
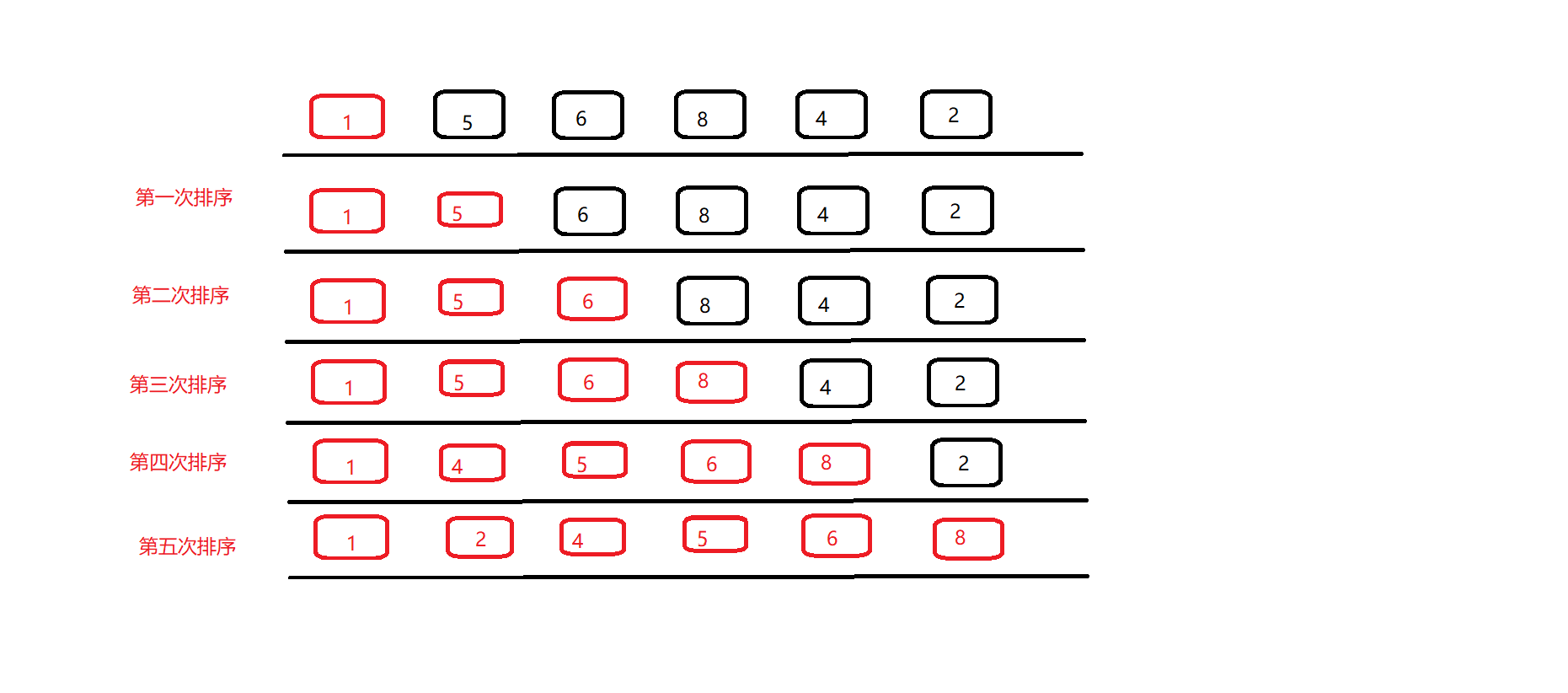
public class InsertSort implements Sort {
@Override
public void sort(int[] nums) {
//[0,i+1)为已排序的,[i+1,n)为未排序的
for (int i = 0; i < nums.length - 1; i++) {
int insertValue = nums[i + 1];
int j = i;
while (j >= 0 && insertValue < nums[j]) {
nums[j + 1] = nums[j];
j--;
}
nums[j + 1] = insertValue;
}
}
}
插入排序在数组元素接近有序的情况下有更好的性能。
希尔排序
希尔排序可以看做增强版的插入排序,每次对不同间隔的数组区间进行插入排序。
第一版
public class ShellSort implements Sort {
@Override
public void sort(int[] nums) {
int h = 1;
while (h < nums.length) {
h = h * 3 + 1;
}
while (h > 0) {
//对len/h个小数组排序
for (int start = 0; start < h; start++) {
//对[start,start+h,start+2h...]排序
for (int i = start + h; i < nums.length; i += h) {
int insertValue = nums[i];
int j = i - h;
while (j >= 0 && insertValue < nums[j]) {
nums[j + h] = nums[j];
j -= h;
}
nums[j + h] = insertValue;
}
}
h /= 3;
}
}
}
第二版
将4个循环优化成3个循环
public class ShellSort2 implements Sort {
@Override
public void sort(int[] nums) {
int h = 1;
while (h < nums.length) {
h = h * 3 + 1;
}
while (h > 0) {
//对[h,len]排序
for (int i = h; i < nums.length; i++) {
int insertValue = nums[i];
int j = i - h;
while (j >= 0 && insertValue < nums[j]) {
nums[j + h] = nums[j];
j -= h;
}
nums[j + h] = insertValue;
}
h /= 3;
}
}
}
归并排序
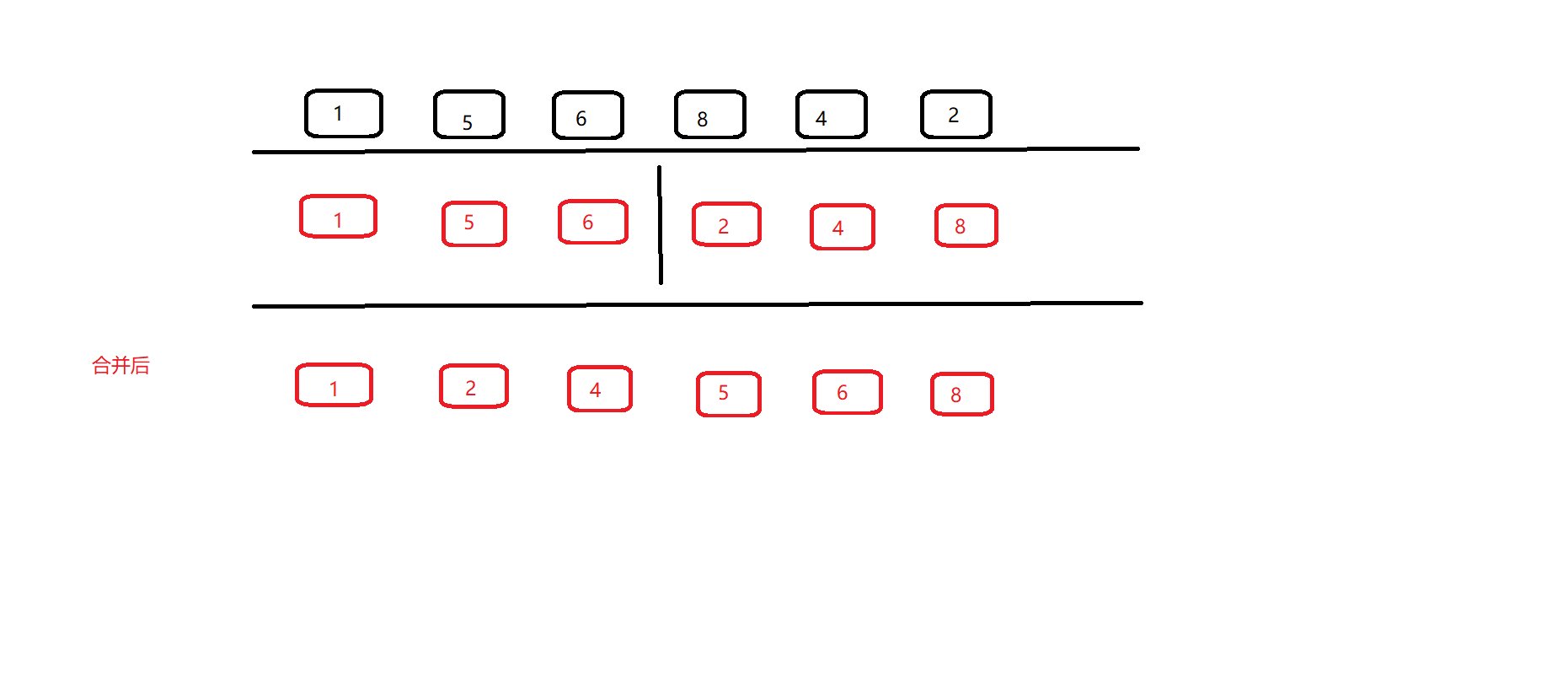
自顶向下递归实现
public class MergeSort implements Sort {
@Override
public void sort(int[] nums) {
int[] temp = new int[nums.length];
mergeSort(nums, temp, 0, nums.length - 1);
}
private void mergeSort(int[] nums, int[] temp, int left, int right) {
if (left >= right) {
return;
}
int middle = left + ((right - left) >> 1);
mergeSort(nums, temp, left, middle);
mergeSort(nums, temp, middle + 1, right);
//如果已经有序,不merge
if (nums[middle] > nums[middle + 1]) {
merge(nums, temp, left, middle, right);
}
}
//数组[left,middle]和[middle+1,right]都是已排序的,合并两个区间
private void merge(int[] nums, int[] temp, int left, int middle, int right) {
int leftIndex = left;
int rightIndex = middle + 1;
int tempIndex = 0;
while (leftIndex <= middle && rightIndex <= right) {
if (nums[leftIndex] <= nums[rightIndex]) {
temp[tempIndex++] = nums[leftIndex++];
} else {
temp[tempIndex++] = nums[rightIndex++];
}
}
while (leftIndex <= middle) {
temp[tempIndex++] = nums[leftIndex++];
}
while (rightIndex <= right) {
temp[tempIndex++] = nums[rightIndex++];
}
System.arraycopy(temp, 0, nums, left, right - left + 1);
}
}
自底向上循环实现
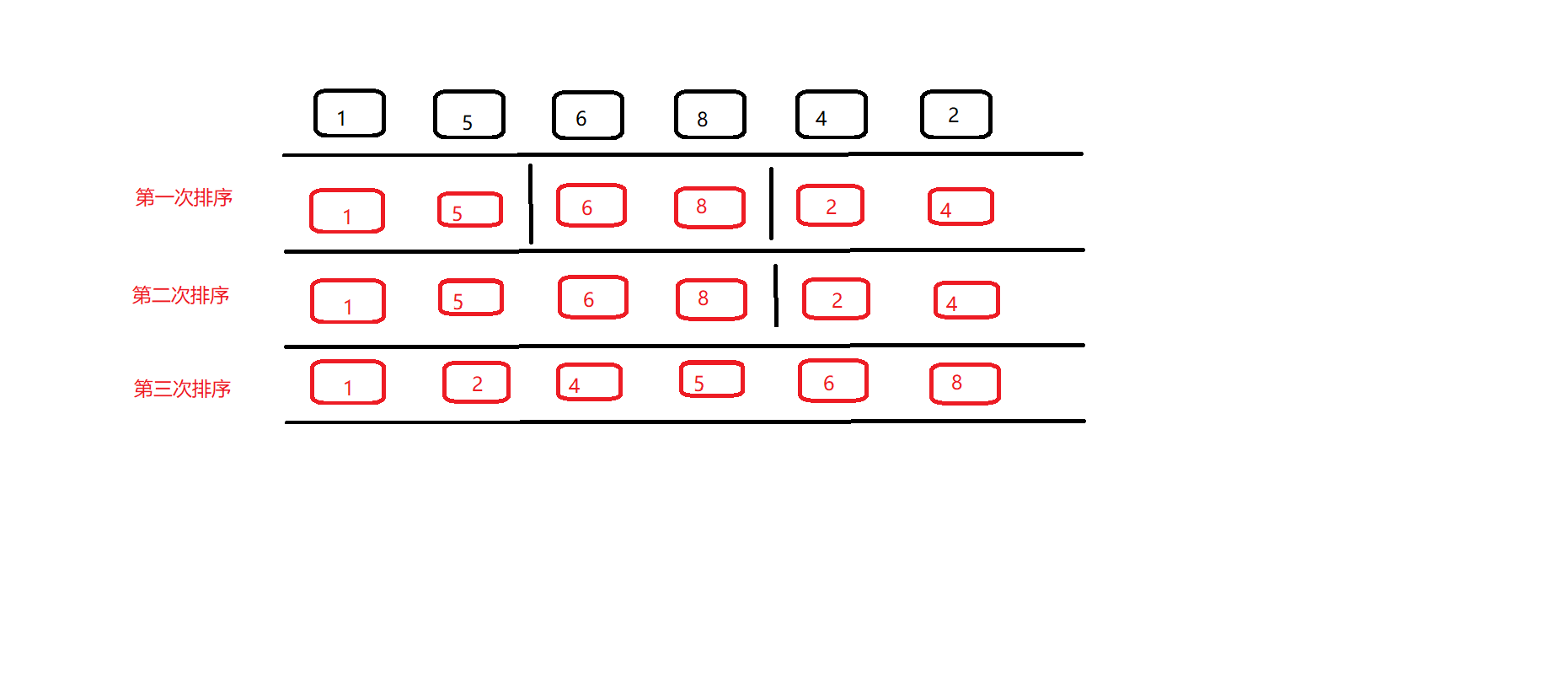
public class MergeSort2 implements Sort {
//数组[left,middle]和[middle+1,right]都是已排序的,合并两个区间
private void merge(int[] nums, int[] temp, int left, int middle, int right) {
int leftIndex = left;
int rightIndex = middle + 1;
int tempIndex = 0;
while (leftIndex <= middle && rightIndex <= right) {
if (nums[leftIndex] <= nums[rightIndex]) {
temp[tempIndex++] = nums[leftIndex++];
} else {
temp[tempIndex++] = nums[rightIndex++];
}
}
while (leftIndex <= middle) {
temp[tempIndex++] = nums[leftIndex++];
}
while (rightIndex <= right) {
temp[tempIndex++] = nums[rightIndex++];
}
System.arraycopy(temp, 0, nums, left, right - left + 1);
}
@Override
public void sort(int[] nums) {
int len = nums.length;
int[] temp = new int[len];
for (int sz = 1; sz < len; sz += sz) {
for (int i = 0; i < len - sz; i += sz + sz) {
int middle = i + sz - 1;
int right = Math.min(i + sz + sz - 1, len - 1);
if (nums[middle] > nums[middle + 1]) {
merge(nums, temp, i, middle, right);
}
}
}
}
}
归并排序的一个应用
快速排序
单路快排
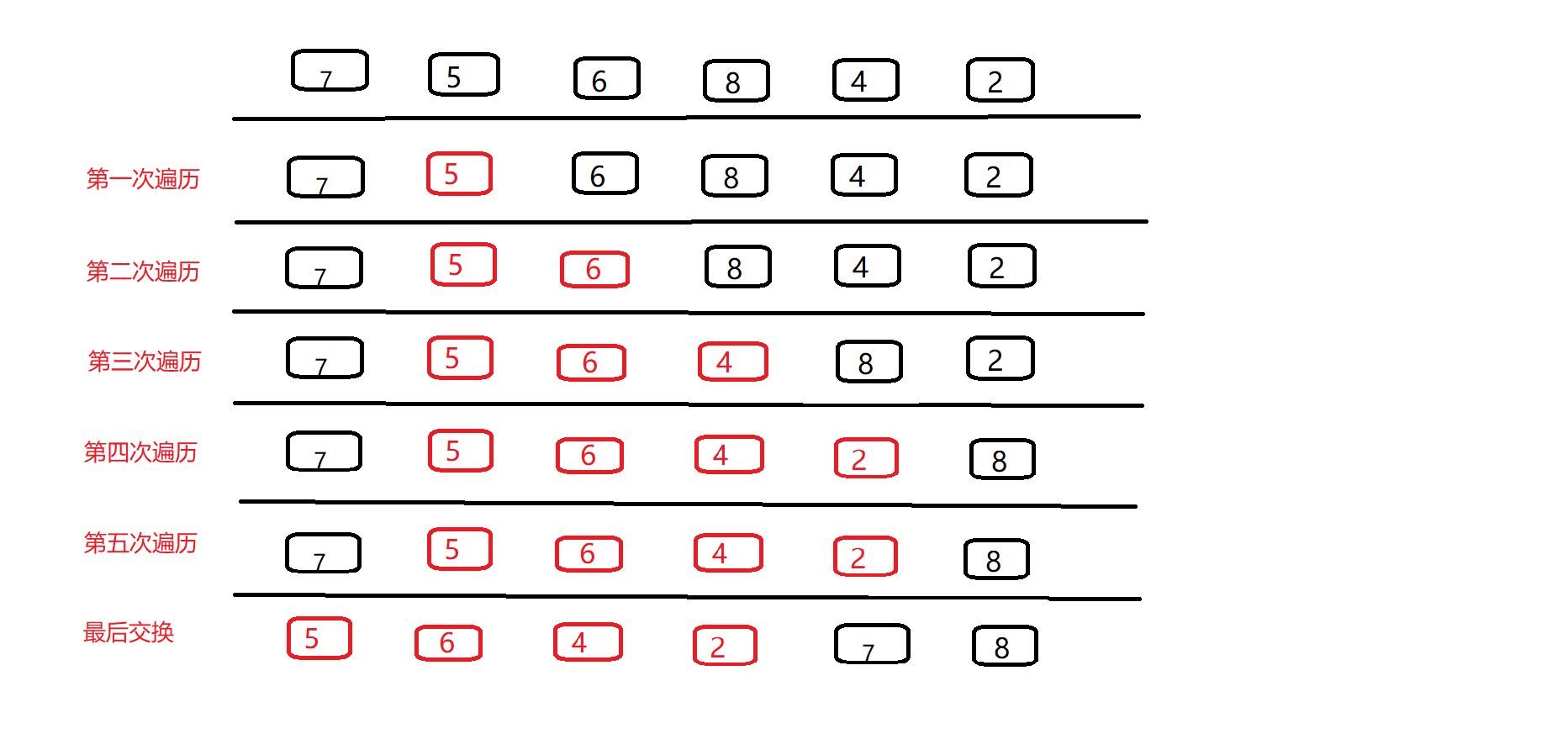
上图为分割的过程,基准值为左边第一个7,返回的分割点为索引下标4
public class QuickSort implements Sort {
private void quickSort(int[] nums, int left, int right) {
if (left >= right) {
return;
}
int p = partition(nums, left, right);
quickSort(nums, left, p - 1);
quickSort(nums, p + 1, right);
}
private int partition(int[] nums, int left, int right) {
int pivot = nums[left];
int leftIndex = left;
int rightIndex = left + 1;
//[left+1,leftIndex] < pivot [leftIndex+1,rightIndex] >= pivot
while (rightIndex <= right) {
if (nums[rightIndex] < pivot) {
leftIndex++;
swap(nums, leftIndex, rightIndex);
}
rightIndex++;
}
swap(nums, left, leftIndex);
return leftIndex;
}
private void swap(int[] nums, int left, int right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
@Override
public void sort(int[] nums) {
quickSort(nums, 0, nums.length - 1);
}
}
第一种方式在数据已经有序的情况下会退化成O(n^2)的时间复杂度。我们可以通过随机选取基准值来优化
import java.util.Random;
public class QuickSort1 implements Sort {
private void quickSort(int[] nums, int left, int right, Random random) {
if (left >= right) {
return;
}
int p = partition(nums, left, right, random);
quickSort(nums, left, p - 1, random);
quickSort(nums, p + 1, right, random);
}
private int partition(int[] nums, int left, int right, Random random) {
int pivotIndex = random.nextInt(right - left + 1) + left;
swap(nums, pivotIndex, left);
int pivot = nums[left];
int leftIndex = left;
int rightIndex = left;
//[left+1,leftIndex] < pivot [leftIndex+1,rightIndex] >= pivot
while (rightIndex <= right) {
if (nums[rightIndex] < pivot) {
leftIndex++;
swap(nums, leftIndex, rightIndex);
}
rightIndex++;
}
swap(nums, left, leftIndex);
return leftIndex;
}
private void swap(int[] nums, int left, int right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
@Override
public void sort(int[] nums) {
Random random = new Random();
quickSort(nums, 0, nums.length - 1, random);
}
}
上面这种实现在数据都相同的情况下还是会退化成O(n^2),我们可以使用双路快排优化。
双路快排
import java.util.Random;
public class QuickSort2 implements Sort {
private void quickSort(int[] nums, int left, int right, Random random) {
if (left >= right) {
return;
}
int p = partition(nums, left, right, random);
quickSort(nums, left, p - 1, random);
quickSort(nums, p + 1, right, random);
}
private int partition(int[] nums, int left, int right, Random random) {
int pivotIndex = random.nextInt(right - left + 1) + left;
swap(nums, pivotIndex, left);
int pivot = nums[left];
int leftIndex = left + 1;
int rightIndex = right;
//[left+1,leftIndex-1] <= pivot [rightIndex+1,right] >= pivot
while (true) {
while (leftIndex <= rightIndex && nums[leftIndex] < pivot) {
leftIndex++;
}
while (leftIndex <= rightIndex && nums[rightIndex] > pivot) {
rightIndex--;
}
if (leftIndex >= rightIndex) {
break;
}
swap(nums, leftIndex, rightIndex);
leftIndex++;
rightIndex--;
}
swap(nums, left, rightIndex);
return rightIndex;
}
private void swap(int[] nums, int left, int right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
@Override
public void sort(int[] nums) {
Random random = new Random();
quickSort(nums, 0, nums.length - 1, random);
}
}
从左边找到大于等于基准值的索引,右边找到小于等于基准值的索引,交换,循环这个过程直到数组结束。双路快排在随机数组,有序数组,元素相同的数组中都会有很好地性能。
三路快排
import java.util.Random;
public class QuickSort3 implements Sort {
private void quickSort(int[] nums, int left, int right, Random random) {
if (left >= right) {
return;
}
int[] p = partition(nums, left, right, random);
quickSort(nums, left, p[0], random);
quickSort(nums, p[1], right, random);
}
private int[] partition(int[] nums, int left, int right, Random random) {
int pivotIndex = random.nextInt(right - left + 1) + left;
swap(nums, pivotIndex, left);
int pivot = nums[left];
int leftIndex = left;
int rightIndex = right + 1;
int cur = left + 1;
//[left+1,leftIndex]<pivot [leftIndex+1,cur-1]=pivot [rightIndex,right]>pivot
while (cur < rightIndex) {
if (nums[cur] < pivot) {
leftIndex++;
swap(nums, cur, leftIndex);
cur++;
} else if (nums[cur] > pivot) {
rightIndex--;
swap(nums, cur, rightIndex);
} else {
cur++;
}
}
swap(nums, left, leftIndex);
//[left,leftIndex-1]<pivot [leftIndex,rightIndex-1]=pivot [rightIndex,right]>pivot
return new int[]{leftIndex - 1, rightIndex};
}
private void swap(int[] nums, int left, int right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
@Override
public void sort(int[] nums) {
Random random = new Random();
quickSort(nums, 0, nums.length - 1, random);
}
}
三路快排将数组分成3部分,小于基准值的,等于基准值的,大于基准值的,下一次递归时直接从小于和大于开始,相比双路快排,在数组中包含大量相同元素时有更好的性能。如果元素全部相同,时间复杂度就是O(n)。
三路快排的一个应用
分割思想的一个应用
堆排序
实现堆这种数据结构,更多关于堆请看 java实现堆数据结构
/**
* 实现一个最大堆
*/
public class MaxHeap<E extends Comparable<E>> {
private List<E> delegate;
public MaxHeap() {
delegate = new ArrayList<>();
}
public MaxHeap(E[] source) {
delegate = new ArrayList<>(Arrays.asList(source));
heapify();
}
/**
* 添加元素
*/
public void add(E e) {
delegate.add(e);
siftUp(size() - 1, e);
}
/**
* 查看最大值元素
*/
public E peek() {
rangeCheck();
return delegate.get(0);
}
/**
* 删除最大值元素
*/
public E poll() {
rangeCheck();
swap(0, size() - 1);
E removeEle = delegate.remove(size() - 1);
siftDown(0);
return removeEle;
}
/**
* 使用新元素替换最大值
*/
public E replace(E e) {
rangeCheck();
E oldEle = delegate.get(0);
delegate.set(0, e);
siftDown(0);
return oldEle;
}
/**
* 将非堆的结构转换成堆结构
*/
private void heapify() {
int size = parent(size() - 1);
for (int i = size; i >= 0; i--) {
siftDown(i);
}
}
/**
* 堆是否为空
*/
public boolean isEmpty() {
return delegate.isEmpty();
}
/**
* 堆容量
*/
public int size() {
return delegate.size();
}
@Override
public String toString() {
return delegate.toString();
}
private void siftUp(int index, E e) {
int cur = index;
while (cur > 0) {
int parentIndex = parent(cur);
E childEle = delegate.get(cur);
E parentEle = delegate.get(parentIndex);
//当前节点大于父节点才交换
if (childEle.compareTo(parentEle) <= 0) {
break;
}
swap(cur, parentIndex);
cur = parentIndex;
}
}
private void siftDown(int index) {
int size = size();
int cur = index;
while (true) {
int leftIndex = leftChild(cur);
//没有左孩子
if (leftIndex >= size) {
break;
}
int rightIndex = rightChild(cur);
E curEle = delegate.get(cur);
E maxChild = delegate.get(leftIndex);
int maxChildIndex = leftIndex;
//存在右孩子且右孩子大于左孩子
if (rightIndex < size) {
E rightEle = delegate.get(rightIndex);
if (rightEle.compareTo(maxChild) > 0) {
maxChildIndex = rightIndex;
maxChild = rightEle;
}
}
if (maxChild.compareTo(curEle) <= 0) {
break;
}
//将当前节点和左右孩子中的最大节点交换
swap(cur, maxChildIndex);
cur = maxChildIndex;
}
}
private void rangeCheck() {
if (isEmpty()) {
throw new IllegalArgumentException("heap is empty.");
}
}
private void swap(int left, int right) {
E temp = delegate.get(left);
delegate.set(left, delegate.get(right));
delegate.set(right, temp);
}
private int parent(int index) {
return (index - 1) / 2;
}
private int leftChild(int index) {
return index * 2 + 1;
}
private int rightChild(int index) {
return index * 2 + 2;
}
}
非原地排序
public class HeapSort implements Sort {
@Override
public void sort(int[] nums) {
MaxHeap<Integer> heap = new MaxHeap<>();
for (int num : nums) {
heap.add(num);
}
for (int i = nums.length - 1; i >= 0; i--) {
nums[i] = heap.poll();
}
}
}
原地排序
创建一个int类型的最大堆
import java.util.Arrays;
/**
* 实现一个最大堆
*/
public class IntMaxHeap {
private int[] data;
public IntMaxHeap(int[] source) {
data = source;
heapify();
}
/**
* 将非堆的结构转换成堆结构
*/
private void heapify() {
int size = size();
int lastParent = parent(size - 1);
for (int i = lastParent; i >= 0; i--) {
siftDown(i, size);
}
}
public void sort() {
int size = size();
for (int i = size - 1; i >= 0; i--) {
swap(0, i);
siftDown(0, i);
}
}
/**
* 堆容量
*/
public int size() {
return data.length;
}
public String toString() {
return Arrays.toString(data);
}
private void siftDown(int index, int size) {
int cur = index;
while (true) {
int leftIndex = leftChild(cur);
//没有左孩子
if (leftIndex >= size) {
break;
}
int rightIndex = rightChild(cur);
int curEle = data[cur];
int maxChild = data[leftIndex];
int maxChildIndex = leftIndex;
//存在右孩子且右孩子大于左孩子
if (rightIndex < size) {
int rightEle = data[rightIndex];
if (rightEle > maxChild) {
maxChildIndex = rightIndex;
maxChild = rightEle;
}
}
if (maxChild <= curEle) {
break;
}
//将当前节点和左右孩子中的最大节点交换
swap(cur, maxChildIndex);
cur = maxChildIndex;
}
}
private void swap(int left, int right) {
int temp = data[left];
data[left] = data[right];
data[right] = temp;
}
private int parent(int index) {
return (index - 1) / 2;
}
private int leftChild(int index) {
return index * 2 + 1;
}
private int rightChild(int index) {
return index * 2 + 2;
}
}
public class HeapSort2 implements Sort {
@Override
public void sort(int[] nums) {
IntMaxHeap heap = new IntMaxHeap(nums);
heap.sort();
}
}
总结
| 平均时间复杂度 | 最好 | 最坏 | 空间复杂度 | 稳定性 | |
|---|---|---|---|---|---|
| 冒泡排序 | O(n^2) | O(n) | O(n^2) | O(1) | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 插入排序 | O(n^2) | O(n) | O(n^2) | O(1) | 稳定 |
| 希尔排序 | O(nlogn)~O(n^2) | O(nlogn)~O(n^2) | O(nlogn)~O(n^2) | O(1) | 不稳定 |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 |
| 快速排序 | O(nlogn) | O(n) | O(n^2) | O(1) | 不稳定 |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | 不稳定 |
- 稳定性
排序前相等的两个元素,排序后相对位置不变
性能测试
import java.util.List;
import java.util.Random;
public class Main {
public static void main(String[] args) {
List<Sort> sortList = List
.of(new BubbleSort3(), new SelectSort(), new InsertSort(),
new ShellSort2(), new MergeSort(), new QuickSort2(), new HeapSort2());
int n = 100000;
int[] originalNums = generateRandomArr(n, n);
for (Sort sort : sortList) {
int[] nums = Arrays.copyOf(originalNums, originalNums.length);
long startTime = System.nanoTime();
sort.sort(nums);
long endTime = System.nanoTime();
System.out.println(sort.getClass().getSimpleName() + " spend time: "
+ (endTime - startTime) / 1_000_000_000f + " s");
checkArrOrder(sort, nums);
}
}
private static int[] generateRandomArr(int n, int bound) {
Random random = new Random();
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = random.nextInt(bound);
}
return arr;
}
private static int[] generateOrderArr(int n) {
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = i;
}
return arr;
}
private static int[] generateReverseOrderArr(int n) {
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = n - i;
}
return arr;
}
private static void checkArrOrder(Sort sort, int[] nums) {
for (int i = 0; i < nums.length - 1; i++) {
if (nums[i] > nums[i + 1]) {
throw new RuntimeException(sort.getClass().getSimpleName() + " arr not order");
}
}
}
}
测试结果为
BubbleSort3 spend time: 15.002914 s
SelectSort spend time: 5.6422544 s
InsertSort spend time: 0.86879486 s
ShellSort2 spend time: 0.0141172 s
MergeSort spend time: 0.0113022 s
QuickSort2 spend time: 0.0142096 s
HeapSort2 spend time: 0.0150131 s








 浙公网安备 33010602011771号
浙公网安备 33010602011771号