java实现AVL树
介绍
AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。示例图如下

整体代码实现
代码基于之前的二叉搜索树实现,java实现二叉搜索树
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
/**
* 自己实现AVL树
*/
public class AVLTree<E extends Comparable<E>> {
/**
* 根节点
*/
private Node<E> root;
/**
* 树的节点数量
*/
private int size;
/**
* 添加元素
*/
public boolean add(E e) {
//从根节点开始查找
Node<E> cur = root;
//带插入节点的父节点
Node<E> parent = null;
int cmp = 0;
while (cur != null) {
cmp = e.compareTo(cur.data);
if (cmp > 0) {
parent = cur;
cur = cur.right;
} else if (cmp < 0) {
parent = cur;
cur = cur.left;
} else {
return false;
}
}
Node<E> node = new Node<>(e);
if (parent == null) {
root = node;
} else {
if (cmp < 0) {
parent.left = node;
} else {
parent.right = node;
}
node.parent = parent;
}
fixAfterUpdate(node);
size++;
return true;
}
/**
* 添加,删除元素之后修复平衡性
*/
private void fixAfterUpdate(Node<E> node) {
Node<E> cur = node;
while (cur != null) {
//必须
updateHeight(cur);
if (balanceFactor(cur) > 1) {
//LL
if (balanceFactor(cur.left) < 0) {
//LR
rotateLeft(cur.left);
}
rotateRight(cur);
} else if (balanceFactor(cur) < -1) {
//RR
if (balanceFactor(cur.right) > 0) {
//RL
rotateRight(cur.right);
}
rotateLeft(cur);
} else {
cur = cur.parent;
}
}
}
private void updateHeight(Node<E> node) {
node.height = Math.max(height(node.left), height(node.right)) + 1;
}
private int balanceFactor(Node<E> node) {
if (node == null) {
return 0;
}
return height(node.left) - height(node.right);
}
private int height(Node<E> node) {
if (node == null) {
return 0;
}
return node.height;
}
// 对节点y进行向右旋转操作
// y x
// / \ / \
// x T4 向右旋转 (y) z y
// / \ - - - - - - - -> / \ / \
// z T3 T1 T2 T3 T4
// / \
// T1 T2
private void rotateRight(Node<E> y) {
Node<E> x = y.left;
Node<E> T3 = x.right;
Node<E> parent = y.parent;
if (parent == null) {
root = x;
} else {
if (y == parent.left) {
parent.left = x;
} else {
parent.right = x;
}
}
x.parent = parent;
x.right = y;
y.parent = x;
y.left = T3;
if (T3 != null) {
T3.parent = y;
}
updateHeight(y);
updateHeight(x);
}
// 对节点y进行向左旋转操作
// y x
// / \ / \
// T4 x 向左旋转 (y) y z
// / \ - - - - - - - -> / \ / \
// T3 z T4 T3 T1 T2
// / \
// T1 T2
private void rotateLeft(Node<E> y) {
Node<E> x = y.right;
Node<E> T3 = x.left;
Node<E> parent = y.parent;
if (parent == null) {
root = x;
} else {
if (y == parent.left) {
parent.left = x;
} else {
parent.right = x;
}
}
x.parent = parent;
y.parent = x;
x.left = y;
y.right = T3;
if (T3 != null) {
T3.parent = y;
}
updateHeight(y);
updateHeight(x);
}
public boolean isBST() {
List<E> res = inOrder();
for (int i = 1; i < res.size(); i++) {
if (res.get(i - 1).compareTo(res.get(i)) > 0) {
return false;
}
}
return true;
}
public boolean isBalanced() {
return isBalanced(root);
}
private boolean isBalanced(Node<E> root) {
if (root == null) {
return true;
}
int balanceFactor = balanceFactor(root);
if (Math.abs(balanceFactor) > 1) {
return false;
}
return isBalanced(root.left) && isBalanced(root.right);
}
/**
* 查询容量
*/
public int size() {
return size;
}
/**
* 是否为空
*/
public boolean isEmpty() {
return size == 0;
}
/**
* 删除指定元素
*/
public boolean remove(E e) {
Node<E> node = find(root, e);
if (node == null) {
return false;
}
fastRemove(node);
size--;
return true;
}
/**
* 在以root为根节点的树中查找值为e的节点
*/
private Node<E> find(Node<E> root, E e) {
if (root != null) {
if (e.compareTo(root.data) > 0) {
return find(root.right, e);
} else if (e.compareTo(root.data) < 0) {
return find(root.left, e);
} else {
return root;
}
}
return root;
}
private void fastRemove(Node<E> node) {
//node为待删除的节点
//将删除一个有左孩子和右孩子的节点的情况转换成删除没有左孩子或没有右孩子的情况
//查找待删除节点的后继节点
if (node.left != null && node.right != null) {
//使用后继节点代替待删除节点
Node<E> successor = minimum(node.right);
node.data = successor.data;
node = successor;
}
Node<E> replacement = (node.left != null) ? node.left : node.right;
if (replacement != null) {
replacement.parent = node.parent;
}
if (node.parent == null) {
//待删除节点没有父节点
root = replacement;
} else {
if (node == node.parent.left) {
node.parent.left = replacement;
} else {
node.parent.right = replacement;
}
}
fixAfterUpdate(node);
node.left = node.right = node.parent = null;
}
private Node<E> minimum(Node<E> root) {
Node<E> cur = root;
while (cur.left != null) {
cur = cur.left;
}
return cur;
}
/**
* 是否包含指定元素
*/
public boolean contains(E e) {
Node<E> node = find(root, e);
return node != null;
}
/**
* 层序遍历
*/
public List<E> levelOrder() {
List<E> res = new ArrayList<>();
Queue<Node<E>> queue = new LinkedList<>();
//将根节点入队
queue.add(root);
while (!queue.isEmpty()) {
Node<E> cur = queue.poll();
if (cur != null) {
//访问当前节点
res.add(cur.data);
//将左孩子入队
queue.add(cur.left);
//将右孩子入队
queue.add(cur.right);
}
}
return res;
}
/**
* 递归实现前序遍历
*/
public List<E> preOrder() {
List<E> res = new ArrayList<>();
preOrder(root, res);
return res;
}
private void preOrder(Node<E> root, List<E> res) {
if (root != null) {
res.add(root.data);
preOrder(root.left, res);
preOrder(root.right, res);
}
}
/**
* 递归实现中序遍历
*/
public List<E> inOrder() {
List<E> res = new ArrayList<>();
inOrder(root, res);
return res;
}
private void inOrder(Node<E> root, List<E> res) {
if (root != null) {
inOrder(root.left, res);
res.add(root.data);
inOrder(root.right, res);
}
}
/**
* 递归实现后序遍历
*/
public List<E> postOrder() {
List<E> res = new ArrayList<>();
postOrder(root, res);
return res;
}
private void postOrder(Node<E> root, List<E> res) {
if (root != null) {
postOrder(root.left, res);
postOrder(root.right, res);
res.add(root.data);
}
}
@Override
public String toString() {
return levelOrder().toString();
}
private static class Node<E> {
/**
* 节点值
*/
E data;
/**
* 节点高度
*/
int height;
/**
* 左孩子
*/
Node<E> left;
/**
* 右孩子
*/
Node<E> right;
/**
* 父节点
*/
Node<E> parent;
Node(E data) {
this.data = data;
}
@Override
public String toString() {
return String.valueOf(data);
}
}
}
平衡修复
二叉搜索树在添加或删除之后可能会出现不平衡的情况,也就是左右孩子的高度差大于1,AVL树多做的就是在添加删除之后修复平衡。不平衡情况一共有4种
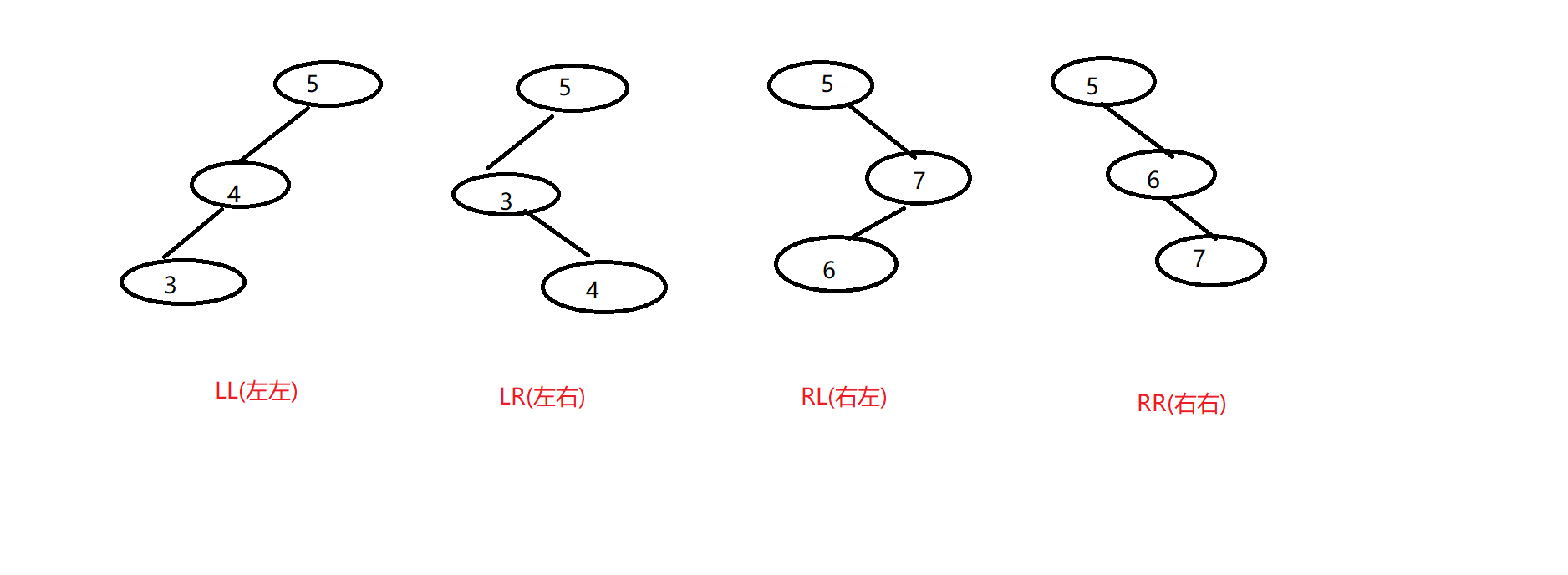
我们只要根据4种情况做处理就可以了
LL(左左)
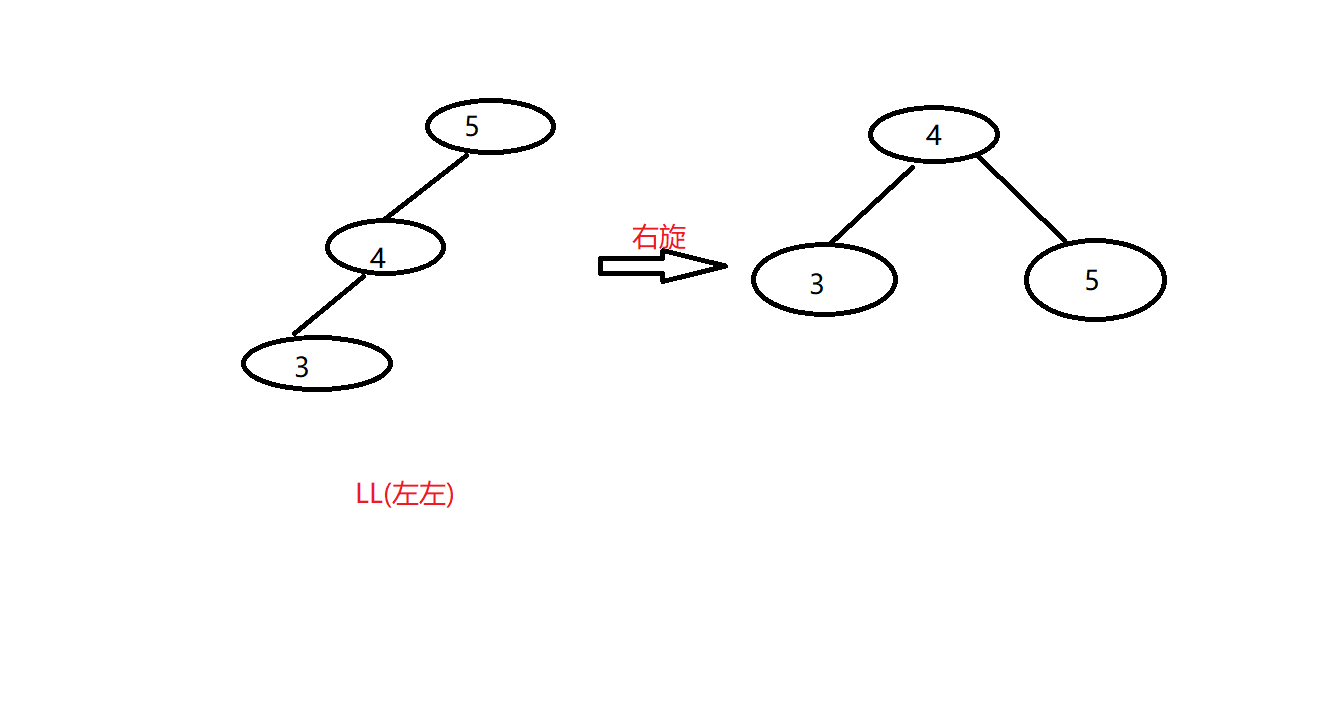
这种情况可以通过右旋转恢复平衡
// 对节点y进行向右旋转操作
// y x
// / \ / \
// x T4 向右旋转 (y) z y
// / \ - - - - - - - -> / \ / \
// z T3 T1 T2 T3 T4
// / \
// T1 T2
private void rotateRight(Node<E> y) {
Node<E> x = y.left;
Node<E> T3 = x.right;
Node<E> parent = y.parent;
if (parent == null) {
root = x;
} else {
if (y == parent.left) {
parent.left = x;
} else {
parent.right = x;
}
}
x.parent = parent;
x.right = y;
y.parent = x;
y.left = T3;
if (T3 != null) {
T3.parent = y;
}
updateHeight(y);
updateHeight(x);
}
LR(左右)
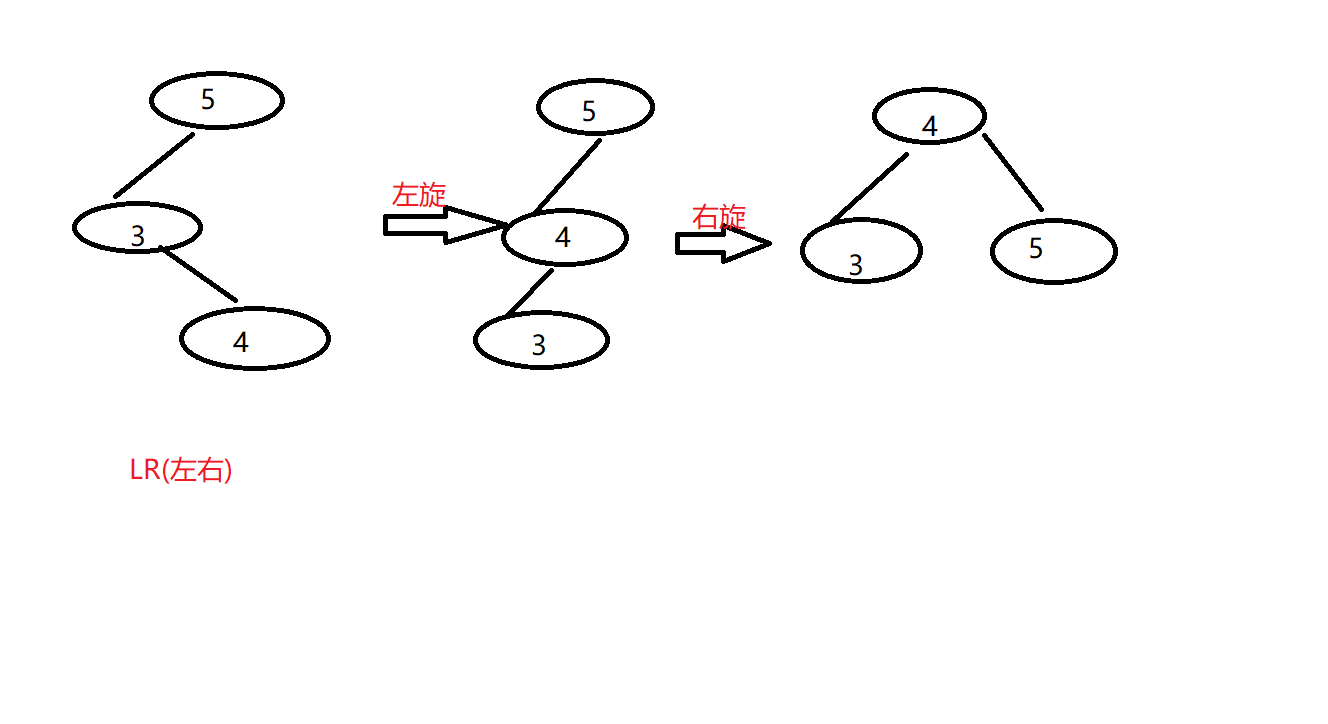
这种情况需要先左旋,变成第一种情况,再右旋。
// 对节点y进行向左旋转操作
// y x
// / \ / \
// T4 x 向左旋转 (y) y z
// / \ - - - - - - - -> / \ / \
// T3 z T4 T3 T1 T2
// / \
// T1 T2
private void rotateLeft(Node<E> y) {
Node<E> x = y.right;
Node<E> T3 = x.left;
Node<E> parent = y.parent;
if (parent == null) {
root = x;
} else {
if (y == parent.left) {
parent.left = x;
} else {
parent.right = x;
}
}
x.parent = parent;
y.parent = x;
x.left = y;
y.right = T3;
if (T3 != null) {
T3.parent = y;
}
updateHeight(y);
updateHeight(x);
}
RL(右左)
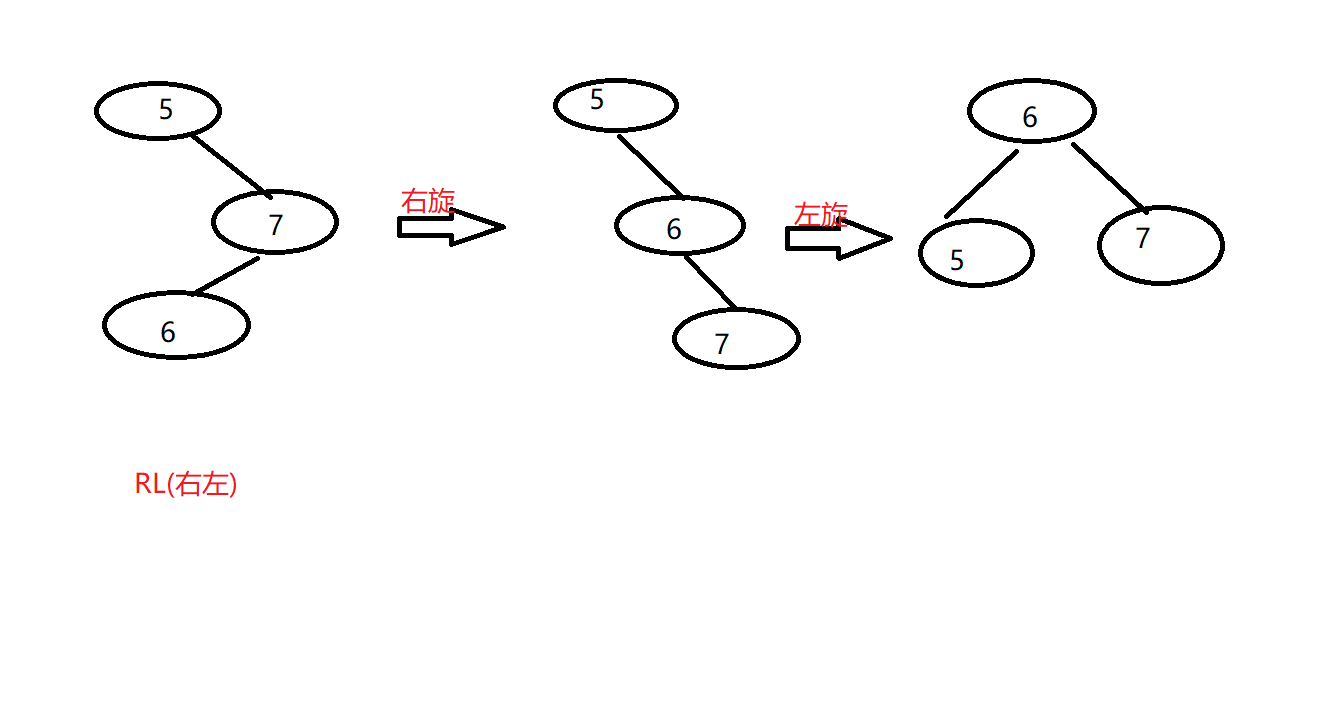
RR(右右)

完整的修复代码
/**
* 添加,删除元素之后修复平衡性
*/
private void fixAfterUpdate(Node<E> node) {
Node<E> cur = node;
while (cur != null) {
//必须
updateHeight(cur);
if (balanceFactor(cur) > 1) {
//LL
if (balanceFactor(cur.left) < 0) {
//LR
rotateLeft(cur.left);
}
rotateRight(cur);
} else if (balanceFactor(cur) < -1) {
//RR
if (balanceFactor(cur.right) > 0) {
//RL
rotateRight(cur.right);
}
rotateLeft(cur);
} else {
cur = cur.parent;
}
}
}
添加元素和删除元素之后都要修复平衡性,从更新的节点开始直到根节点,更新高度。








 浙公网安备 33010602011771号
浙公网安备 33010602011771号