java实现并查集
介绍
并查集是一种特殊的树结构,示例图如下
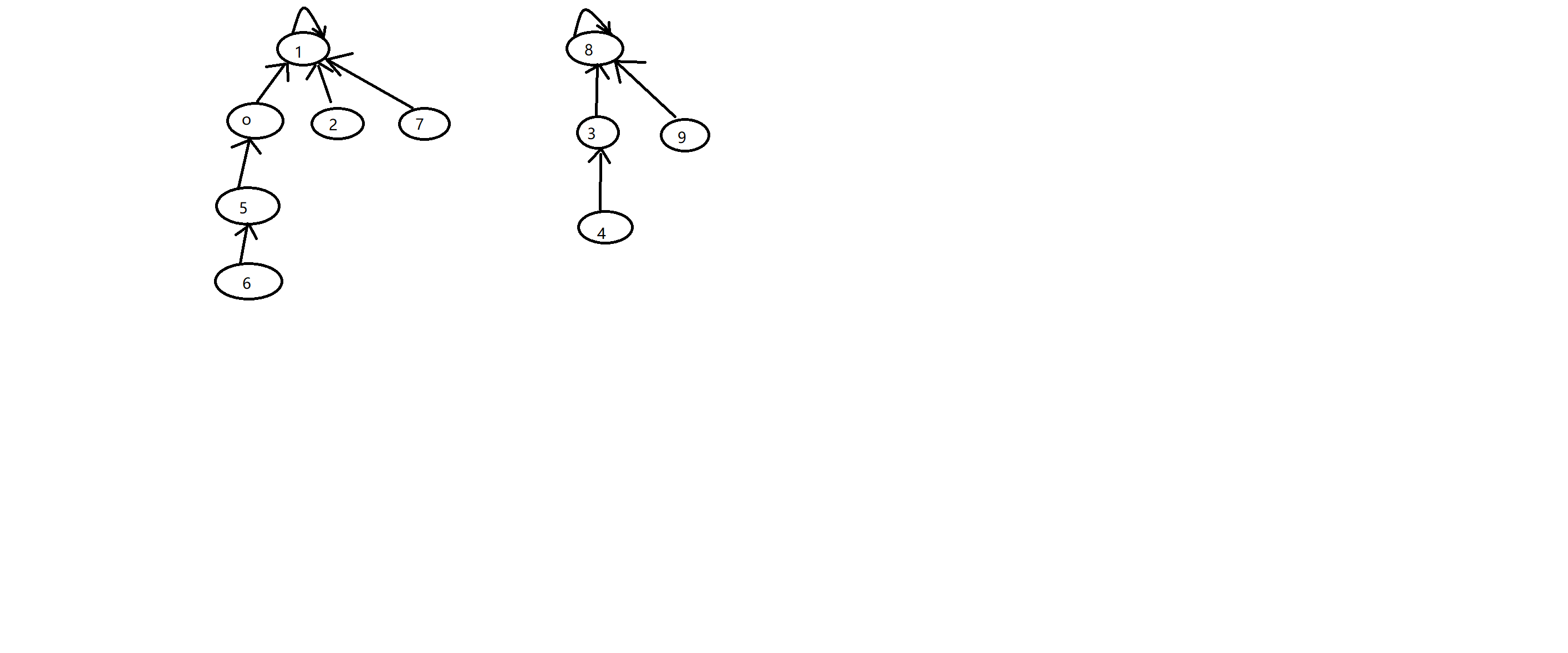
可以很方便的进行以下两种操作:以上图为例
- 判断元素6和元素4是否属于同一组,
- 合并元素6和元素4所在的组
代码实现
public interface UF {
/**
* 容量
*/
int size();
/**
* 是否已连接
*/
boolean connected(int p, int q);
/**
* 合并
*/
void union(int p, int q);
}
定义接口
public class UnionFind implements UF {
private Node[] data;
public UnionFind(int size) {
data = new Node[size];
for (int i = 0; i < data.length; i++) {
//默认每个节点都指向自己
data[i] = new Node(i);
}
}
@Override
public boolean connected(int p, int q) {
rangeCheck(p, q);
return root(p) == root(q);
}
/**
* 查询p指向的根节点
*/
private int root(int p) {
int cur = p;
while (true) {
int parent = data[cur].parent;
if (parent == cur) {
return cur;
}
cur = parent;
}
}
@Override
public void union(int p, int q) {
rangeCheck(p, q);
int pRoot = root(p);
int qRoot = root(q);
if (pRoot == qRoot) {
return;
}
data[qRoot].parent = pRoot;
}
public int size() {
return data.length;
}
private void rangeCheck(int p, int q) {
if (p < 0 || p >= size() || q < 0 || q >= size()) {
throw new IllegalArgumentException("index is illegal");
}
}
private static class Node {
int parent;
Node(int parent) {
this.parent = parent;
}
}
}
测试代码
public class Main {
public static void main(String[] args) {
UF uf = new UnionFind(10);
uf.union(4, 3);
uf.union(3, 8);
uf.union(6, 5);
uf.union(9, 4);
uf.union(2, 1);
uf.union(5, 0);
uf.union(7, 2);
uf.union(6, 2);
System.out.println(uf.connected(0, 2));
System.out.println(uf.connected(0, 7));
System.out.println(uf.connected(3, 9));
System.out.println(uf.connected(6, 4));
}
}
初始化之后的树结构为

每一个父节点都指向自己,经过以上的合并之后的树为
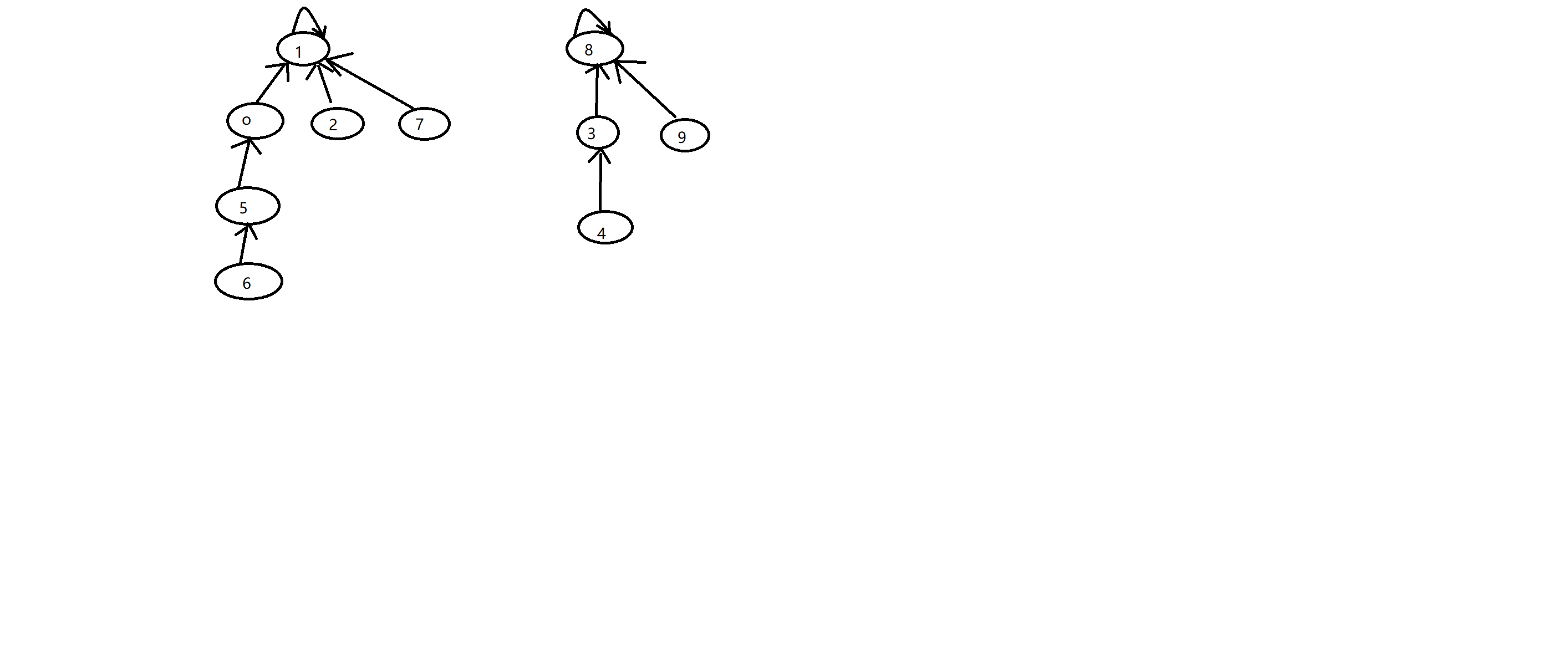
判断两个元素是否连接就是判断两个元素的根节点是否一致。
基于深度的优化
上面的代码虽然功能实现了,但可能出现子链很长的情况,这种情况查询就很低效率。
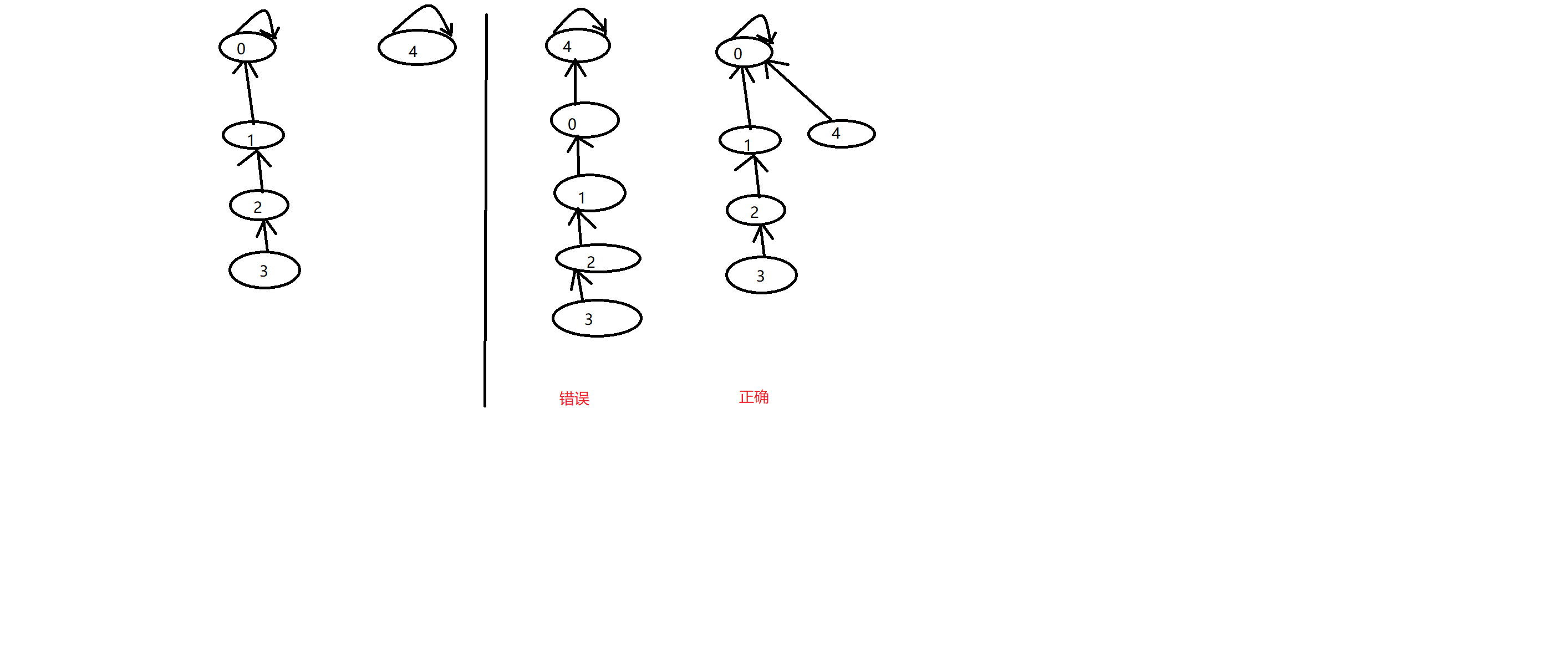
以上图为例,当我们要合并元素3和元素4的时候,我们应该使用后一种合并方式,将深度小的合并到深度大的。
public class UnionFind2 implements UF {
private Node[] data;
public UnionFind2(int size) {
data = new Node[size];
for (int i = 0; i < data.length; i++) {
data[i] = new Node(i, 1);
}
}
@Override
public boolean connected(int p, int q) {
rangeCheck(p, q);
return root(p) == root(q);
}
private int root(int p) {
int cur = p;
while (true) {
int parent = data[cur].parent;
if (parent == cur) {
return cur;
}
cur = parent;
}
}
@Override
public void union(int p, int q) {
rangeCheck(p, q);
int pRoot = root(p);
int qRoot = root(q);
if (pRoot == qRoot) {
return;
}
//深度小的指向深度大的
if (data[pRoot].depth < data[qRoot].depth) {
data[pRoot].parent = qRoot;
} else if (data[pRoot].depth > data[qRoot].depth) {
data[qRoot].parent = pRoot;
} else {
data[pRoot].depth += 1;
}
}
public int size() {
return data.length;
}
private void rangeCheck(int p, int q) {
if (p < 0 || p >= size() || q < 0 || q >= size()) {
throw new IllegalArgumentException("index is illegal");
}
}
private static class Node {
int parent;
int depth;
Node(int parent, int depth) {
this.parent = parent;
this.depth = depth;
}
}
}
路径压缩

在查询的时候我们也可以进行优化
private int root(int p) {
int parent = data[p].parent;
if (parent == p) {
return p;
}
return data[p].parent = root(parent);
}
以查询元素4为例,直接将元素4的父节点指向根节点0。








 浙公网安备 33010602011771号
浙公网安备 33010602011771号