java实现堆数据结构
介绍
堆是一种完全二叉树,最大堆就是每个节点元素的值都要大于其子节点元素的值,相反最小堆就是每个节点元素的值都要小于其子节点元素的值。最小堆示例图如下
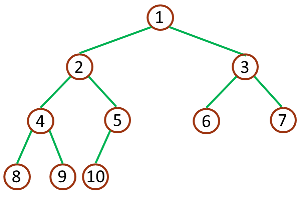
因为完全二叉树的特性,我们可以使用数组来实现堆。
代码实现
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
/**
* 实现一个最大堆
*/
public class MaxHeap<E extends Comparable<E>> {
private List<E> delegate;
public MaxHeap() {
delegate = new ArrayList<>();
}
public MaxHeap(E[] source) {
delegate = new ArrayList<>(Arrays.asList(source));
heapify();
}
/**
* 添加元素
*/
public void add(E e) {
delegate.add(e);
siftUp(size() - 1, e);
}
/**
* 查看最大值元素
*/
public E peek() {
rangeCheck();
return delegate.get(0);
}
/**
* 删除最大值元素
*/
public E poll() {
rangeCheck();
swap(0, size() - 1);
E removeEle = delegate.remove(size() - 1);
siftDown(0);
return removeEle;
}
/**
* 使用新元素替换最大值
*/
public E replace(E e) {
rangeCheck();
E oldEle = delegate.get(0);
delegate.set(0, e);
siftDown(0);
return oldEle;
}
/**
* 将非堆的结构转换成堆结构
*/
private void heapify() {
int size = parent(size() - 1);
for (int i = size; i >= 0; i--) {
siftDown(i);
}
}
/**
* 堆是否为空
*/
public boolean isEmpty() {
return delegate.isEmpty();
}
/**
* 堆容量
*/
public int size() {
return delegate.size();
}
@Override
public String toString() {
return delegate.toString();
}
private void siftUp(int index, E e) {
int cur = index;
while (cur > 0) {
int parentIndex = parent(cur);
E childEle = delegate.get(cur);
E parentEle = delegate.get(parentIndex);
//当前节点大于父节点才交换
if (childEle.compareTo(parentEle) <= 0) {
break;
}
//交换
swap(cur, parentIndex);
cur = parentIndex;
}
}
private void siftDown(int index) {
int size = size();
int cur = index;
while (true) {
int leftIndex = leftChild(cur);
//没有左孩子
if (leftIndex >= size) {
break;
}
int rightIndex = rightChild(cur);
E curEle = delegate.get(cur);
E maxChild = delegate.get(leftIndex);
int maxChildIndex = leftIndex;
//存在右孩子且右孩子大于左孩子
if (rightIndex < size) {
E rightEle = delegate.get(rightIndex);
if (rightEle.compareTo(maxChild) > 0) {
maxChildIndex = rightIndex;
maxChild = rightEle;
}
}
if (maxChild.compareTo(curEle) <= 0) {
break;
}
//将当前节点和左右孩子中的最大节点交换
swap(cur, maxChildIndex);
cur = maxChildIndex;
}
}
private void rangeCheck() {
if (isEmpty()) {
throw new IllegalArgumentException("heap is empty.");
}
}
private void swap(int left, int right) {
E temp = delegate.get(left);
delegate.set(left, delegate.get(right));
delegate.set(right, temp);
}
private int parent(int index) {
return (index - 1) / 2;
}
private int leftChild(int index) {
return index * 2 + 1;
}
private int rightChild(int index) {
return index * 2 + 2;
}
}
堆的核心逻辑就是数据的添加和删除。还是以下图为例
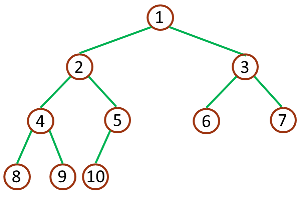
添加元素
这里以添加0为例
- 将元素0添加到最后一个位置,5的右孩子节点
- 将最后一个节点0进行上浮操作,和父节点5比较,小于则交换,循环这个操作,直到根节点
删除元素
这里以删除1为例
- 将最后一个节点10和根节点1交换
- 删除最后一个节点1
- 现在根节点为10,进行下沉操作,和左右孩子中的最小值比较,如果小于就交换,循环这个操作,直到最后一个非叶子节点
优先级队列
根据堆的最大最小特性,我们可以使用堆来实现优先级队列
public interface Queue<E> {
/**
* 队列是否为空
*/
boolean isEmpty();
/**
* 入队
*/
void enqueue(E e);
/**
* 出队
*/
E dequeue();
/**
* 查询队头元素
*/
E peek();
}
定义队列的接口
/**
* 使用堆实现优先级队列
*/
public class PriorityQueue<E extends Comparable<E>> implements Queue<E> {
/**
* 代理对象
*/
private MaxHeap<E> delegate;
public PriorityQueue() {
delegate = new MaxHeap<>();
}
@Override
public boolean isEmpty() {
return delegate.isEmpty();
}
@Override
public void enqueue(E e) {
delegate.add(e);
}
@Override
public E dequeue() {
return delegate.poll();
}
@Override
public E peek() {
return delegate.peek();
}
@Override
public String toString() {
return delegate.toString();
}
}
其实jdk中的优先级队列PriorityQueue也是通过堆来实现的










 浙公网安备 33010602011771号
浙公网安备 33010602011771号