关于数组的算法题（一）

 数组方法：

1、length：

　　　arr.length返回数组长度

 2、Arrays.asList()

　　将数组转化成List集合的方法。

 3、Arrays.fill（）函数

填充a1数组中的每个元素都是value。

Arrays.fill（ a1, value ）;

注：a1是一个数组变量，value是一个a1中元素数据类型的值。

 

1、长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度

最小的连续子数组，并返回其长度。如果不存在符合条件的连续子数组，返回 0。

示例：

输入: s = 7 , n u m s = [ 2 , 3 , 1 , 2 , 4 , 3 ]

输出: 2

解释: 子数组 [ 4 , 3 ] 是该条件下的长度最小的连续子数组。

 

暴力破解法：

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int min = Integer.MAX_VALUE;
        for(int i =0;i<nums.length;i++){
            int sum = nums[i];
            if(sum >= target){
                return 1;
            }
            for(int j = i+1; j<nums.length;j++){
                sum += nums[j];
                if(sum >= target){
                    min = Math.min(min,j-i+1);
                }
            }
        }
        return min == Integer.MAX_VALUE ? 0 : min;
    }
}

 

2、寻找两个正序数组的中位数

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

示例 3：

输入：nums1 = [0,0], nums2 = [0,0]
输出：0.00000

示例 4：

输入：nums1 = [], nums2 = [1]
输出：1.00000

示例 5：

输入：nums1 = [2], nums2 = []
输出：2.00000

 

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int[] nums;
        int m = nums1.length;
        int n = nums2.length;
        nums = new int[m+n];
        if(m == 0){
            if(n % 2 == 0){
                return (nums2[n/2 - 1] + nums2[n/2]) / 2.0;
            }else{
                return nums2[n/2];
            }
        }
        if(n == 0){
            if(m % 2 == 0){
                return (nums1[m/2 - 1] + nums1[m/2]) / 2.0;
            }else{
                return nums1[m/2];
            }
        }
        int count = 0;
        int i = 0;
        int j = 0;
        while(count != (m + n)){
            if(i == m){
                while(j != n){
                    nums[count++] = nums2[j++];
                }
                break;
            }
            if(j == n){
                while(i != m){
                    nums[count++] = nums1[i++];
                }
                break;
            }
            
            if(nums1[i] < nums2[j]){
                nums[count] = nums1[i];
                count++;
                i++;
            }else{
                nums[count] = nums2[j];
                count++;
                j++;
            }
            
        }
        if((m+n) % 2 == 0){
            return (nums[(m+n)/2 - 1] + nums[(m+n) / 2]) / 2.0;
        }else{
            return nums[(m+n) / 2] ;
        }
    }
}

解析：

　　暴力破解法：先将两个数组合并，两个有序数组的合并也是归并排序中的一部分。然后根据奇数，还是偶数，返回中位数。

 

3、数组中重复的数据

给定一个整数数组 a，其中1 ≤ a[i] ≤ n （n为数组长度）, 其中有些元素出现两次而其他元素出现一次。

找到所有出现两次的元素。

示例：

输入:
[4,3,2,7,8,2,3,1]

输出:
[2,3]

class Solution {
    public List<Integer> findDuplicates(int[] nums) {
        List<Integer> res = new ArrayList<>();
        if(nums == null || nums.length == 0){
            return res;
        }
        Set<Integer> set = new HashSet<>();
        for(int n : nums){
            if(!set.add(n)){
                res.add(n);
            }
        }
        return res;
    }
}

 

4、找到所有数组中消失的数字

给你一个含 n 个整数的数组 nums ，其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字，并以数组的形式返回结果。

示例 1：

输入：nums = [4,3,2,7,8,2,3,1]
输出：[5,6]

示例 2：

输入：nums = [1,1]
输出：[2]

class Solution {
    public List<Integer> findDisappearedNumbers(int[] nums) {
        List<Integer> res = new ArrayList<>();
        if(nums == null || nums.length == 0){
            return res;
        }
        int[] tmp = new int[nums.length]; 
        for(int n : nums){
            if(n >= 1 && n <= nums.length){
                tmp[n - 1] = 1;
            }
        }
        for(int i=0;i<nums.length;i++){
            if(tmp[i] == 0){
                res.add(i+1);
            }
        }
        return res;
    }
}

 

5、二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

 

class Solution {
    public int search(int[] nums, int target) {
        if(nums[0] > target || nums[nums.length - 1] < target){
            return -1;
        }
        int left = 0;
        int right = nums.length;
        while(left < right){
            int middle = (left + right) / 2;
            if(nums[middle] > target){
                right = middle;
            }else if(nums[middle] < target){
                left = middle + 1;
            }else{
                return middle;
            }
        }
        return -1;
    }
}

解析：

　　这道题目的前提是数组为有序数组，同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件，当大家看到题目描述满足如上条件的时候，可要想一想是不是可以用二分法了。

二分查找涉及的很多的边界条件，逻辑比较简单，但就是写不好。例如到底是 while(left < right) 还是 while(left <= right)，到底是right = middle呢，还是要right = middle - 1呢？

大家写二分法经常写乱，主要是因为对区间的定义没有想清楚，区间的定义就是不变量。要在二分查找的过程中，保持不变量，就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作，这就是循环不变量规则。

写二分法，区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right)。

下面我用这两种区间的定义分别讲解两种不同的二分写法。

二分法第一种写法

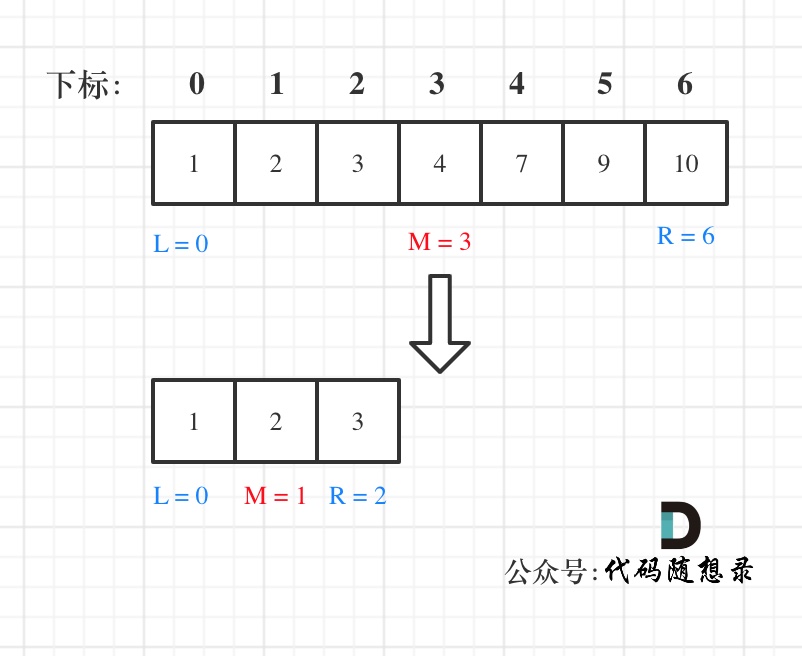
第一种写法，我们定义 target 是在一个在左闭右闭的区间里，也就是[left, right] （这个很重要非常重要）。

区间的定义这就决定了二分法的代码应该如何写，因为定义target在[left, right]区间，所以有如下两点：

• while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
• if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1

例如在数组：1,2,3,4,7,9,10中查找元素2，如图所示：

二分法第二种写法

如果说定义 target 是在一个在左闭右开的区间里，也就是[left, right) ，那么二分法的边界处理方式则截然不同。

有如下两点：

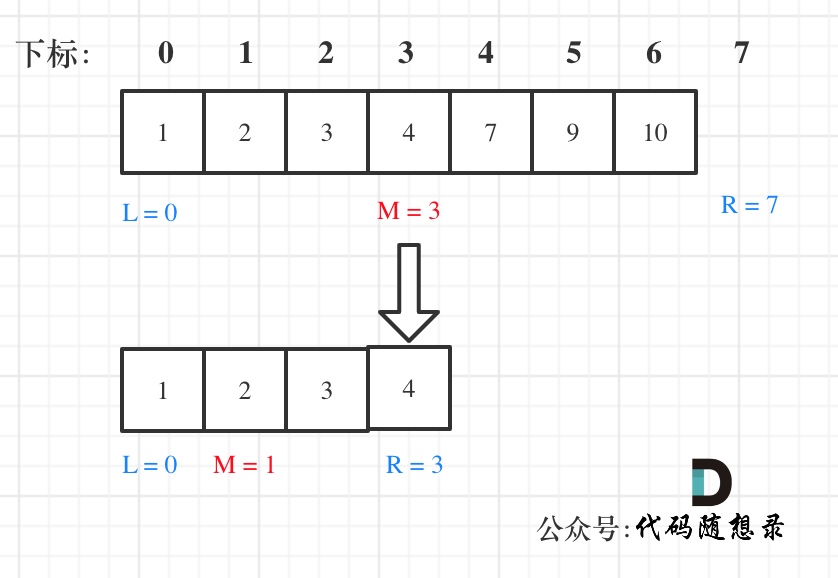
• while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
• if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]

在数组：1,2,3,4,7,9,10中查找元素2，如图所示：（注意和方法一的区别）