[Swift]LeetCode1203. 项目管理 | Sort Items by Groups Respecting Dependencies

★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
➤微信公众号：山青咏芝（let_us_code）
➤博主域名：https://www.zengqiang.org
➤GitHub地址：https://github.com/strengthen/LeetCode
➤原文地址：https://www.cnblogs.com/strengthen/p/11565837.html
➤如果链接不是山青咏芝的博客园地址，则可能是爬取作者的文章。
➤原文已修改更新！强烈建议点击原文地址阅读！支持作者！支持原创！
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★

热烈欢迎，请直接点击！！！

进入博主App Store主页，下载使用各个作品！！！

注：博主将坚持每月上线一个新app！！！

There are n items each belonging to zero or one of m groups where group[i] is the group that the i-th item belongs to and it's equal to -1 if the i-th item belongs to no group. The items and the groups are zero indexed.

Return a sorted list of the items such that:

• The items that belong to the same group are next to each other in the sorted list.
• There are some relations between these items where beforeItems[i] is a list containing all the items that should come before the i-th item in the sorted array (to the left of the i-th item).

Return any solution if there is more than one solution and return an empty list if there is no solution.

 

Example 1:

Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]
Output: [6,3,4,1,5,2,0,7]

Example 2:

Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3],[],[4],[]]
Output: []
Explanation: This is the same as example 1 except that 4 needs to be before 6 in the sorted list.

 

Constraints:

• 1 <= m <= n <= 3*10^4
• group.length == beforeItems.length == n
• -1 <= group[i] <= m-1
• 0 <= beforeItems[i].length <= n-1
• 0 <= beforeItems[i][j] <= n-1
• i != beforeItems[i][j]

---

公司共有 n 个项目和  m 个小组，每个项目要不没有归属，要不就由其中的一个小组负责。

我们用 group[i] 代表第 i 个项目所属的小组，如果这个项目目前无人接手，那么 group[i] 就等于 -1。（项目和小组都是从零开始编号的）

请你帮忙按要求安排这些项目的进度，并返回排序后的项目列表：

• 同一小组的项目，排序后在列表中彼此相邻。
• 项目之间存在一定的依赖关系，我们用一个列表 beforeItems 来表示，其中 beforeItems[i] 表示在进行第 i 个项目前（位于第 i 个项目左侧）应该完成的所有项目。

结果要求：

如果存在多个解决方案，只需要返回其中任意一个即可。

如果没有合适的解决方案，就请返回一个 空列表。

 

示例 1：

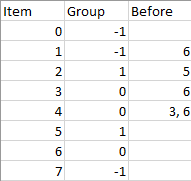
输入：n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]
输出：[6,3,4,1,5,2,0,7]

示例 2：

输入：n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3],[],[4],[]]
输出：[]
解释：与示例 1 大致相同，但是在排序后的列表中，4 必须放在 6 的前面。

 

提示：

• 1 <= m <= n <= 3*10^4
• group.length == beforeItems.length == n
• -1 <= group[i] <= m-1
• 0 <= beforeItems[i].length <= n-1
• 0 <= beforeItems[i][j] <= n-1
• i != beforeItems[i][j]

---

Runtime: 556 ms

Memory Usage: 28.7 MB

class Solution {
    func sortItems(_ n: Int, _ m: Int, _ group: [Int], _ beforeItems: [[Int]]) -> [Int] {
        var group = group
        var ret:[Int] = [Int]()
        //the vector stores the followers of the key which is the group id
        var rules_between_groups:[Int:[Int]] = [Int:[Int]]()
        //the key is the the group id, the value has similar structure as rules_between_groups
        var rules_in_group:[Int:[Int:[Int]]] = [Int:[Int:[Int]]]()
        var mm:Int = m
        for i in 0..<group.count
        {
            //asign group ids for the no-group items
            if group[i] == -1 {group[i] = mm++}
            
        }
        //parse the following/followed (beforeItems) rules
        for i in 0..<beforeItems.count
        {
            for j in 0..<beforeItems[i].count
            {
                if group[beforeItems[i][j]] == group[i]
                {
                    let gg:Int = group[i]
                    rules_in_group[gg,default:[Int:[Int]]()][beforeItems[i][j],default:[Int]()].append(i)
                }
                else
                {
                     rules_between_groups[group[beforeItems[i][j]],default:[Int]()].append(group[i])
                }
            }
        }
        //to remove the duplicated group  id
        var groups:Set<Int> = Set<Int>()
        //key is the group id, vector stores the items
        var items_by_group:[Int:[Int]] = [Int:[Int]]()
        for i in 0..<group.count
        {
            groups.insert(group[i])
            items_by_group[group[i],default:[Int]()].append(i)
        }
        //vector of unique group ids
        var vgroup:[Int] = Array(groups)
        if !applyRules(&vgroup,&rules_between_groups) {return ret}
        for i in 0..<m
        {
            if !applyRules(&items_by_group[i,default:[Int]()], &rules_in_group[i,default:[Int:[Int]]()])
            {
                return ret
            }
        }
        for gg in vgroup
        {
            for ii in items_by_group[gg,default:[Int]()]
            {
                ret.append(ii)
            }
        }
        return ret
    }
    
    func applyRules(_ eles:inout [Int],_ rules:inout [Int:[Int]]) -> Bool
    {
        //toplogical sort
        //id -> indegree number
        var indegree:[Int:Int] = [Int:Int]()
        for ele in eles
        {
            indegree[ele] = 0
        }
        eles.removeAll()
        //calculate the indegrees
        for valu in rules.values
        {
            for i in 0..<valu.count
            {
                indegree[valu[i],default:0] += 1
            }
        }
        while(indegree.count > 0)
        {
            let start:Int = eles.count
            for (key,val) in indegree
            {
                if val == 0
                {
                    eles.append(key)
                    for aa in rules[key,default:[Int]()]
                    {
                        indegree[aa,default:0] -= 1
                    }
                }
            }
            let stop:Int = eles.count
            for i in start..<stop
            {
                indegree[eles[i]] = nil
            }
            if start == stop
            {
                return false
            }
        }
        return true
    }
}

/*扩展Int类，实现自增++、自减--运算符*/
extension Int{
    //后缀++:先执行表达式后再自增
    static postfix func ++(num:inout Int) -> Int {
        //输入输出参数num
        let temp = num
        //num加1
        num += 1
        //返回加1前的数值
        return temp
    }
}