[Swift]LeetCode1135. 最低成本联通所有城市 | Connecting Cities With Minimum Cost
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
➤微信公众号：山青咏芝（shanqingyongzhi）
➤博客园地址：山青咏芝（https://www.cnblogs.com/strengthen/）
➤GitHub地址：https://github.com/strengthen/LeetCode
➤原文地址：https://www.cnblogs.com/strengthen/p/11258422.html
➤如果链接不是山青咏芝的博客园地址，则可能是爬取作者的文章。
➤原文已修改更新！强烈建议点击原文地址阅读！支持作者！支持原创！
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
There are N cities numbered from 1 to N.
You are given connections, where each connections[i] = [city1, city2, cost] represents the cost to connect city1 and city2 together. (A connection is bidirectional: connecting city1 and city2is the same as connecting city2 and city1.)
Return the minimum cost so that for every pair of cities, there exists a path of connections (possibly of length 1) that connects those two cities together. The cost is the sum of the connection costs used. If the task is impossible, return -1.
Example 1:
Input: N = 3, connections = [[1,2,5],[1,3,6],[2,3,1]] Output: 6 Explanation: Choosing any 2 edges will connect all cities so we choose the minimum 2.
Example 2:
Input: N = 4, connections = [[1,2,3],[3,4,4]] Output: -1 Explanation: There is no way to connect all cities even if all edges are used.
Note:
1 <= N <= 100001 <= connections.length <= 100001 <= connections[i][0], connections[i][1] <= N0 <= connections[i][2] <= 10^5connections[i][0] != connections[i][1]
想象一下你是个城市基建规划者，地图上有 N 座城市，它们按以 1 到 N 的次序编号。
给你一些可连接的选项 conections，其中每个选项 conections[i] = [city1, city2, cost] 表示将城市 city1 和城市 city2 连接所要的成本。（连接是双向的，也就是说城市 city1 和城市 city2 相连也同样意味着城市 city2 和城市 city1 相连）。
返回使得每对城市间都存在将它们连接在一起的连通路径（可能长度为 1 的）最小成本。该最小成本应该是所用全部连接代价的综合。如果根据已知条件无法完成该项任务，则请你返回 -1。
示例 1：
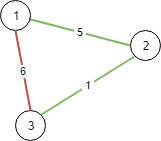
输入：N = 3, conections = [[1,2,5],[1,3,6],[2,3,1]] 输出：6 解释： 选出任意 2 条边都可以连接所有城市，我们从中选取成本最小的 2 条。
示例 2：
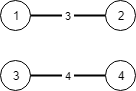
输入：N = 4, conections = [[1,2,3],[3,4,4]] 输出：-1 解释： 即使连通所有的边，也无法连接所有城市。
提示：
1 <= N <= 100001 <= conections.length <= 100001 <= conections[i][0], conections[i][1] <= N0 <= conections[i][2] <= 10^5conections[i][0] != conections[i][1]
